6 20 As A Decimal
saludintensiva
Sep 10, 2025 · 5 min read
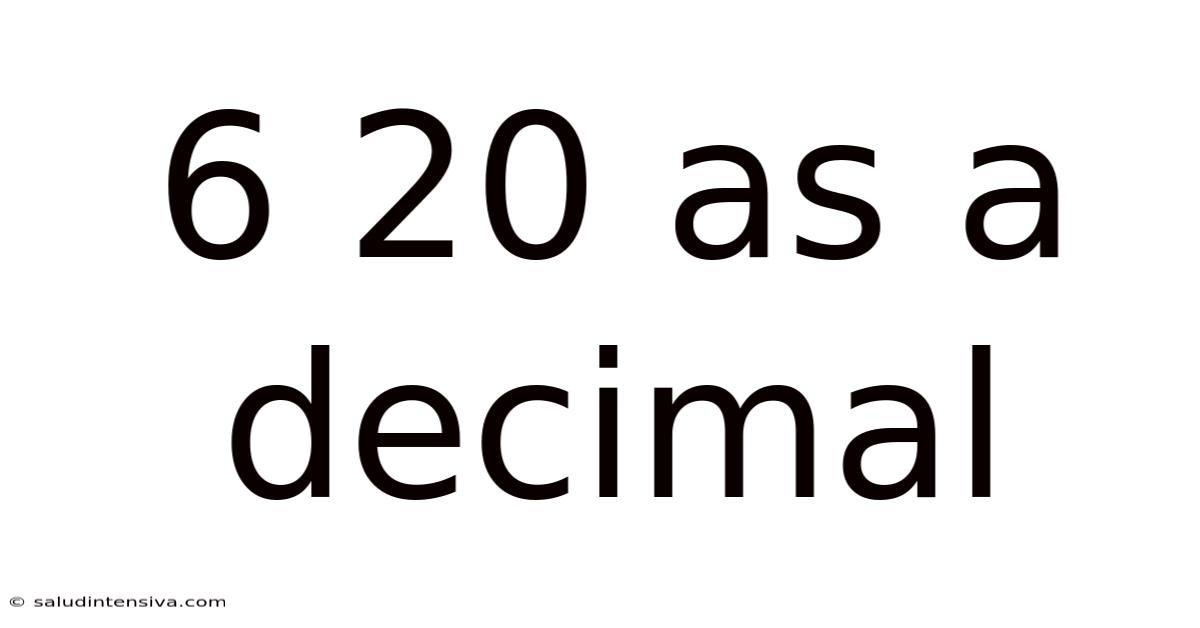
Table of Contents
Understanding 6 20 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics with applications spanning various fields, from everyday calculations to advanced scientific computations. This article delves into the process of converting the mixed number 6 20 into its decimal equivalent, providing a detailed explanation suitable for learners of all levels. We will explore different methods, address common misconceptions, and even touch upon the underlying mathematical principles. Understanding this seemingly simple conversion will solidify your grasp of fractional and decimal representation.
What is a Mixed Number?
Before diving into the conversion, let's clarify the term "mixed number." A mixed number combines a whole number and a proper fraction. In our case, 6 20 represents 6 whole units and 20 of a unit. Understanding this structure is crucial for the conversion process. This representation is commonly used to express quantities that are greater than one but not a whole number.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is arguably the most straightforward approach. We'll break down the conversion into two steps:
-
Convert the fraction to a decimal: To convert the fraction 20 to a decimal, we perform the division 2 ÷ 20. This yields 0.1. You can perform this division using a calculator or by long division. Remember that the numerator (the top number) is divided by the denominator (the bottom number).
-
Add the whole number: Now, simply add the whole number part (6) to the decimal equivalent of the fraction (0.1). This gives us 6 + 0.1 = 6.1.
Therefore, 6 20 as a decimal is 6.1.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves an extra step but demonstrates a deeper understanding of fractional manipulation.
-
Convert to an improper fraction: A mixed number can be converted to an improper fraction (where the numerator is larger than the denominator). To do this, we multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator remains the same.
In our example:
(6 × 20) + 2 = 122
The improper fraction is therefore 122/20.
-
Convert the improper fraction to a decimal: Now, divide the numerator (122) by the denominator (20): 122 ÷ 20 = 6.1.
This method confirms our previous result: 6 20 as a decimal is 6.1.
Understanding the Decimal System
The decimal system, also known as the base-10 system, is a number system that uses ten digits (0-9) to represent all numbers. The position of a digit determines its value. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
The Significance of Place Value
The conversion from a fraction to a decimal hinges on understanding place value. In the decimal 6.1, the digit 6 represents 6 ones (6 x 1), and the digit 1 represents 1 tenth (1 x 0.1 or 1/10). The decimal point precisely delineates the whole numbers from the fractional parts.
Applying the Conversion in Real-World Scenarios
Converting fractions to decimals is essential in numerous real-world situations:
- Financial Calculations: Dealing with money often requires converting fractions of a dollar (cents) to decimals.
- Measurement: Many measurement systems use decimals (e.g., metric system). Converting fractions of units to decimals is necessary for accurate calculations.
- Data Analysis: In statistics and data analysis, fractional data is often converted to decimals for easier computation and interpretation.
- Scientific Applications: Many scientific calculations involve fractional quantities that are readily expressed as decimals.
Common Mistakes and How to Avoid Them
While converting 6 20 to a decimal appears straightforward, some common mistakes can occur:
- Incorrect division: Ensure you divide the numerator by the denominator correctly. Carefully perform the division, either manually or using a calculator.
- Misplacing the decimal point: Pay close attention to the placement of the decimal point. A misplaced decimal point significantly alters the value.
- Confusion with improper fractions: If using the improper fraction method, be meticulous in converting the mixed number to an improper fraction correctly.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert 6 20 to a decimal?
A: Yes, most calculators can handle this conversion directly. Simply enter 6 + (2 ÷ 20) or 122 ÷ 20.
Q: What if the fraction doesn't divide evenly?
A: If the fraction results in a repeating or non-terminating decimal (like 1/3 = 0.333...), you may need to round the decimal to a specific number of decimal places based on the context of the problem.
Q: Are there other methods to convert mixed numbers to decimals?
A: While the methods described above are common and efficient, other approaches exist, particularly involving the use of long division for more complex fractions. The core principle, however, remains the same: converting the fraction to a decimal representation and adding it to the whole number.
Q: Why is understanding this conversion important?
A: This conversion skill is fundamental to numerous mathematical applications and is crucial for handling data in various fields, improving numerical fluency and problem-solving abilities.
Conclusion
Converting the mixed number 6 20 to its decimal equivalent, 6.1, is a straightforward process achievable through multiple methods. By understanding the underlying principles of fractions, decimals, and place value, you can confidently convert any mixed number to its decimal form. Mastering this skill is crucial for success in mathematics and its various applications in the real world. Remember to practice regularly and review the steps to reinforce your understanding and build confidence in your mathematical abilities. Through consistent effort, converting fractions to decimals will become second nature.
Latest Posts
Latest Posts
-
Gcf Of 12 And 28
Sep 10, 2025
-
Mega Millions Random Number Generator
Sep 10, 2025
-
14 3 As A Decimal
Sep 10, 2025
-
What Does 5 3 Equal
Sep 10, 2025
-
Excel Convert Time To Number
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 6 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.