6 5 In Mixed Fraction
saludintensiva
Sep 14, 2025 · 6 min read
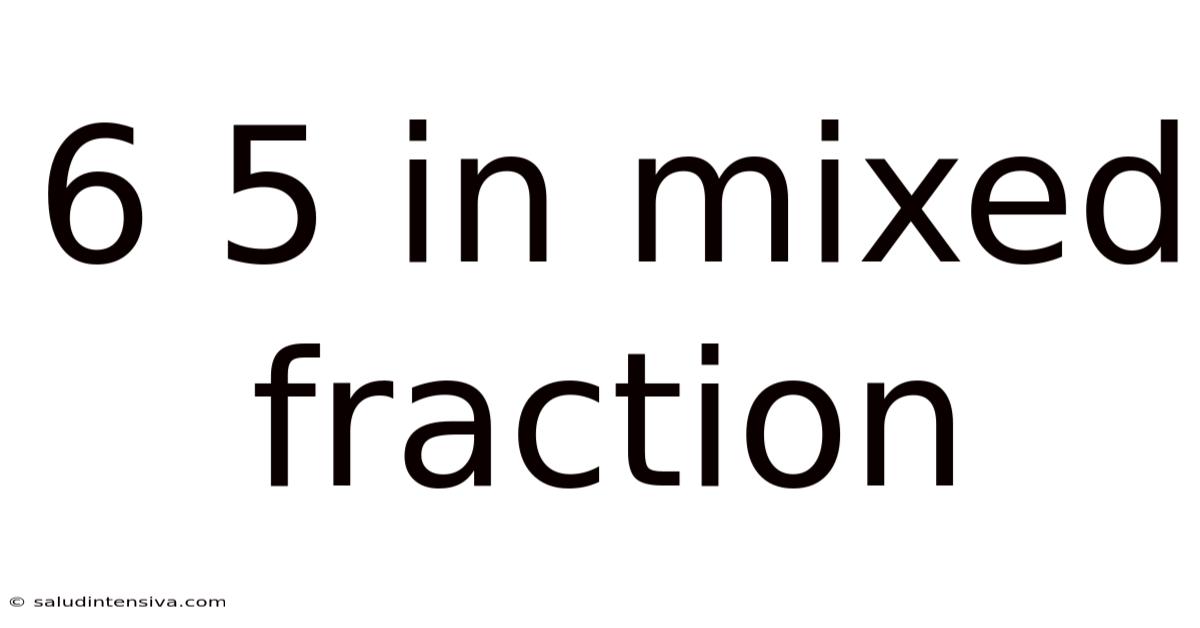
Table of Contents
Decoding the Mystery of 6 5/6: A Deep Dive into Mixed Fractions
Understanding mixed fractions like 6 5/6 is crucial for anyone navigating the world of mathematics, from elementary school students to advanced learners. This comprehensive guide will explore the meaning of 6 5/6, explain how to convert it to an improper fraction and a decimal, delve into its practical applications, and answer frequently asked questions. We’ll cover everything you need to know to confidently tackle this seemingly simple, yet fundamentally important, mathematical concept.
What is a Mixed Fraction?
A mixed fraction combines a whole number and a proper fraction. It represents a quantity that is greater than one. The number to the left of the space is the whole number, and the fraction to the right represents a part of a whole. In our example, 6 5/6, the '6' represents six whole units, and the '5/6' represents five-sixths of another unit. Think of it like having six whole pizzas and five-sixths of another pizza.
Understanding 6 5/6
Let's break down 6 5/6 piece by piece. The whole number, 6, signifies six complete units. The fraction 5/6 represents five parts out of a possible six equal parts of a single unit. This means we're dealing with a quantity slightly less than seven whole units. This understanding forms the basis for all further calculations and conversions involving this mixed fraction.
Converting 6 5/6 to an Improper Fraction
An improper fraction is a fraction where the numerator (top number) is greater than or equal to the denominator (bottom number). Converting a mixed fraction to an improper fraction is a fundamental skill in mathematics. Here's how to convert 6 5/6:
- Multiply the whole number by the denominator: 6 * 6 = 36
- Add the numerator to the result: 36 + 5 = 41
- Keep the same denominator: The denominator remains 6.
Therefore, 6 5/6 is equivalent to the improper fraction 41/6. This representation is useful in many mathematical operations, particularly multiplication and division of fractions.
Converting 6 5/6 to a Decimal
Converting a mixed fraction to a decimal involves a two-step process:
- Convert to an improper fraction: As shown above, 6 5/6 converts to 41/6.
- Divide the numerator by the denominator: Divide 41 by 6. This will result in a decimal number.
41 ÷ 6 = 6.8333...
Therefore, 6 5/6 is approximately equal to 6.833. The decimal representation is often preferred in contexts where precision is crucial, such as scientific calculations or engineering applications. Note that the '3' repeats infinitely, indicating a recurring decimal.
Practical Applications of Mixed Fractions
Mixed fractions find widespread applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. A recipe might call for 2 1/2 cups of flour or 1 3/4 teaspoons of baking powder. Understanding mixed fractions is crucial for accurate measurement and successful cooking.
-
Measurement and Construction: In construction and carpentry, measurements are frequently expressed using mixed fractions. For instance, a piece of wood might measure 5 3/8 inches or a wall might be 8 1/2 feet high.
-
Time Management: Time is often represented using mixed fractions. For instance, a project might take 2 1/2 hours to complete, or a race might last 1 3/4 hours.
-
Finance and Accounting: In financial calculations, particularly those involving fractions of shares or percentages, mixed fractions can simplify representation and calculations.
-
Data Analysis and Statistics: Mixed fractions can occur in data sets, and understanding their representation is important for accurate analysis and interpretation.
Working with 6 5/6: Addition, Subtraction, Multiplication, and Division
To work with mixed fractions like 6 5/6 effectively, it's usually easiest to convert them to improper fractions first, perform the operation, and then convert back to a mixed fraction if needed.
Addition: To add mixed fractions, convert them to improper fractions, find a common denominator, add the numerators, and then simplify the result.
Subtraction: Similar to addition, convert to improper fractions, find a common denominator, subtract the numerators, and simplify.
Multiplication: Convert mixed fractions to improper fractions, multiply the numerators, multiply the denominators, and simplify.
Division: Convert mixed fractions to improper fractions, invert the second fraction (reciprocal), multiply the numerators and denominators, and simplify.
Advanced Concepts: Simplifying and Reducing Fractions
While 6 5/6 is already in its simplest form, understanding simplification is crucial. A fraction is simplified when the greatest common divisor (GCD) of the numerator and denominator is 1. For example, 12/18 simplifies to 2/3 because the GCD of 12 and 18 is 6.
Frequently Asked Questions (FAQ)
Q: What is the difference between a mixed fraction and an improper fraction?
A: A mixed fraction consists of a whole number and a proper fraction, while an improper fraction has a numerator greater than or equal to its denominator.
Q: Can all improper fractions be converted to mixed fractions?
A: Yes, all improper fractions can be converted to mixed fractions by dividing the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction part.
Q: How do I compare two mixed fractions?
A: Convert both mixed fractions to improper fractions and then compare them by comparing their numerators. The fraction with the larger numerator is the greater fraction.
Q: Are there any real-world examples where 6 5/6 might be used?
A: Imagine measuring the length of a piece of lumber. It might measure 6 and 5/6 feet long. Or, perhaps you're calculating the amount of time spent on a project, and you've worked for 6 and 5/6 hours.
Q: What if the denominator is a large number? Does the process change?
A: No, the process of converting between mixed fractions and improper fractions remains the same regardless of the size of the denominator. The calculations might be more complex, but the fundamental steps remain consistent.
Conclusion: Mastering Mixed Fractions
Understanding mixed fractions is a cornerstone of mathematical literacy. From everyday tasks like cooking to complex engineering calculations, the ability to work confidently with mixed fractions, converting them to improper fractions and decimals, and performing arithmetic operations on them, is invaluable. By mastering this concept, you'll unlock a deeper understanding of fractions and their applications in numerous fields. Remember to practice regularly and apply your knowledge in real-world scenarios to reinforce your understanding. This will enable you to approach more advanced mathematical concepts with greater confidence and ease. The seemingly simple 6 5/6 holds a world of mathematical possibilities waiting to be explored!
Latest Posts
Latest Posts
-
2 C 10 C 3
Sep 14, 2025
-
Magnitude Of Resultant Force Calculator
Sep 14, 2025
-
What Are Multiples Of 12
Sep 14, 2025
-
How Long Is 228 Minutes
Sep 14, 2025
-
1 7 M Height In Feet
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6 5 In Mixed Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.