6.5 Percent As A Decimal
saludintensiva
Sep 22, 2025 · 5 min read
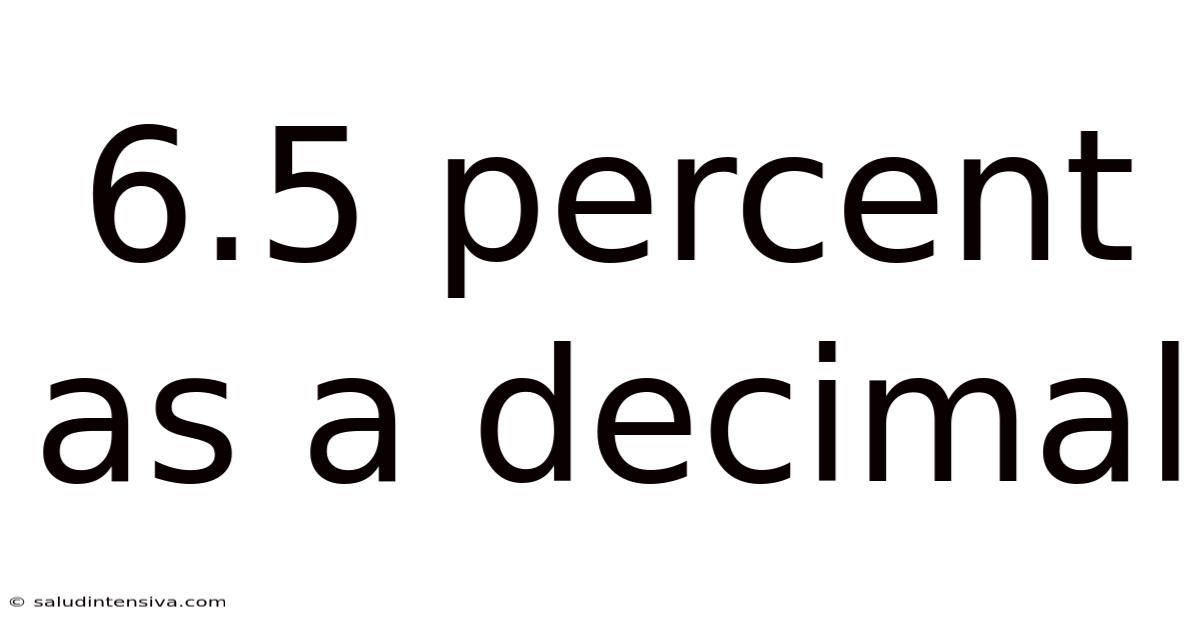
Table of Contents
6.5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and has wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending financial statements and statistical data. This comprehensive guide will delve into the conversion of 6.5 percent to its decimal form, explaining the process step-by-step and exploring its practical implications. We will also examine related concepts and answer frequently asked questions to ensure a thorough understanding of this important mathematical concept.
Understanding Percentages and Decimals
Before we dive into converting 6.5 percent to a decimal, let's establish a clear understanding of both concepts. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. Decimals are essential for representing fractions and percentages in a way that's easily understood and used in calculations.
Converting 6.5 Percent to a Decimal: The Process
The conversion of a percentage to a decimal is straightforward. The key is to remember that a percentage is a fraction with a denominator of 100. Therefore, to convert a percentage to a decimal, you simply divide the percentage by 100.
Here's how to convert 6.5% to a decimal:
-
Write the percentage as a fraction: 6.5% can be written as 6.5/100.
-
Divide the numerator by the denominator: 6.5 ÷ 100 = 0.065
Therefore, 6.5% as a decimal is 0.065.
Alternative Method: Moving the Decimal Point
A quicker method involves moving the decimal point two places to the left. This works because dividing by 100 is equivalent to moving the decimal point two places to the left. In the case of 6.5%, we move the decimal point (implicitly located after the 5) two places to the left:
6.5% becomes 0.065
This method is particularly useful for mental calculations and quick conversions.
Practical Applications of 6.5% as a Decimal (0.065)
Understanding the decimal equivalent of 6.5% has numerous practical applications across various fields:
-
Finance: Calculating simple interest, compound interest, discounts, taxes, and profit margins often involves converting percentages to decimals. For instance, if a bank offers a 6.5% annual interest rate on a savings account, you would use 0.065 to calculate the interest earned.
-
Statistics: Percentages and decimals are fundamental in statistical analysis. Representing data as decimals facilitates calculations such as calculating means, standard deviations, and probabilities. For example, if 6.5% of a sample population exhibits a certain characteristic, this would be represented as 0.065 in statistical analyses.
-
Business: Calculating sales tax, markups, and discounts requires converting percentages to decimals. Understanding these conversions helps businesses accurately price goods and services, track profits, and manage expenses. A 6.5% sales tax, for instance, would be applied using the decimal 0.065.
-
Science: Many scientific calculations involve percentages and their decimal equivalents. For instance, expressing concentrations of solutions or analyzing experimental data often utilizes decimal representation of percentages. A 6.5% solution of a particular substance would be represented by 0.065 in the context of a chemical formula or scientific study.
Understanding the Significance of the Decimal Place Value
It is crucial to understand the significance of the digits in the decimal 0.065.
- 0: Represents the whole number part (there are no whole units).
- 0: Represents the tenths place (no tenths).
- 6: Represents the hundredths place (six hundredths).
- 5: Represents the thousandths place (five thousandths).
This shows that 0.065 is equivalent to 65/1000, further emphasizing the connection between decimals, fractions, and percentages.
Working with 6.5% in Calculations
Let's illustrate the practical use of 0.065 in a few examples:
-
Calculating a discount: If an item is priced at $100 and is discounted by 6.5%, the discount amount is calculated as follows: $100 * 0.065 = $6.50. The final price would be $100 - $6.50 = $93.50.
-
Calculating interest: If you deposit $1000 in a savings account with a 6.5% annual interest rate, the interest earned after one year would be: $1000 * 0.065 = $65.
-
Calculating tax: If the sales tax is 6.5%, the tax on an item costing $50 would be: $50 * 0.065 = $3.25.
Frequently Asked Questions (FAQ)
-
Q: Can I convert a percentage with a decimal directly to a decimal?
- A: Yes, the process remains the same. You still divide the percentage by 100 or move the decimal point two places to the left.
-
Q: What if the percentage is a whole number (e.g., 10%)?
- A: The same rules apply. 10% becomes 10/100 = 0.10 or simply 0.1.
-
Q: How do I convert a decimal back to a percentage?
- A: Multiply the decimal by 100 and add the percent sign (%). For example, 0.065 * 100 = 6.5%, demonstrating the reversible nature of the conversion.
-
Q: Are there any other ways to represent 6.5%?
- A: Yes, you can represent it as a fraction (65/1000), a ratio (65:1000), or as a proportion (0.065).
-
Q: Why is understanding percentage to decimal conversion important?
- A: It's essential for accurate calculations in various fields, ensuring correct interpretation of data and facilitating efficient problem-solving.
Conclusion
Converting 6.5 percent to its decimal equivalent, 0.065, is a crucial skill with widespread practical applications. Understanding this conversion, along with the underlying principles of percentages and decimals, empowers individuals to confidently tackle mathematical problems in diverse contexts, from personal finance to scientific research. By mastering this fundamental concept, you equip yourself with a valuable tool for navigating the numerical world efficiently and accurately. Remember that the seemingly simple act of converting a percentage to a decimal opens doors to a deeper understanding of numerical relationships and their practical implications in various aspects of life.
Latest Posts
Latest Posts
-
1 3 Of A Foot
Sep 22, 2025
-
What Is A Rate Ratio
Sep 22, 2025
-
What Is A Nonzero Digit
Sep 22, 2025
-
What Is 2 25 Equal To
Sep 22, 2025
-
3 8 1 2 Reducer
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 6.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.