6 7 X 6 7
saludintensiva
Sep 25, 2025 · 6 min read
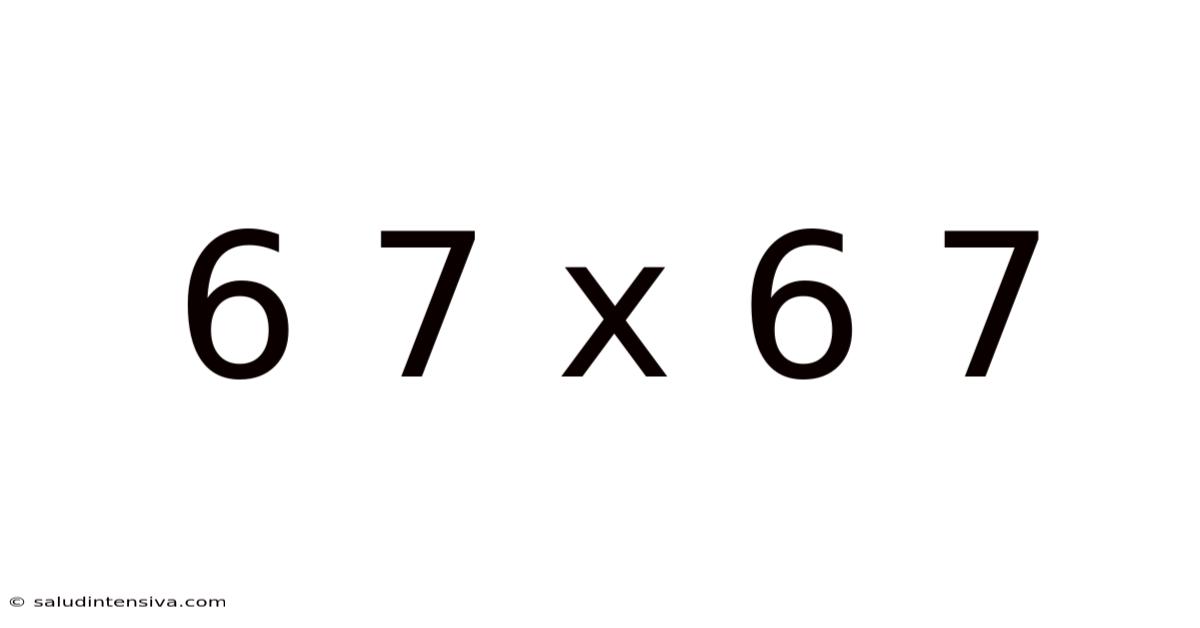
Table of Contents
Decoding 67 x 67: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem of 67 x 67, but delves far beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and even some fascinating historical context. Understanding this seemingly basic calculation opens doors to a broader comprehension of arithmetic, algebra, and even advanced mathematical concepts. We'll cover various methods for solving this problem, explore the reasons behind its seemingly arbitrary nature, and demonstrate its relevance in real-world scenarios.
The Fundamentals: Understanding Multiplication
Before we tackle 67 x 67, let's refresh the fundamentals of multiplication. Multiplication is essentially repeated addition. For example, 3 x 4 means adding three four times (4 + 4 + 4 = 12), or adding four three times (3 + 3 + 3 + 3 = 12). This seemingly simple concept forms the foundation of countless mathematical operations. Understanding this fundamental concept is crucial before we delve into more complex calculations.
Method 1: The Standard Algorithm
The most common method for solving 67 x 67 is the standard algorithm taught in schools. This involves multiplying the units digit first, then the tens digit, and finally adding the results.
- Multiply the units digit: 7 x 7 = 49. Write down '9' and carry-over '4'.
- Multiply the tens digit by the units digit (and add the carry-over): (6 x 7) + 4 = 46. Write down '6' and carry-over '4'.
- Multiply the tens digit by the tens digit (and add the carry-over): (6 x 6) + 4 = 40. Write down '40'.
- Combine the results: 4069.
Therefore, 67 x 67 = 4489.
This method, while straightforward, relies on memorization of multiplication tables and a step-by-step process. While effective, it doesn’t necessarily illuminate the underlying mathematical structure.
Method 2: The Distributive Property (FOIL Method)
A more insightful approach uses the distributive property, often visualized with the FOIL method (First, Outer, Inner, Last) when working with binomials in algebra. We can represent 67 as (60 + 7). Therefore, 67 x 67 becomes:
(60 + 7) x (60 + 7)
Applying the distributive property:
- First: 60 x 60 = 3600
- Outer: 60 x 7 = 420
- Inner: 7 x 60 = 420
- Last: 7 x 7 = 49
Adding these results together: 3600 + 420 + 420 + 49 = 4489
This method not only provides the correct answer but also demonstrates the fundamental algebraic principle of the distributive property, which is crucial in higher-level mathematics.
Method 3: Difference of Squares
This method leverages the algebraic identity a² - b² = (a + b)(a - b). While it might seem counterintuitive at first, we can adapt this to our problem by considering the numbers surrounding 67.
Let's consider 67 as the average of 66 and 68. We can rewrite the equation as:
[(68 - 1) x (68 - 1)]
Expanding this using the formula (a-b)² = a² - 2ab + b² where a = 68 and b = 1:
68² - 2(68)(1) + 1² = 4624 - 136 + 1 = 4489
While this method may appear more complex for this specific problem, understanding the concept of difference of squares is invaluable in solving more intricate algebraic equations and understanding quadratic expressions.
Method 4: Using a Calculator
In the modern era, calculators provide a quick and efficient method for solving multiplication problems. Simply input "67 x 67" and the calculator will instantly provide the answer: 4489. While convenient, relying solely on calculators can hinder the development of fundamental mathematical skills and understanding.
The Significance of 67 x 67: Beyond the Calculation
The seemingly simple calculation of 67 x 67 offers more than just a numerical answer. It provides a practical illustration of several core mathematical concepts:
- The commutative property of multiplication: The order of the numbers doesn't affect the outcome (67 x 67 = 67 x 67).
- The associative property of multiplication: Grouping of numbers doesn't affect the outcome (when multiplying multiple numbers).
- The distributive property: Crucial for expanding algebraic expressions and simplifying equations.
- The concept of squares: 67 x 67 represents 67 squared (67²), illustrating the geometric interpretation of squaring a number.
These concepts extend beyond simple multiplication and form the bedrock of more advanced mathematical topics like algebra, calculus, and beyond.
Real-World Applications
While the calculation itself might seem abstract, multiplication is vital in numerous real-world scenarios:
- Calculating areas: Determining the area of a square or rectangle (e.g., flooring, painting, land surveying).
- Financial calculations: Computing interest, calculating total costs, budgeting, and investments.
- Engineering and physics: Solving problems involving force, acceleration, and various other physical quantities.
- Data analysis: Working with large datasets, scaling data, calculating averages, and determining statistical significance.
- Computer programming: Multiplication operations are fundamental in numerous algorithms and programming tasks.
Even simple calculations like 67 x 67 demonstrate the interconnectedness of mathematics to various practical aspects of everyday life and professional fields.
Historical Context: The Evolution of Multiplication Methods
The methods of multiplication haven't always been as straightforward as they are today. Ancient civilizations used various ingenious techniques, often involving different number systems and visual aids. Understanding the historical context reveals the evolution of mathematical thinking and the gradual refinement of calculation methods over centuries. From the use of abacuses to the development of algorithms, the journey towards efficient multiplication techniques is a testament to human ingenuity.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when multiplying numbers like 67 x 67?
A: Common mistakes include errors in carrying over digits, misplacing digits during the addition step, and forgetting to account for the place value of each digit. Carefully following the steps of the standard algorithm and using visual aids (like grid multiplication) can help minimize errors.
Q: Are there other methods to calculate 67 x 67?
A: Yes, there are numerous methods, some more efficient than others depending on the numbers involved. Methods like lattice multiplication, using logarithms (for larger numbers), and mental math techniques can all be employed.
Q: Why is it important to learn different multiplication methods?
A: Learning different methods enhances mathematical understanding, develops problem-solving skills, and provides alternative approaches when one method might be less efficient than another. It also fosters deeper understanding of underlying mathematical principles.
Conclusion: The Enduring Power of Simple Calculations
While the problem of 67 x 67 might appear simple at first glance, a deeper exploration unveils a wealth of mathematical concepts and practical applications. From the fundamental principles of multiplication to the application of algebraic identities and the historical context of calculation methods, this seemingly basic problem offers a window into the broader world of mathematics and its significance in our everyday lives. Mastering this fundamental skill not only provides the answer to a specific problem but also cultivates a stronger foundation for more complex mathematical challenges and real-world applications. The ability to understand and solve such problems is essential for success in various academic disciplines and professional careers. The simple act of multiplying 67 by 67 underscores the enduring power of fundamental mathematical principles.
Latest Posts
Latest Posts
-
18 X 32 Picture Frame
Sep 25, 2025
-
Yard To Meter Conversion Swimming
Sep 25, 2025
-
Convert 14 Millimeters To Inches
Sep 25, 2025
-
3 8 R 2 3
Sep 25, 2025
-
50 Vietnamese Dong To Usd
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 6 7 X 6 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.