6x 4x 6 24 9x
saludintensiva
Sep 23, 2025 · 5 min read
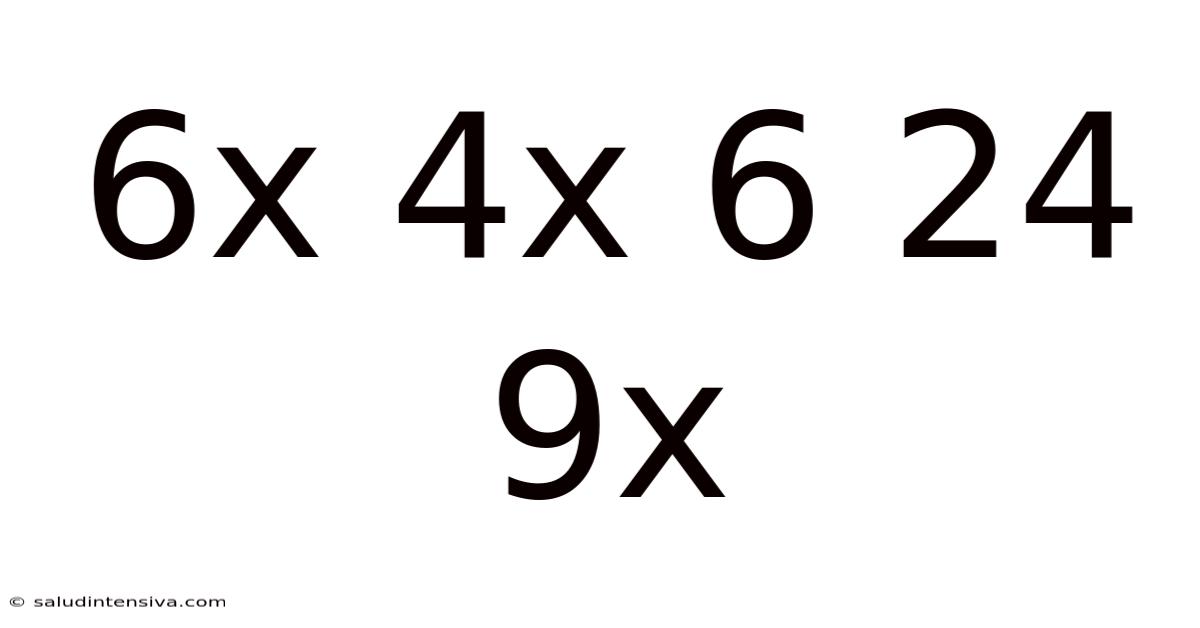
Table of Contents
Decoding the Sequence: Unveiling the Pattern in "6x 4x 6 24 9x"
This article delves into the intriguing numerical sequence "6x 4x 6 24 9x," exploring potential patterns, mathematical operations, and logical reasoning to determine the missing value represented by 'x'. We'll examine various approaches, from simple arithmetic to more complex mathematical concepts, aiming to find a solution that's both mathematically sound and logically consistent. Understanding sequences like this is fundamental to developing crucial problem-solving skills in mathematics and beyond. This exploration will provide a detailed, step-by-step analysis, suitable for anyone curious about mathematical puzzles and pattern recognition.
Understanding the Problem: Initial Observations
The sequence "6x 4x 6 24 9x" presents a challenge: finding the value of 'x' that satisfies a consistent mathematical relationship between the numbers. At first glance, the sequence seems random. However, a closer examination reveals potential underlying patterns that we can investigate. The presence of the 'x' symbol suggests that the missing numbers are not arbitrarily chosen, but rather follow a specific rule or formula. Our goal is to identify this rule.
Method 1: Exploring Arithmetic Operations
Let's start by investigating simple arithmetic operations: addition, subtraction, multiplication, and division. We can try different combinations to see if a consistent pattern emerges.
- Addition/Subtraction: Adding or subtracting consecutive numbers doesn't seem to produce a consistent result.
- Multiplication/Division: A more promising approach is to examine multiplication and division. Notice that 6 multiplied by 4 equals 24. This suggests a potential pattern involving multiplication. However, simply multiplying consecutive numbers doesn't consistently lead to the next number in the sequence.
Method 2: Identifying a Potential Pattern
Let's analyze the relationships between consecutive pairs of numbers. Consider the following:
- 6 and 4: The relationship between 6 and 4 is not immediately obvious through simple arithmetic.
- 4 and 6: Similarly, the relationship between 4 and 6 isn't clearly defined by basic operations.
- 6 and 24: This pair shows a clear relationship: 6 multiplied by 4 equals 24.
- 24 and 9: This pair seems to lack a direct relationship through simple multiplication or division.
This highlights that a single arithmetic operation might not be sufficient to explain the entire sequence. We might need to consider more complex operations or a combination of operations.
Method 3: Introducing the Concept of Sequences and Series
The sequence "6x 4x 6 24 9x" can be viewed as a mathematical sequence. Mathematical sequences are ordered lists of numbers that follow a specific pattern or rule. The challenge is to identify the rule governing this particular sequence. There are various types of sequences, including arithmetic sequences (where the difference between consecutive terms is constant) and geometric sequences (where the ratio between consecutive terms is constant). This sequence doesn't fit neatly into either category.
Let's consider the possibility of a more complex relationship involving multiple steps or operations. We might need to consider:
- Alternating operations: Perhaps the sequence involves alternating between different operations (e.g., multiplication, division, addition, or subtraction).
- Hidden patterns: There might be a hidden pattern within the sequence that is not immediately apparent.
- Modular arithmetic: Advanced mathematical concepts such as modular arithmetic might be necessary to uncover the pattern.
Method 4: A Step-by-Step Deductive Approach
Let's attempt a more methodical approach. We know that 6 multiplied by 4 equals 24. This suggests that multiplication plays a crucial role. Let's consider the possibility of a pattern where we alternate between operations, potentially involving multiplication and a yet-to-be-determined operation.
- 6 x 4 = 24: This establishes a clear multiplicative relationship.
- Consider the relationship between 24 and 9: There isn't an obvious relationship through simple multiplication or division. Let's explore other possibilities.
We need to identify a mathematical operation that would transform 24 into a number that can be meaningfully related to 9. One possibility is to consider a division operation or a combination of operations involving addition or subtraction. Let's explore this further.
Let's assume there's a subtractive element within the sequence. If we subtract a number from 24 to get a number that is a multiple of 9, we can potentially discover a pattern.
Consider the equation 24 - x = 9y, where 'x' is an unknown number and 'y' is an integer. We want to find a suitable 'x' that makes the equation true and produces a consistent pattern.
By solving this equation, we could potentially find a solution that reveals the underlying structure of the sequence.
Method 5: Exploring the Role of 'x'
The inclusion of 'x' in the sequence is critical. The 'x' doesn't necessarily represent a single number. It could represent a variable within a mathematical function or formula. The pattern could involve a relationship between the numbers and their positions in the sequence.
Let's try to establish a relationship between the numbers in the sequence and their positions (1st, 2nd, 3rd, 4th, 5th). We can label them as follows:
- a₁ = 6
- a₂ = 4
- a₃ = 6
- a₄ = 24
- a₅ = 9
Trying to define a simple function that relates these numbers and their positions might reveal the pattern.
Method 6: Considering the Context
Without additional information or context, definitively solving the sequence is challenging. The sequence itself might be part of a larger problem or context. For instance, it could be a puzzle that requires further information.
Conclusion: The Importance of Pattern Recognition
Solving mathematical sequences like "6x 4x 6 24 9x" requires a combination of intuition, mathematical knowledge, and systematic exploration. While we haven't arrived at a definitive solution without further information or context, the analysis illustrates the importance of pattern recognition and the need to consider multiple approaches when tackling mathematical problems. Exploring different arithmetic operations, considering sequences and series, and engaging in a deductive approach are all crucial problem-solving skills. The ambiguity highlights the need for a clear definition of the problem or the provision of additional clues. Further information regarding the origin or purpose of the sequence would greatly assist in finding a definitive answer. However, the process of exploration itself underscores the value of critical thinking and mathematical reasoning.
Latest Posts
Latest Posts
-
1 Gallon How Many Liter
Sep 23, 2025
-
1 3 As A Decimal Number
Sep 23, 2025
-
Long Division 2 Digit Divisor
Sep 23, 2025
-
650 Sq Feet In Meters
Sep 23, 2025
-
19 Celsius Converted To Fahrenheit
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6x 4x 6 24 9x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.