7/6 As A Mixed Number
saludintensiva
Sep 18, 2025 · 6 min read
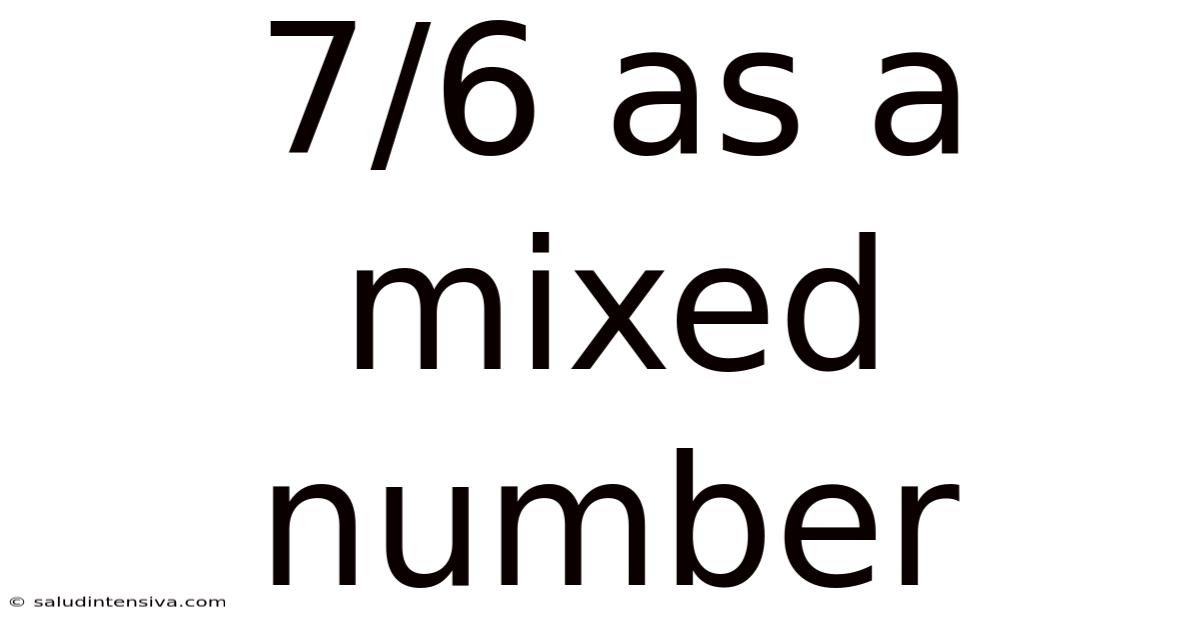
Table of Contents
Understanding 7/6 as a Mixed Number: A Comprehensive Guide
Fractions are a fundamental part of mathematics, representing parts of a whole. Sometimes, a fraction like 7/6, where the numerator (top number) is larger than the denominator (bottom number), is called an improper fraction. This guide will thoroughly explain how to convert an improper fraction like 7/6 into a mixed number, a number that combines a whole number and a proper fraction. We'll cover the process step-by-step, explore the underlying mathematical principles, answer frequently asked questions, and delve into practical applications. Understanding this concept is crucial for mastering arithmetic operations and building a strong foundation in mathematics.
What is a Mixed Number?
A mixed number represents a quantity that is greater than one. It's a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8). For instance, 1 1/2 (one and one-half) is a mixed number. It represents one whole unit plus half of another unit.
Converting 7/6 to a Mixed Number: A Step-by-Step Guide
Converting 7/6 to a mixed number involves dividing the numerator by the denominator. Here's the process:
-
Divide the numerator by the denominator: Divide 7 by 6. This gives us a quotient (the result of the division) and a remainder.
7 ÷ 6 = 1 with a remainder of 1
-
The quotient becomes the whole number part: The quotient, 1, becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction: The remainder, 1, becomes the numerator of the fraction part of our mixed number.
-
The denominator stays the same: The denominator of the original fraction, 6, remains the same in the fraction part of the mixed number.
-
Combine the whole number and the fraction: Putting it all together, we get the mixed number: 1 1/6
Therefore, 7/6 expressed as a mixed number is 1 1/6.
Visualizing the Conversion
Imagine you have seven identical slices of pizza. If each pizza is cut into six equal slices, you have more than one whole pizza. You have one whole pizza (6 slices) and one slice remaining out of the six slices that would make up a second pizza. This visually represents 1 1/6.
The Mathematical Principle Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the concept of division and the relationship between the numerator and the denominator. The improper fraction 7/6 essentially represents 7 divided by 6. Performing this division yields the whole number part and the remainder, which forms the fractional part of the mixed number. This process is a fundamental aspect of working with fractions and understanding their representation of quantities.
Working with Mixed Numbers: Addition and Subtraction
Once you understand how to convert improper fractions to mixed numbers, you can utilize this knowledge to perform addition and subtraction more efficiently. For example, adding 1 1/6 and 2 1/3 requires finding a common denominator, which simplifies if you first convert both mixed numbers into improper fractions and then back to a mixed number once the operation is complete.
- Converting back to an improper fraction: To convert 1 1/6 back to an improper fraction, multiply the whole number (1) by the denominator (6), add the numerator (1), and keep the same denominator (6). This results in (1*6 + 1)/6 = 7/6.
Similarly, to add 1 1/6 and 2 1/3:
- Convert to improper fractions: 7/6 + 7/3
- Find a common denominator: 7/6 + 14/6
- Add the numerators: 21/6
- Simplify: 3 3/6 = 3 1/2
Frequently Asked Questions (FAQ)
Q1: Why is it important to convert improper fractions to mixed numbers?
A1: Converting improper fractions to mixed numbers makes it easier to visualize and understand the quantity represented. Mixed numbers provide a more intuitive way to represent quantities larger than one. It also simplifies certain calculations, especially addition and subtraction of fractions.
Q2: Can all improper fractions be converted to mixed numbers?
A2: Yes, all improper fractions can be converted to mixed numbers. This is because the numerator is always greater than or equal to the denominator, meaning at least one whole unit is represented.
Q3: What if the remainder is zero after dividing the numerator by the denominator?
A3: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 6/3 = 2. In this case, there is no fractional part in the mixed number.
Q4: Are there any shortcuts for converting improper fractions to mixed numbers?
A4: While the long division method is straightforward and helps reinforce the underlying mathematical concept, some people find it faster to directly estimate the whole number part by considering how many times the denominator goes into the numerator. However, this method requires a strong grasp of multiplication and division facts and is prone to errors if not done carefully.
Q5: How do I convert a mixed number back to an improper fraction?
A5: To convert a mixed number (a b/c) to an improper fraction, follow these steps:
- Multiply the whole number (a) by the denominator (c): a * c
- Add the numerator (b): a * c + b
- Keep the same denominator (c): (a * c + b) / c
For example, to convert 1 1/6 back to an improper fraction: (1 * 6) + 1 = 7, so the improper fraction is 7/6.
Real-World Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and various fields:
-
Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities (e.g., 1 1/2 cups of flour).
-
Measurements: Measurements in carpentry, construction, and engineering often involve mixed numbers (e.g., 2 3/4 inches).
-
Time: We commonly use mixed numbers to express time (e.g., 1 1/2 hours).
-
Data Analysis: Mixed numbers can appear in data analysis reports and statistical presentations.
Conclusion
Understanding how to convert improper fractions to mixed numbers is a crucial skill in mathematics. This process involves dividing the numerator by the denominator, using the quotient as the whole number part, and the remainder as the numerator of the fractional part. The ability to convert between improper fractions and mixed numbers simplifies various mathematical operations and is essential for practical applications in numerous fields. Mastering this fundamental concept will undoubtedly improve your mathematical proficiency and problem-solving abilities. Through practice and application, you will develop a strong understanding of fractions and their representation of quantities. Remember to practice regularly to build confidence and fluency.
Latest Posts
Latest Posts
-
4 6 As A Decimal
Sep 18, 2025
-
3 8 Minus 1 4
Sep 18, 2025
-
2 3 4 To Improper Fraction
Sep 18, 2025
-
18 Percent In Decimal Form
Sep 18, 2025
-
Gcf Of 5 And 8
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 7/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.