7 Divided By 1 4
saludintensiva
Sep 12, 2025 · 5 min read
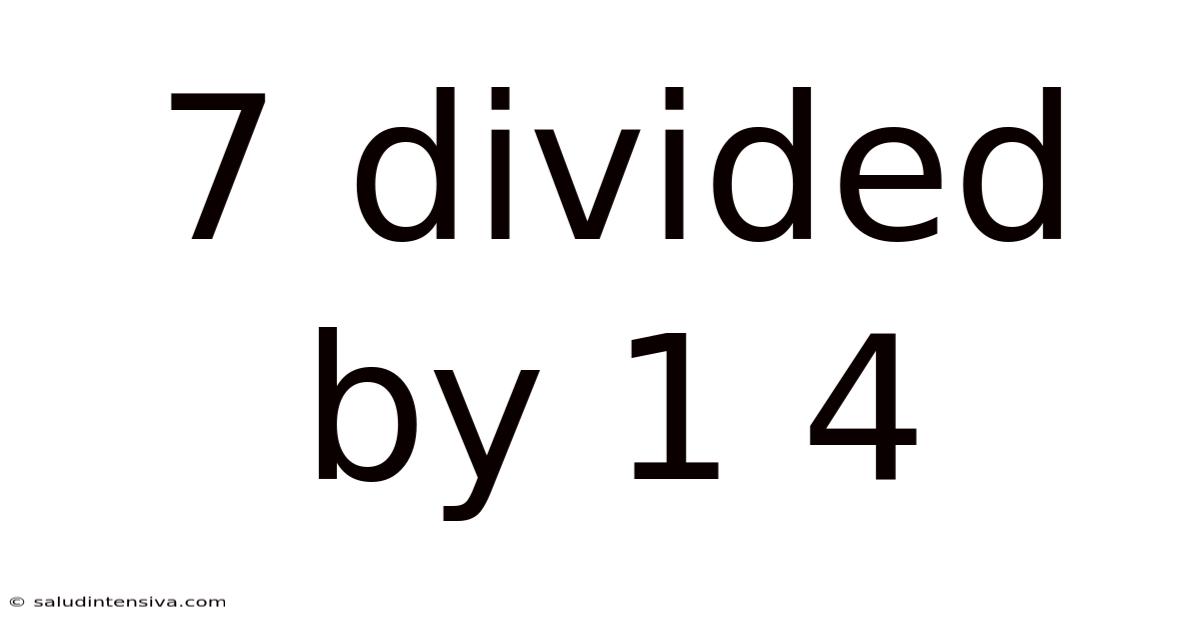
Table of Contents
Decoding 7 Divided by 1¼: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, especially when dealing with mixed numbers like 1¼. This comprehensive guide will break down the process of solving 7 divided by 1¼ step-by-step, explaining the underlying mathematical principles and providing practical applications. We'll explore different methods, address common misconceptions, and answer frequently asked questions, ensuring you gain a firm grasp of this essential mathematical concept. This guide is perfect for students struggling with fraction division, teachers looking for supplementary materials, or anyone wanting to refresh their understanding of elementary arithmetic.
Understanding the Problem: 7 ÷ 1¼
The problem, 7 ÷ 1¼, asks: "How many times does 1¼ fit into 7?" This seemingly simple question highlights the core concept of division: partitioning a whole into equal parts. Before diving into the solution, let's review some fundamental concepts.
Key Concepts: Fractions, Mixed Numbers, and Division
-
Fractions: A fraction represents a part of a whole. It's expressed as a/b, where 'a' is the numerator (the part) and 'b' is the denominator (the whole). For example, ½ represents one-half of a whole.
-
Mixed Numbers: A mixed number combines a whole number and a fraction, such as 1¼ (one and one-quarter). It represents a quantity greater than one.
-
Division: Division is the process of splitting a quantity into equal groups or parts. It's the inverse operation of multiplication.
Method 1: Converting to Improper Fractions
This is often the most efficient method for dividing fractions. The process involves converting both the whole number and the mixed number into improper fractions.
Step 1: Convert the mixed number to an improper fraction.
To convert 1¼ to an improper fraction, we multiply the whole number (1) by the denominator (4) and add the numerator (1). This sum (1*4 + 1 = 5) becomes the new numerator, while the denominator remains the same (4). Therefore, 1¼ becomes ⁵⁄₄.
Step 2: Convert the whole number to an improper fraction.
Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 7 can be written as ⁷⁄₁.
Step 3: Invert the divisor and multiply.
Dividing by a fraction is the same as multiplying by its reciprocal (the fraction flipped upside down). The reciprocal of ⁵⁄₄ is ⁴⁄₅. So, our problem becomes:
⁷⁄₁ × ⁴⁄₅
Step 4: Multiply the numerators and the denominators.
(7 × 4) / (1 × 5) = 28/5
Step 5: Simplify the result (if necessary).
The improper fraction 28/5 can be converted back into a mixed number. We divide the numerator (28) by the denominator (5): 28 ÷ 5 = 5 with a remainder of 3. This means 28/5 is equal to 5⅗.
Therefore, 7 ÷ 1¼ = 5⅗
Method 2: Using Long Division
While less common for fraction division, long division can be applied after converting the mixed number to a decimal.
Step 1: Convert the mixed number to a decimal.
1¼ is equal to 1.25 (because ¼ is 0.25).
Step 2: Perform long division.
Divide 7 by 1.25 using long division:
5.6
1.25 | 7.00
-6.25
-----
0.750
-0.750
-----
0
Therefore, 7 ÷ 1.25 = 5.6
Step 3: Convert the decimal to a fraction (if necessary).
5.6 can be expressed as ⁵⁶⁄₁₀ which simplifies to ¹⁴⁄₅. This is the same as 5⅗.
Method 3: Repeated Subtraction
This method is conceptually simpler, though less efficient for larger numbers. It visually demonstrates what division represents.
We repeatedly subtract 1¼ from 7 until we reach zero or a value less than 1¼. Each subtraction represents one "group" of 1¼.
- 7 - 1¼ = 5¾
- 5¾ - 1¼ = 4½
- 4½ - 1¼ = 3¼
- 3¼ - 1¼ = 2
- 2 - 1¼ = ¾
We subtracted 1¼ five times. The remaining ¾ represents a fraction of the group. Thus, we have 5 full groups of 1¼ and ¾ of another group, which again gives us 5⅗.
Practical Applications
Understanding fraction division is crucial in various real-world scenarios:
-
Cooking: Dividing ingredients for multiple servings. If a recipe calls for 1¼ cups of flour for one cake, and you want to make 7 cakes, you'll need to calculate 7 ÷ 1¼ cups of flour.
-
Construction: Calculating the number of materials needed for a project. For example, if each section of a fence requires 1¼ meters of wood, and you need a total of 7 meters, you can determine the number of sections using division.
-
Sewing: Cutting fabric into equal pieces. If you have 7 meters of fabric and need to cut pieces of 1¼ meters each, this division will help determine how many pieces you can make.
Frequently Asked Questions (FAQ)
-
Q: Why do we invert the divisor and multiply when dividing fractions?
-
A: Dividing by a fraction is essentially asking "how many times does this fraction fit into the whole?" Inverting and multiplying efficiently addresses this question. Consider the example of dividing by ½. This means asking, "how many halves are in the whole?" There are two halves in one whole, which aligns with the reciprocal method: 1 ÷ ½ = 1 × 2/1 = 2.
-
Q: Can I use a calculator to solve this problem?
-
A: Yes, most calculators can handle fraction division. However, understanding the underlying mathematical principles is crucial for solving similar problems without a calculator.
-
Q: Which method is best?
-
A: The method of converting to improper fractions is generally the most efficient and widely applicable method for dividing fractions and mixed numbers. However, understanding the concept through methods like repeated subtraction can enhance comprehension.
-
Q: What if the result is a decimal?
-
A: A decimal result is perfectly acceptable. You can convert it back to a fraction if needed, depending on the context of the problem.
Conclusion
Dividing 7 by 1¼ yields 5⅗ or 5.6. This guide has explored three different methods for solving this problem, emphasizing the importance of converting mixed numbers to improper fractions for efficient calculation. We have also touched upon practical applications and answered frequently asked questions, hoping to provide a solid foundation for understanding and applying fraction division in various contexts. Remember, the key to mastering fraction division lies in understanding the underlying concepts and choosing the method that works best for you. Practice is key to solidifying this important mathematical skill. Don't hesitate to work through similar problems to reinforce your understanding.
Latest Posts
Latest Posts
-
14 3 As A Mixed Number
Sep 12, 2025
-
29 Acres To Square Feet
Sep 12, 2025
-
What Time Is 15 35
Sep 12, 2025
-
Gcf Of 12 And 3
Sep 12, 2025
-
What Is Equivalent To 612
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 7 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.