7 Out Of 20 Percentage
saludintensiva
Sep 14, 2025 · 5 min read
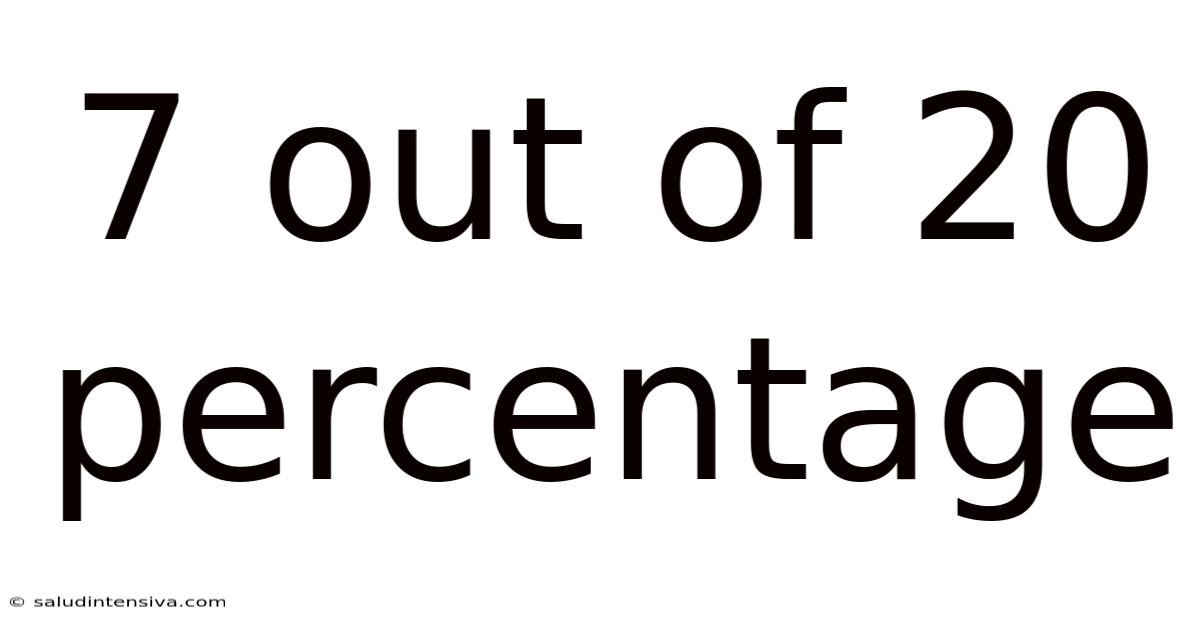
Table of Contents
Understanding 7 out of 20: A Comprehensive Guide to Percentages, Fractions, and Decimals
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to express a part of a whole as a percentage is crucial. This article dives deep into understanding what 7 out of 20 represents, exploring its fractional, decimal, and percentage equivalents, and demonstrating its practical application through various examples. We'll also address common misconceptions and answer frequently asked questions to build a robust understanding of this seemingly simple yet versatile concept.
Understanding the Basics: Fractions, Decimals, and Percentages
Before we delve into the specifics of 7 out of 20, let's establish a solid foundation in the relationship between fractions, decimals, and percentages.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For example, 1/2 (one-half) means one part out of two equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with a decimal point separating the whole number from the fractional part. For example, 0.5 is equivalent to 1/2.
-
Percentages: A percentage represents a fraction or decimal expressed as parts per hundred. The symbol "%" indicates "percent" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Expressing 7 out of 20 in Different Forms
Now, let's focus on "7 out of 20." This phrase inherently represents a fraction, where 7 is the part and 20 is the whole.
-
Fraction: The simplest representation is the fraction 7/20. This fraction is already in its simplest form, as 7 and 20 share no common factors other than 1.
-
Decimal: To convert the fraction 7/20 to a decimal, we divide the numerator (7) by the denominator (20): 7 ÷ 20 = 0.35.
-
Percentage: To express 7/20 as a percentage, we multiply the decimal equivalent (0.35) by 100: 0.35 × 100 = 35%. Therefore, 7 out of 20 is equivalent to 35%.
Practical Applications and Real-World Examples
Understanding 7 out of 20, or 35%, has numerous practical applications in various scenarios:
-
Test Scores: Imagine a student taking a 20-question test and answering 7 questions correctly. Their score would be 7/20, or 35%.
-
Sales and Discounts: A store offering a 35% discount on an item means that the customer pays only 65% (100% - 35%) of the original price.
-
Surveys and Statistics: If a survey of 20 people reveals that 7 prefer a particular product, then 35% of the respondents prefer that product. This percentage can be used to analyze consumer preferences and guide business decisions.
-
Probability: In a scenario with 20 equally likely outcomes, the probability of a specific event occurring 7 times would be 7/20, or 35%.
-
Financial Calculations: Many financial calculations involve percentages. Understanding 35% is essential for calculating interest, returns on investments, tax rates, and more. For example, a 35% interest rate on a loan would mean you pay 35% of the principal amount as interest.
Expanding the Understanding: Working with Percentages
Let's explore some common percentage calculations involving the 35% derived from 7 out of 20:
-
Finding a Percentage of a Number: To find 35% of a number, multiply the number by 0.35 (the decimal equivalent of 35%). For example, 35% of 100 is 100 * 0.35 = 35. 35% of 50 is 50 * 0.35 = 17.5.
-
Finding the Original Number from a Percentage: If you know a percentage of a number and the percentage itself, you can find the original number. For example, if 35% of a number is 7, then the original number is 7 / 0.35 = 20.
-
Calculating Percentage Increase or Decrease: To calculate a percentage increase or decrease, find the difference between the original and new value, divide the difference by the original value, and multiply by 100. For example, if a value increases from 20 to 27, the percentage increase is ((27-20)/20) * 100 = 35%.
Advanced Concepts and Related Topics
While understanding 7 out of 20 is relatively straightforward, it opens doors to more advanced concepts:
-
Proportions: The concept of 7 out of 20 is inherently a proportion. Proportions are mathematical statements that show two ratios are equal. Understanding proportions is essential for solving problems involving scaling, ratios, and rates.
-
Statistical Analysis: Percentages are fundamental in statistical analysis. They are used to represent frequencies, probabilities, and other important metrics in data analysis and interpretation.
-
Financial Modeling: In finance, percentage calculations are extensively used to create financial models that forecast future performance, assess risk, and make informed investment decisions.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of the fraction 7/20?
- A: 7/20 is already in its simplest form because 7 and 20 share no common factors other than 1.
-
Q: How do I convert 7/20 to a decimal?
- A: Divide the numerator (7) by the denominator (20): 7 ÷ 20 = 0.35.
-
Q: How do I convert 7/20 to a percentage?
- A: Multiply the decimal equivalent (0.35) by 100: 0.35 × 100 = 35%.
-
Q: What if I have a different fraction, say 11/25? How would I convert it to a percentage?
- A: First, convert the fraction to a decimal by dividing the numerator (11) by the denominator (25): 11 ÷ 25 = 0.44. Then, multiply the decimal by 100 to get the percentage: 0.44 × 100 = 44%.
-
Q: Are there any online calculators that can help with percentage calculations?
- A: While this article focuses on the conceptual understanding, numerous online calculators are available to perform percentage calculations quickly and efficiently.
Conclusion
Understanding the concept of 7 out of 20, its fractional, decimal, and percentage equivalents, and its applications extends far beyond a simple mathematical calculation. It's a fundamental building block for understanding more complex mathematical concepts and solving real-world problems across diverse fields. By mastering the conversion between fractions, decimals, and percentages, you equip yourself with a vital tool for interpreting data, making informed decisions, and effectively communicating quantitative information. The seemingly simple concept of 7 out of 20, or 35%, is a powerful foundation for numerical literacy and analytical thinking. Remember to practice these concepts regularly to solidify your understanding and build confidence in your ability to work with percentages effectively.
Latest Posts
Latest Posts
-
3 50 As A Decimal
Sep 14, 2025
-
What Is 7 Degrees C
Sep 14, 2025
-
Surface Area Formula Calc 2
Sep 14, 2025
-
1 Out Of 3 Percentage
Sep 14, 2025
-
Variance Of A Dice Roll
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 20 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.