70 Percent As A Decimal
saludintensiva
Sep 23, 2025 · 5 min read
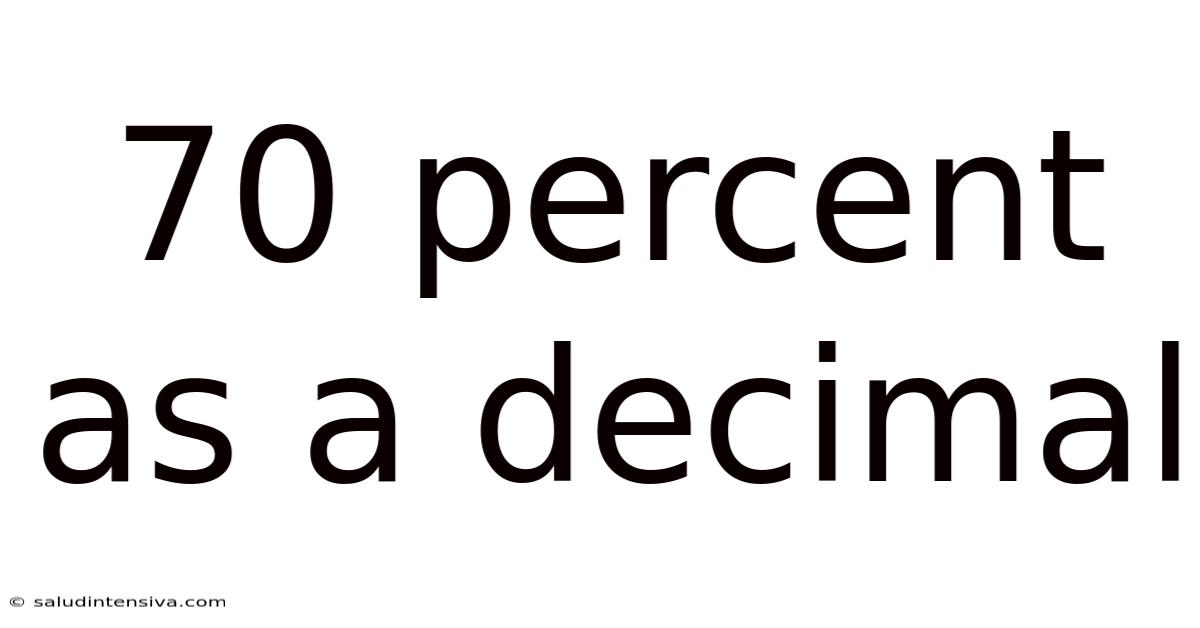
Table of Contents
70 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts and taxes to comprehending financial reports and statistical data. This comprehensive guide will delve into the conversion of 70 percent to its decimal form, exploring the underlying principles and providing practical examples to solidify your understanding. We'll move beyond the simple conversion and explore how this knowledge applies to broader mathematical concepts and real-world scenarios.
Understanding Percentages and Decimals
Before we directly address converting 70 percent to a decimal, let's establish a strong foundation by understanding the core concepts of percentages and decimals.
A percentage represents a fraction of 100. The word "percent" literally means "per hundred" ( per centum in Latin). So, 70% signifies 70 parts out of 100. This can be expressed as a fraction (70/100) or as a decimal.
A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. Decimals are a convenient way to represent fractions, particularly when dealing with calculations.
Converting 70 Percent to a Decimal: The Simple Method
The most straightforward way to convert 70% to a decimal is to divide the percentage by 100. This is because a percentage is fundamentally a fraction with a denominator of 100.
Therefore:
70% = 70/100
Dividing 70 by 100 gives us:
70/100 = 0.7
Therefore, 70 percent as a decimal is 0.7.
Understanding the Process: A Deeper Dive
The conversion from percentage to decimal involves understanding the positional value of digits in the decimal system. When we divide by 100, we essentially move the decimal point two places to the left. Every whole number has an implied decimal point at the end (e.g., 70 is the same as 70.0). Moving the decimal point two places to the left effectively divides the number by 100.
Let's illustrate this with another example: Converting 25% to a decimal.
25% = 25/100 = 0.25
Notice how the decimal point in 25.0 moves two places to the left to become 0.25.
Converting Decimals to Percentages: The Reverse Process
It's equally important to understand the reverse process – converting a decimal to a percentage. This involves multiplying the decimal by 100 and adding the "%" symbol.
For example, to convert 0.7 back to a percentage:
0.7 x 100 = 70
Adding the percentage symbol gives us 70%.
Practical Applications of 70% as a Decimal (0.7)
The decimal equivalent of 70% (0.7) has numerous applications in various fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates frequently involves using decimal representations of percentages. For example, a 70% discount on a $100 item would be calculated as 0.7 * $100 = $70.
-
Statistics: Probabilities, proportions, and statistical analyses often involve decimal representations. A 70% probability of an event occurring is represented as 0.7.
-
Science: Many scientific calculations and measurements rely on decimal representations of percentages, such as expressing concentrations of solutions or experimental results.
-
Everyday Life: Calculating tips, sales tax, or determining the portion of a bill you need to pay often involves using decimals derived from percentages.
Advanced Applications and Related Concepts
Beyond the basic conversion, understanding 70% as a decimal (0.7) opens doors to more advanced mathematical concepts:
-
Fractions: 0.7 is also equivalent to the fraction 7/10. Understanding the relationship between decimals, percentages, and fractions is crucial for solving various mathematical problems.
-
Proportions: Solving proportions often involves converting percentages to decimals to simplify calculations. For example, if 70% of x is 140, we can set up the equation 0.7x = 140 and solve for x.
-
Algebra: Decimals are frequently used in algebraic equations and expressions. Understanding decimal representation of percentages is essential for solving these equations.
-
Calculus: Derivatives and integrals often involve working with decimal representations of numbers, including those derived from percentages.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to convert percentages to decimals?
A: Yes, most calculators have a percentage function that can directly convert percentages to decimals. Alternatively, you can simply divide the percentage by 100.
Q: Why is it important to understand the decimal equivalent of percentages?
A: Understanding decimal equivalents allows for easier calculations, particularly when using calculators or computers. Decimals are also essential for many mathematical and scientific applications.
Q: Are there any other ways to convert 70% to a decimal besides dividing by 100?
A: While dividing by 100 is the most direct and common method, you could also think of it as multiplying by 0.01 (since 1/100 = 0.01). The result would be the same: 70 x 0.01 = 0.7.
Q: What if I have a percentage with a decimal, like 70.5%?
A: The process remains the same: divide by 100. 70.5% = 70.5/100 = 0.705.
Q: How do I convert a decimal to a percentage with more than two decimal places?
A: Multiply the decimal by 100 and add the "%" symbol. For example, 0.705 x 100 = 70.5%, and 0.1234 x 100 = 12.34%.
Conclusion
Converting 70 percent to its decimal equivalent, 0.7, is a simple yet crucial skill. This seemingly basic conversion underpins numerous applications in various fields, from everyday financial calculations to complex scientific analyses. Understanding the principles behind this conversion, and the broader connections to fractions, proportions, and other mathematical concepts, solidifies a fundamental understanding of numerical representation and empowers you to confidently tackle a wide range of mathematical problems. Remember that mastery comes from practice. Try converting different percentages to decimals and vice versa to reinforce your understanding and build your skills.
Latest Posts
Latest Posts
-
Inch Pound To Foot Pounds
Sep 23, 2025
-
Ppi To Dpi Conversion Calculator
Sep 23, 2025
-
4 2 3 As Decimal
Sep 23, 2025
-
48 Inches Tall In Feet
Sep 23, 2025
-
How Many Gallons Gas Tank
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 70 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.