8 125 In Decimal Form
saludintensiva
Sep 12, 2025 · 5 min read
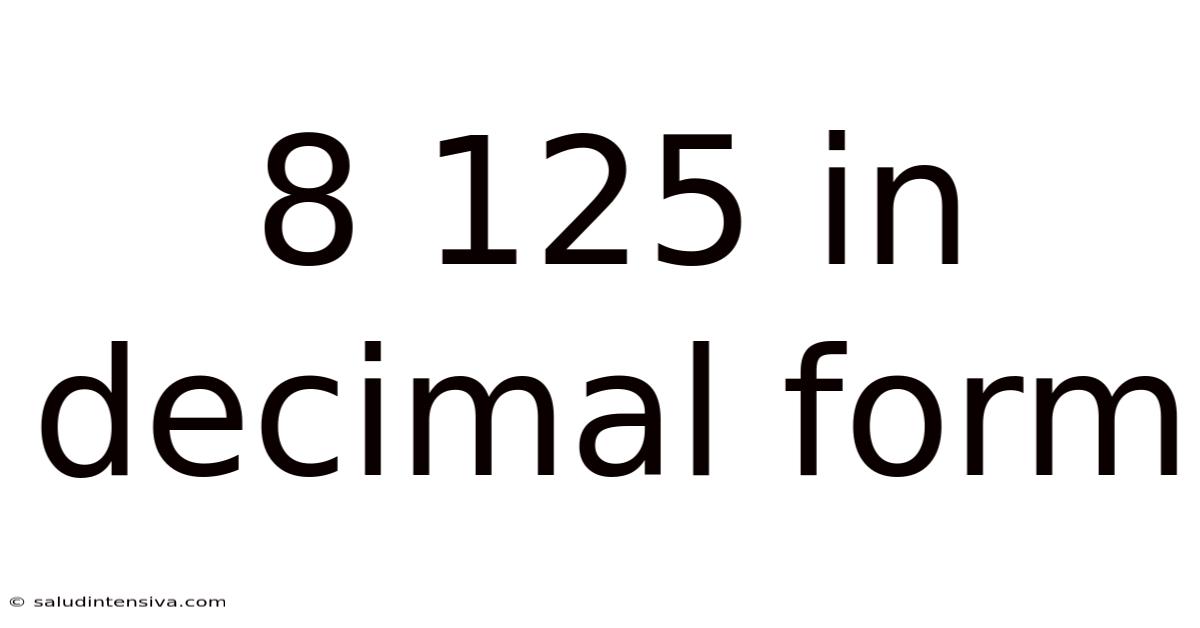
Table of Contents
Unveiling the Mystery: 8 125 in Decimal Form and Beyond
Understanding different number systems is crucial in mathematics and computer science. This article delves deep into the seemingly simple question: what is 8 125 in decimal form? While the answer might seem immediately obvious to those familiar with base-10 systems, we'll explore the underlying principles, discuss potential ambiguities, and expand our understanding to include other number systems, highlighting the importance of context and clarity in mathematical representation. We will also address common misconceptions and frequently asked questions.
Understanding Decimal Numbers (Base-10)
Before tackling 8 125, let's solidify our understanding of the decimal system. The decimal system, also known as the base-10 system, is the most commonly used number system worldwide. It uses ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) to represent all numbers. The position of each digit determines its value. Moving from right to left, each digit represents a progressively higher power of 10.
For example, the number 1234 can be broken down as follows:
- 4 × 10⁰ (4 ones)
- 3 × 10¹ (3 tens)
- 2 × 10² (2 hundreds)
- 1 × 10³ (1 thousand)
Therefore, 1234 is simply the sum: 4 + 30 + 200 + 1000 = 1234.
Interpreting "8 125": Addressing Potential Ambiguities
The number "8 125" presents a slight ambiguity. The presence of a space suggests a potential separation, implying perhaps a grouping or a different number system entirely. Without further context, we can consider two likely interpretations:
-
8,125 (as a single decimal number): This is the most straightforward interpretation. The space acts as a thousands separator, making the number easily readable. In this case, 8 125 in decimal form is simply 8,125.
-
Two separate numbers: 8 and 125: This interpretation is less likely unless explicitly stated, but it's crucial to acknowledge the possibility. In this case, we have two distinct decimal numbers, 8 and 125.
For the remainder of this article, we'll primarily focus on the first and most likely interpretation: 8,125 as a single decimal number.
Expanding the Concept: Other Number Systems
While the decimal system is prevalent, other number systems exist. Understanding these systems helps appreciate the fundamental principles of representing numbers. Let's briefly explore two important alternatives:
-
Binary (Base-2): The binary system is crucial in computer science. It uses only two digits: 0 and 1. Each position represents a power of 2. Converting decimal 8,125 to binary would involve repeated division by 2, recording the remainders. The result is a much longer string of 0s and 1s.
-
Hexadecimal (Base-16): The hexadecimal system uses 16 digits (0-9 and A-F, where A=10, B=11, C=12, D=13, E=14, F=15). This system is often used in computer programming and data representation because it offers a more compact way to represent binary data. Converting 8,125 to hexadecimal would again involve a series of divisions, this time by 16.
The conversion process between decimal and other number systems involves algorithms that are beyond the scope of this article, but readily available online and in mathematical textbooks.
Practical Applications of Understanding Number Systems
The ability to work with different number systems isn't merely a theoretical exercise. It has practical applications in various fields:
-
Computer Science: As mentioned before, binary and hexadecimal are fundamental to how computers process and store information. Understanding these systems is essential for programmers, software developers, and anyone working with computer hardware.
-
Cryptography: Cryptographic systems often rely on number theory and operations in different number systems (including very large numbers and prime numbers) for encryption and decryption processes.
-
Data Analysis: Understanding various number systems can be crucial for interpreting data represented in different formats or from various sources.
-
Telecommunications: Signal encoding and transmission in telecommunications systems often involve the manipulation of binary or other non-decimal number systems.
Frequently Asked Questions (FAQ)
Q1: Is there a difference between 8125 and 8,125?
A1: In the context of the decimal system, the comma (or a period in some locales) is typically used as a thousands separator to improve readability. It does not alter the numerical value. Therefore, 8125 and 8,125 represent the same number.
Q2: How do I convert 8,125 to other number systems (like binary or hexadecimal)?
A2: Conversion to binary or hexadecimal involves repeated division by the base of the target system (2 for binary, 16 for hexadecimal). The remainders are then collected and written in reverse order to obtain the equivalent representation in the new base. Online calculators and software readily perform these conversions.
Q3: Why are other number systems important?
A3: Different number systems have varying strengths and weaknesses. Binary is ideal for digital computers due to its simplicity (only two states, 0 and 1), while hexadecimal provides a compact representation of binary data. The decimal system is more intuitive for human use in everyday calculations.
Q4: Can 8,125 be expressed in Roman numerals?
A4: Yes, while cumbersome, 8,125 can be represented in Roman numerals. It would be written as VIII MCLXXV. (VIII = 8000, M = 1000, CL = 150, XXV = 25)
Conclusion: Beyond the Simple Answer
While the immediate answer to "8 125 in decimal form" is straightforward – 8,125 – this question serves as a springboard to explore the broader world of number systems. Understanding the underlying principles of different number systems, their interrelationships, and their practical applications is crucial for anyone seeking a deeper understanding of mathematics and its applications in various fields. From computer programming to cryptography, the ability to work with different numerical bases is a valuable asset, highlighting the importance of a foundational grasp of mathematical concepts and their real-world relevance. The seemingly simple number 8,125 becomes a gateway to a wealth of knowledge and understanding when viewed within the wider context of numerical representation.
Latest Posts
Latest Posts
-
0 25 Acre To Sq Ft
Sep 12, 2025
-
Is 247 A Prime Number
Sep 12, 2025
-
Gcf Of 50 And 80
Sep 12, 2025
-
How To Find Standard Notation
Sep 12, 2025
-
7 10 Is What Percent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 8 125 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.