8 2/3 As A Decimal
saludintensiva
Sep 16, 2025 · 5 min read
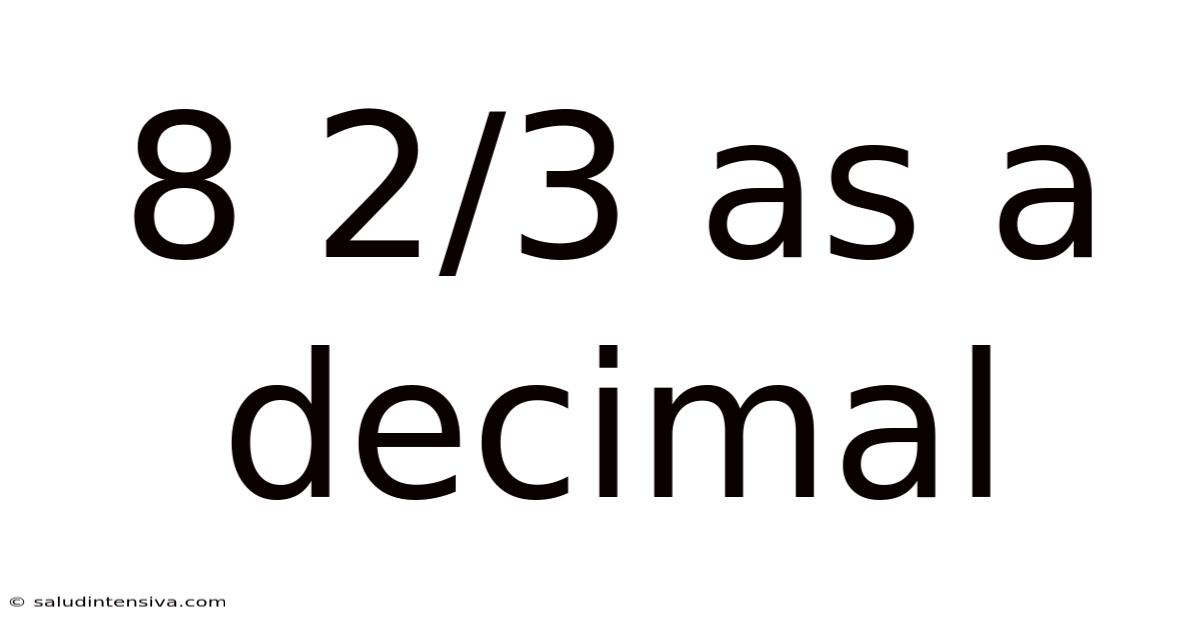
Table of Contents
Understanding 8 2/3 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 8 2/3 into its decimal equivalent, exploring the underlying principles and offering practical examples to solidify your understanding. We'll cover multiple methods, address common misconceptions, and provide answers to frequently asked questions. This article will equip you with a clear and concise understanding of how to tackle this and similar conversions.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's briefly review the concepts of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 8 2/3. This represents 8 whole units plus 2/3 of another unit. A fraction, in its simplest form, represents a part of a whole. The numerator (top number) indicates the number of parts we have, while the denominator (bottom number) indicates the total number of equal parts the whole is divided into.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward approach. We'll first convert the fractional part (2/3) into a decimal and then add the whole number (8).
Step 1: Divide the numerator by the denominator.
To convert 2/3 to a decimal, we perform the division: 2 ÷ 3. This results in a repeating decimal: 0.66666... This is often represented as 0.6̅, where the bar indicates the digit or digits that repeat infinitely.
Step 2: Add the whole number.
Now, add the whole number part: 8 + 0.66666... = 8.66666...
Therefore, 8 2/3 as a decimal is approximately 8.6667 (rounded to four decimal places). It's important to note that this is an approximation, as the decimal representation of 2/3 is an infinitely repeating decimal.
Method 2: Converting the Entire Mixed Number into an Improper Fraction
Another method involves first converting the mixed number into an improper fraction, and then dividing the numerator by the denominator.
Step 1: Convert to an improper fraction.
To convert 8 2/3 to an improper fraction, we multiply the whole number (8) by the denominator (3), add the numerator (2), and keep the same denominator (3). This gives us:
(8 × 3) + 2 = 26
So, 8 2/3 becomes 26/3.
Step 2: Divide the numerator by the denominator.
Now, divide the numerator (26) by the denominator (3): 26 ÷ 3 = 8.66666...
Again, we arrive at the same approximate decimal value: 8.6667 (rounded to four decimal places).
Method 3: Using a Calculator
Modern calculators can easily handle this conversion. Simply enter "8 + 2/3" or "26/3" into your calculator, and it will provide the decimal equivalent, likely displaying 8.666666... or a rounded version. While this method is convenient, understanding the underlying mathematical processes is crucial for developing a strong foundational understanding of numbers and their representations.
Understanding Repeating Decimals
The decimal representation of 8 2/3 highlights the concept of repeating decimals. These are decimals where one or more digits repeat infinitely. In this case, the digit 6 repeats endlessly. Understanding repeating decimals is vital for accurate calculations and avoiding rounding errors. While we often round repeating decimals for practical purposes, it's important to acknowledge their infinite nature.
Significance and Applications
The conversion of fractions to decimals holds significant practical value across various fields:
- Finance: Calculating percentages, interest rates, and profit margins often require converting fractions to decimals.
- Engineering and Science: Precise measurements and calculations frequently involve decimal representations.
- Computer Science: Decimal representation is fundamental in many programming applications.
- Everyday Life: Dividing quantities, calculating proportions, and understanding unit conversions necessitate a strong understanding of fractions and decimals.
Common Mistakes to Avoid
- Incorrectly converting to an improper fraction: Ensure you correctly multiply the whole number by the denominator and add the numerator before placing it over the original denominator.
- Rounding prematurely: Avoid rounding off the decimal representation during intermediate steps of the calculation. Round only at the final stage, if necessary, to the required level of precision.
- Confusing numerator and denominator: Always remember the numerator is the top number and the denominator is the bottom number.
Frequently Asked Questions (FAQs)
Q1: Is 8.6667 the exact decimal representation of 8 2/3?
A1: No, 8.6667 is an approximation. The exact decimal representation is 8.6̅, indicating that the digit 6 repeats infinitely.
Q2: How can I represent 8 2/3 as a decimal without rounding?
A2: You can represent it as 8.6̅, using the bar notation to show the repeating digit.
Q3: What if I have a more complex mixed number, say 15 7/11? How would I convert it to a decimal?
A3: You would follow the same principles. First, convert 15 7/11 to an improper fraction: (15 x 11) + 7 = 172. Then divide 172 by 11: 172 ÷ 11 ≈ 15.636363... Again, this is a repeating decimal.
Q4: Are there any online tools or calculators that can help with these conversions?
A4: Many online calculators and math tools are available that can perform fraction to decimal conversions. However, it’s beneficial to understand the underlying mathematical process to ensure you can confidently perform the conversions yourself.
Conclusion
Converting 8 2/3 to a decimal, whether through direct division of the fraction, converting to an improper fraction first, or using a calculator, reinforces the fundamental relationship between fractions and decimals. Understanding the process, including the concept of repeating decimals and avoiding common pitfalls, is essential for building a solid foundation in mathematics. While calculators provide a convenient solution, grasping the underlying principles empowers you to solve similar problems with confidence and accuracy, across various mathematical and real-world applications. Remember, the key is not just to find the answer but to understand why the answer is what it is. This deeper understanding will serve you well in your future mathematical endeavors.
Latest Posts
Latest Posts
-
39 40 As A Decimal
Sep 16, 2025
-
3 To The 1 2 Power
Sep 16, 2025
-
17 24 As A Percentage
Sep 16, 2025
-
What Is 4 Of 85000
Sep 16, 2025
-
How To Calculate Percentage Excel
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 8 2/3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.