8.25 As A Mixed Number
saludintensiva
Sep 18, 2025 · 6 min read
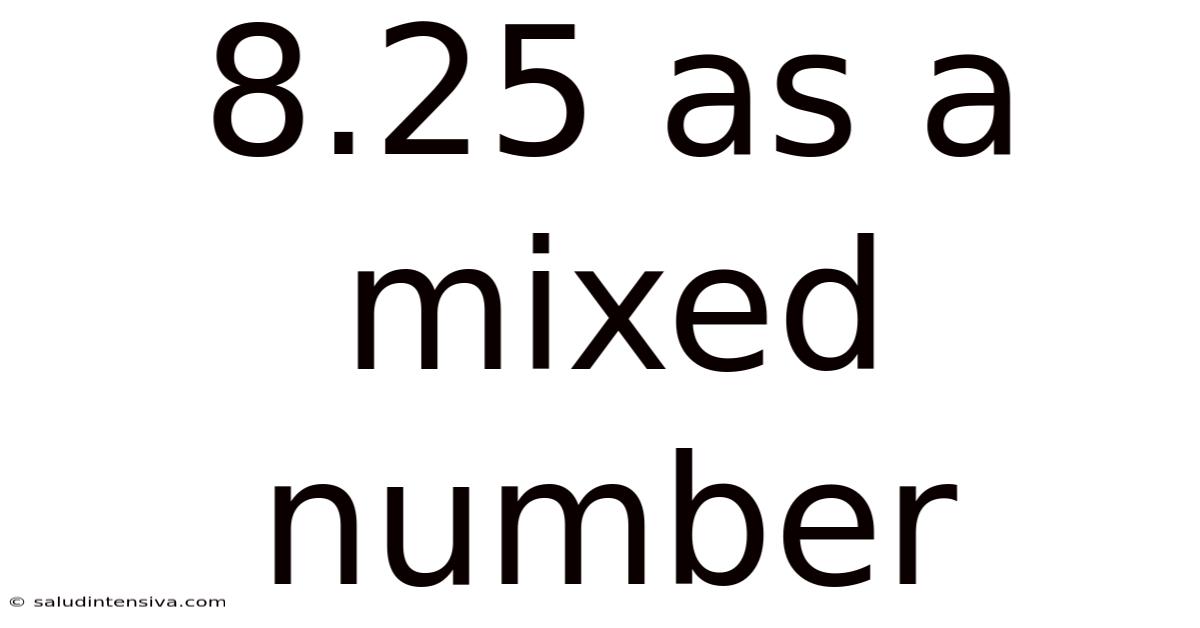
Table of Contents
Understanding 8.25 as a Mixed Number: A Comprehensive Guide
The seemingly simple decimal 8.25 holds a wealth of mathematical understanding, particularly when we explore its representation as a mixed number. This article will delve deep into the conversion process, providing not only the solution but also a thorough explanation of the underlying concepts. We will explore various methods, address common misconceptions, and even delve into the practical applications of understanding mixed numbers. By the end, you'll not only know that 8.25 is equivalent to 8 and 1/4, but you'll also grasp the fundamental principles involved in converting decimals to mixed numbers.
Understanding Decimals and Mixed Numbers
Before we jump into the conversion of 8.25, let's clarify the definitions of decimals and mixed numbers.
-
Decimals: Decimals are a way of representing numbers that are not whole numbers. They use a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.). For example, in 8.25, the '8' represents eight whole units, the '2' represents two tenths (2/10), and the '5' represents five hundredths (5/100).
-
Mixed Numbers: A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For instance, 3 ¼ is a mixed number, where '3' is the whole number part and '¼' is the fractional part. Mixed numbers are a useful way to represent quantities that are larger than one but not a whole number.
Converting 8.25 to a Mixed Number: Step-by-Step Guide
There are several ways to convert the decimal 8.25 into a mixed number. Let's explore two common methods:
Method 1: Understanding Place Value
This method directly utilizes the place value system inherent in decimals.
-
Identify the whole number part: The whole number part of 8.25 is simply 8. This will be the whole number component of our mixed number.
-
Convert the decimal part to a fraction: The decimal part is 0.25. This represents 25 hundredths, which can be written as the fraction 25/100.
-
Simplify the fraction: The fraction 25/100 can be simplified by finding the greatest common divisor (GCD) of 25 and 100. The GCD is 25. Dividing both the numerator and denominator by 25 gives us 1/4.
-
Combine the whole number and the simplified fraction: Combining the whole number part (8) and the simplified fraction (1/4), we get the mixed number 8 ¼.
Method 2: Using the Power of Ten
This method leverages the fact that decimals are based on powers of 10.
-
Rewrite the decimal as a fraction: The decimal 8.25 can be written as the fraction 825/100. This represents 825 hundredths.
-
Simplify the fraction (if possible): Similar to Method 1, we simplify 825/100 by finding the GCD of 825 and 100. The GCD is 25. Dividing both the numerator and the denominator by 25 gives us 33/4.
-
Convert the improper fraction to a mixed number: Since the numerator (33) is greater than the denominator (4), we have an improper fraction. To convert it to a mixed number, we perform division: 33 ÷ 4 = 8 with a remainder of 1. This means 33/4 is equivalent to 8 and 1/4.
Why are Mixed Numbers Important?
Understanding how to convert decimals to mixed numbers is crucial for several reasons:
-
Real-world applications: Many everyday situations require the use of mixed numbers. Imagine measuring ingredients for a recipe or calculating distances. While decimals are used in some contexts, mixed numbers are often more intuitive and easier to work with in practical scenarios.
-
Fractional arithmetic: Mixed numbers are essential for performing addition, subtraction, multiplication, and division involving fractions. Converting decimals to mixed numbers simplifies these calculations, especially when dealing with fractions with common denominators.
-
Enhanced understanding of fractions: The conversion process reinforces the relationship between decimals and fractions, deepening your understanding of these fundamental mathematical concepts.
-
Precision and Accuracy: In some fields, like engineering or construction, using mixed numbers provides a level of precision that a simple decimal might lack. A measurement of 8 1/4 inches is much clearer than 8.25 inches in terms of practical application.
Addressing Common Misconceptions
A common mistake is incorrectly converting the decimal part directly into a mixed number without considering the whole number component. Remember, 0.25 alone is 1/4, not 8 1/4. The whole number part (8) must be retained throughout the conversion process.
Another potential pitfall is failing to simplify the fraction. While 25/100 is correct, simplifying it to 1/4 is essential for presenting the mixed number in its simplest form. This not only makes it easier to work with but also ensures clarity and consistency in mathematical calculations.
Beyond the Basics: Exploring Further Applications
The conversion of decimals to mixed numbers forms the basis for many more complex mathematical operations. It’s crucial for understanding topics such as:
-
Percentage Calculations: Understanding mixed numbers is often beneficial when calculating percentages, particularly when dealing with fractions of percentages.
-
Ratio and Proportion Problems: Mixed numbers can often simplify the representation and manipulation of ratios and proportions, making problem-solving more efficient.
-
Geometry and Measurement: In fields involving precise measurements, using mixed numbers can avoid confusion and ensure accuracy.
-
Algebraic Equations: Mixed numbers can appear in algebraic equations, and understanding their conversion to improper fractions is vital for solving these equations.
Frequently Asked Questions (FAQ)
-
Q: Can every decimal be converted into a mixed number?
- A: No, only decimals that represent numbers greater than 1 can be converted to a mixed number. Decimals less than 1 are represented by proper fractions.
-
Q: What if the decimal has more digits after the decimal point?
- A: The same principle applies. For example, to convert 12.375, you would first identify the whole number (12), then convert 0.375 to a fraction (375/1000), simplify it (3/8), and finally combine it with the whole number to get 12 3/8.
-
Q: Is there a quicker method for converting simple decimals?
- A: For simple decimals like 0.25, 0.5, and 0.75, many people memorize their fractional equivalents (1/4, 1/2, and 3/4 respectively). This speeds up the conversion process.
-
Q: Why do we need both decimals and mixed numbers?
- A: Decimals are excellent for calculations using calculators or computers. Mixed numbers, however, offer a more intuitive and practical representation, especially in everyday scenarios and when dealing with fractions.
Conclusion
Converting 8.25 to a mixed number, resulting in 8 ¼, is more than just a simple mathematical operation. It's a fundamental step in understanding the interconnectedness of decimals and fractions. This understanding lays the groundwork for tackling more complex mathematical problems and applying these concepts to real-world situations. Mastering this conversion not only enhances your mathematical skills but also helps you develop a deeper appreciation for the versatility and power of numerical representation. By grasping the underlying principles and practicing different methods, you can confidently navigate the world of decimals and mixed numbers with increased proficiency and understanding.
Latest Posts
Latest Posts
-
Ones Tens Hundreds Thousands Chart
Sep 18, 2025
-
1 3 To The Second Power
Sep 18, 2025
-
7 4 As A Fraction
Sep 18, 2025
-
3 4 Plus 1 4
Sep 18, 2025
-
32 Deg C To Fahrenheit
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 8.25 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.