8 7/8 As A Decimal
saludintensiva
Sep 16, 2025 · 5 min read
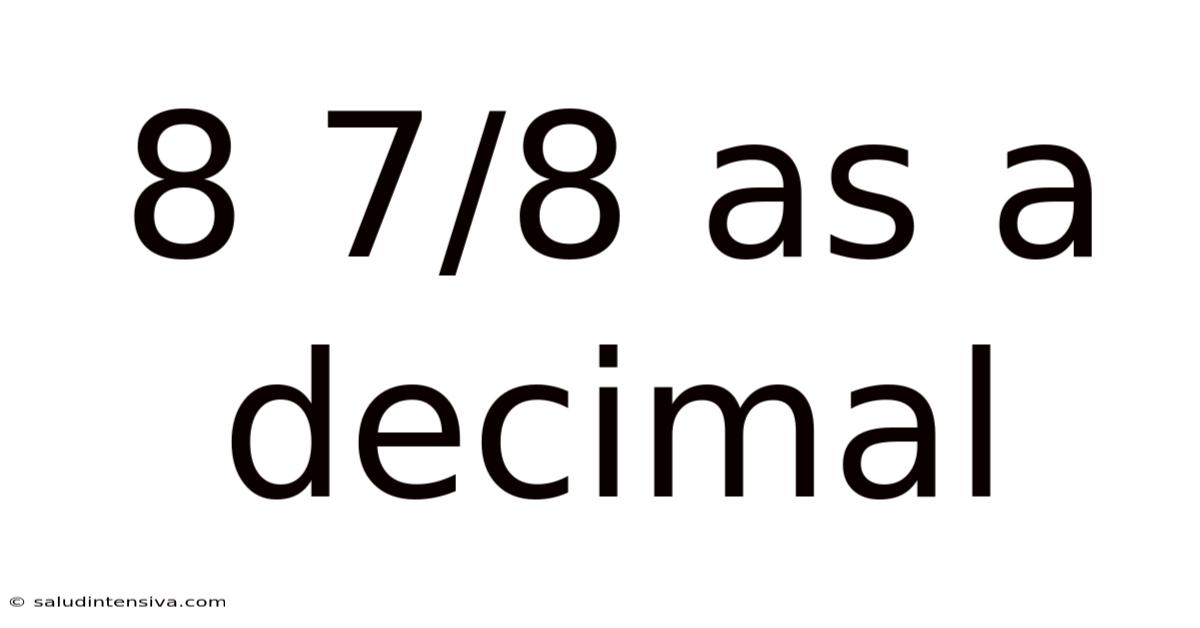
Table of Contents
8 7/8 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will explore the conversion of the mixed number 8 7/8 into its decimal equivalent, explaining the process in detail and covering various related concepts. Understanding this seemingly simple conversion will lay a solid foundation for tackling more complex fractional and decimal operations.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's briefly review the concepts of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 8 7/8. The whole number (8 in this case) represents a complete unit, while the fraction (7/8) represents a part of a unit. A fraction itself consists of a numerator (the top number, 7) and a denominator (the bottom number, 8). The denominator indicates how many equal parts a whole is divided into, and the numerator indicates how many of those parts are being considered.
Method 1: Converting the Fraction to a Decimal and Adding the Whole Number
This is the most straightforward approach. We'll first convert the fraction 7/8 into a decimal, then add the whole number 8.
1. Divide the Numerator by the Denominator:
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In our case, we divide 7 by 8:
7 ÷ 8 = 0.875
2. Add the Whole Number:
Now, add the whole number part (8) to the decimal equivalent of the fraction (0.875):
8 + 0.875 = 8.875
Therefore, 8 7/8 as a decimal is 8.875.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves an extra step but can be helpful in understanding the underlying relationship between fractions and decimals.
1. Convert the Mixed Number to an Improper Fraction:
To convert a mixed number to an improper fraction, we multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, while the denominator remains the same.
(8 x 8) + 7 = 64 + 7 = 71
So, 8 7/8 becomes the improper fraction 71/8.
2. Divide the Numerator by the Denominator:
Now, divide the numerator (71) by the denominator (8):
71 ÷ 8 = 8.875
Again, we arrive at the decimal equivalent of 8.875.
Understanding Decimal Places and Significance
The result, 8.875, has three decimal places. The first digit after the decimal point (8) represents tenths, the second (7) represents hundredths, and the third (5) represents thousandths. The number of decimal places indicates the precision of the decimal representation. In this case, 8.875 is a precise representation of 8 7/8.
Practical Applications of Decimal Conversion
Converting fractions to decimals is vital in many real-world situations:
-
Financial Calculations: Dealing with money often involves fractions of a dollar (cents). Converting fractions to decimals allows for accurate calculations of prices, discounts, interest rates, and more.
-
Measurements: Many measurement systems use both fractions and decimals. Converting between the two is essential for accurate calculations and comparisons of lengths, weights, volumes, etc.
-
Scientific Computations: In science and engineering, precise measurements and calculations are paramount. Converting fractions to decimals ensures accurate results in experiments, simulations, and data analysis.
-
Computer Programming: Computers primarily work with decimal numbers. Converting fractions to decimals is a necessary step in programming applications that involve fractional calculations.
Exploring Related Concepts: Recurring Decimals
While 8 7/8 converts to a terminating decimal (a decimal with a finite number of digits), not all fractions do. Some fractions result in recurring decimals, also known as repeating decimals. These are decimals where one or more digits repeat infinitely. For example, 1/3 = 0.3333... (the 3 repeats infinitely). Understanding the difference between terminating and recurring decimals is crucial for various mathematical operations.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to decimals?
A: Yes, all fractions can be converted to decimals. However, some will result in terminating decimals, while others will result in recurring decimals.
Q: What if I have a fraction with a large denominator?
A: The process remains the same: divide the numerator by the denominator. You might need a calculator for larger numbers to ensure accuracy.
Q: Is there a quicker way to convert fractions like 7/8 to decimals?
A: While the division method is always reliable, memorizing common fraction-to-decimal conversions (like 1/8 = 0.125, 1/4 = 0.25, 1/2 = 0.5, etc.) can speed up the process. You can then multiply these memorized values to obtain the decimal equivalent of other fractions. For example, since 1/8 = 0.125, then 7/8 = 7 * 0.125 = 0.875.
Q: Why is it important to learn to convert fractions to decimals?
A: It's crucial for accurate calculations in various fields, from finance and science to everyday tasks. It also improves your understanding of number systems and mathematical operations.
Conclusion
Converting 8 7/8 to its decimal equivalent, 8.875, is a straightforward process that involves either directly dividing the fractional part and adding the whole number or converting the mixed number to an improper fraction before dividing. Understanding this fundamental conversion is key to mastering various mathematical concepts and solving practical problems across numerous disciplines. While this example presents a terminating decimal, remember that not all fractions result in such neat conversions, and understanding recurring decimals is equally important for a complete understanding of this mathematical concept. Mastering this skill is a crucial step toward greater mathematical proficiency.
Latest Posts
Latest Posts
-
How Long Is 103 Minutes
Sep 16, 2025
-
What Is Half Of 31
Sep 16, 2025
-
5 1 4 As A Percent
Sep 16, 2025
-
1330 Military Time To Normal
Sep 16, 2025
-
Convert Mm To Sq Ft
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 8 7/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.