8 9 Divided By 4
saludintensiva
Sep 12, 2025 · 6 min read
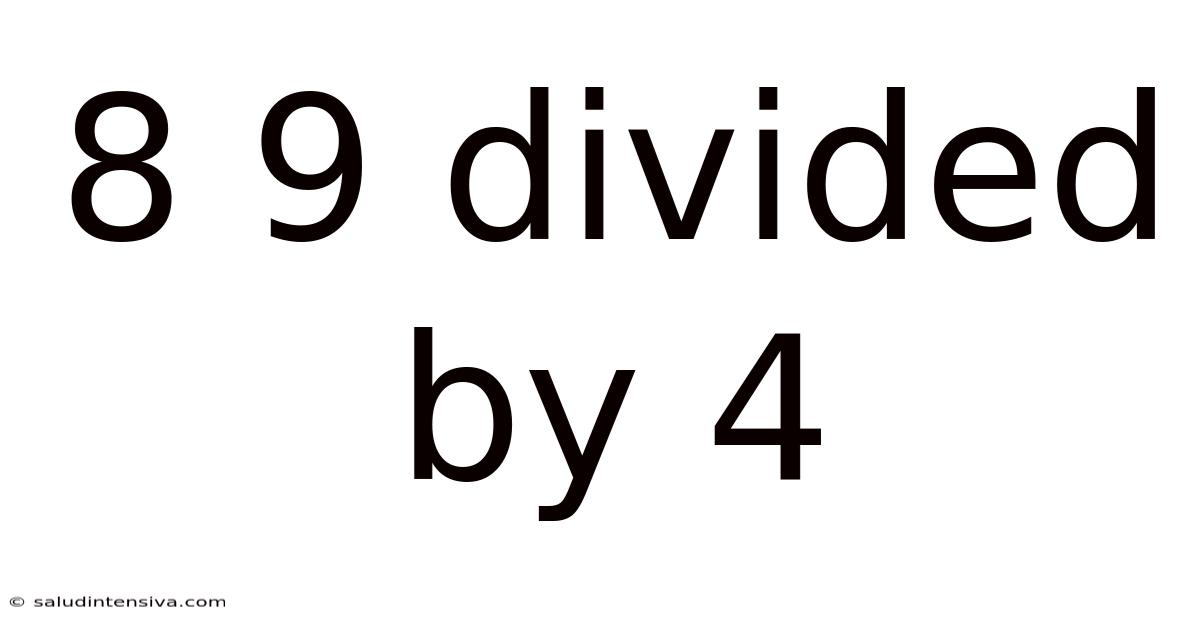
Table of Contents
Decoding 8 9/4: A Deep Dive into Mixed Numbers and Improper Fractions
This article explores the seemingly simple calculation of "8 9/4," delving beyond the immediate answer to provide a comprehensive understanding of mixed numbers, improper fractions, and their applications. We'll cover the conversion process, the underlying mathematical principles, and explore real-world scenarios where this type of calculation is relevant. This detailed explanation will not only provide the solution but also build a robust understanding of fractional arithmetic.
Understanding Mixed Numbers and Improper Fractions
Before we tackle 8 9/4, let's clarify the terminology. A mixed number combines a whole number and a fraction, like 8 9/4. An improper fraction, on the other hand, has a numerator (top number) that is greater than or equal to its denominator (bottom number). Understanding the relationship between these two forms is crucial for solving this problem and many others involving fractions.
For example, the mixed number 2 ¾ represents two whole units and three-quarters of another unit. Its equivalent improper fraction is 11/4 because it represents eleven quarters in total. This conversion is the key to solving problems like 8 9/4 efficiently and accurately.
Converting Mixed Numbers to Improper Fractions: A Step-by-Step Guide
Converting 8 9/4 from a mixed number to an improper fraction is the first step in solving the problem. Here's how it's done:
-
Multiply the whole number by the denominator: In our example, multiply 8 (the whole number) by 4 (the denominator). This gives us 32.
-
Add the numerator: Add the result from step 1 (32) to the numerator of the fraction (9). 32 + 9 = 41.
-
Keep the same denominator: The denominator remains unchanged. It stays as 4.
Therefore, the improper fraction equivalent of 8 9/4 is 41/4.
Solving 8 9/4 (or 41/4)
Now that we've converted 8 9/4 to its improper fraction form, we can perform any required mathematical operations. If the problem is simply to simplify the expression, we need to convert the improper fraction to a mixed number again. This involves division.
-
Divide the numerator by the denominator: Divide 41 by 4. This gives us a quotient of 10 and a remainder of 1.
-
Express as a mixed number: The quotient (10) becomes the whole number part of the mixed number. The remainder (1) becomes the numerator of the fraction, and the denominator remains 4.
Therefore, 41/4 simplifies to 10 1/4.
If, however, the problem involved further operations – such as addition, subtraction, multiplication, or division with other numbers – the improper fraction 41/4 would be the preferred form for easier calculations, especially if dealing with other fractions.
The Importance of Understanding Fractions in Everyday Life
Understanding fractions and their different forms isn't just confined to mathematics classrooms. Fractions play a vital role in various aspects of our daily lives:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients (e.g., ½ cup of sugar, ¾ teaspoon of salt). Accurate fraction understanding ensures consistent results.
-
Measurement and Construction: Carpentry, plumbing, and other construction trades heavily rely on fractional measurements (e.g., ½ inch, ⅛ inch) for precise work.
-
Finance and Budgeting: Understanding fractions is crucial for managing money effectively. Calculating percentages, discounts, and interest rates all involve fractional concepts.
-
Time Management: Telling time involves fractions of an hour (e.g., quarter past, half past). Efficient time management relies on an intuitive grasp of fractional time units.
-
Data Analysis and Statistics: Representing and analyzing data frequently requires fractional values and understanding the concept of proportions.
Expanding on Fractional Arithmetic: Further Exploration
The calculation of 8 9/4 serves as a springboard to explore more complex fractional arithmetic. Here are some relevant concepts to build upon:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. This often requires finding the least common multiple (LCM) of the denominators. For example: 1/2 + 1/4 = (2/4) + (1/4) = 3/4
-
Multiplying Fractions: Multiplying fractions is relatively straightforward. Multiply the numerators together, then multiply the denominators together. For example: (1/2) * (1/4) = 1/8
-
Dividing Fractions: To divide fractions, invert the second fraction (reciprocal) and then multiply. For example: (1/2) ÷ (1/4) = (1/2) * (4/1) = 4/2 = 2
Addressing Common Mistakes and Misconceptions
Several common mistakes arise when working with mixed numbers and improper fractions:
-
Incorrect conversion: The most frequent error is incorrectly converting a mixed number to an improper fraction or vice versa. Carefully following the steps outlined earlier is essential to avoid this.
-
Ignoring the denominator: Students might sometimes perform calculations on the numerators only, forgetting that the denominator also plays a crucial role.
-
Improper simplification: Failing to simplify fractions to their lowest terms (e.g., leaving 2/4 instead of simplifying to ½) leads to inaccurate results and a lack of precision.
-
Misunderstanding order of operations: When dealing with mixed numbers in more complex equations (e.g., involving addition, multiplication, division), students might forget the order of operations (PEMDAS/BODMAS).
Frequently Asked Questions (FAQ)
Q: What is the difference between a proper and an improper fraction?
A: A proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4), while an improper fraction has a numerator greater than or equal to the denominator (e.g., 5/4, 7/7).
Q: Why is it important to convert mixed numbers to improper fractions before performing calculations?
A: Converting to improper fractions simplifies calculations, especially when multiplying or dividing fractions. It eliminates the need to handle separate whole number and fractional components.
Q: Can I solve 8 9/4 directly without converting to an improper fraction?
A: While technically possible using a more complicated method involving separate calculations for the whole number and fractional part, converting to an improper fraction offers a more efficient and less error-prone method.
Q: Are there any real-world applications of this type of calculation beyond basic arithmetic?
A: Absolutely! Calculations involving mixed numbers and improper fractions are crucial in areas such as engineering, construction, finance, and even everyday activities like baking and cooking, as discussed earlier.
Q: How can I practice my skills in working with fractions?
A: Practice is key! Work through various problems involving adding, subtracting, multiplying, and dividing fractions and mixed numbers. Online resources and workbooks can provide ample practice opportunities.
Conclusion
This in-depth exploration of 8 9/4 highlights the importance of understanding mixed numbers and improper fractions. The seemingly simple problem reveals the underlying mathematical principles and practical applications of fractional arithmetic. Mastering these concepts is not only crucial for academic success but also essential for navigating many aspects of everyday life. By understanding the conversion process, the methods of solving such problems, and the broader applications, you've built a solid foundation for further exploration of fractional mathematics. Remember the steps involved, practice regularly, and you'll confidently tackle any fractional challenge that comes your way.
Latest Posts
Latest Posts
-
3 1 4 3 4
Sep 12, 2025
-
80 100 As A Decimal
Sep 12, 2025
-
Lcm Of 8 9 10
Sep 12, 2025
-
Greatest Common Factor Of 80
Sep 12, 2025
-
3 5 Is Equal To What
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 8 9 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.