8 Squared + 15 Squared
saludintensiva
Sep 12, 2025 · 5 min read
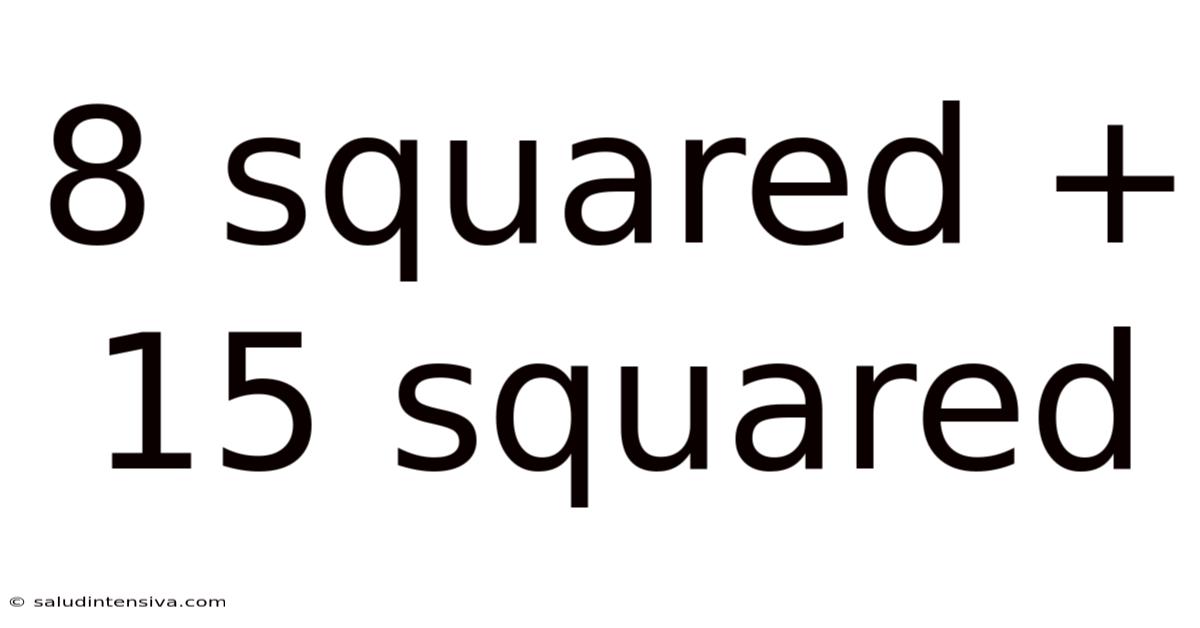
Table of Contents
Exploring the Mathematical Curiosity: 8 Squared + 15 Squared
This article delves into the seemingly simple mathematical expression "8 squared + 15 squared," uncovering its significance beyond a basic arithmetic problem. We will explore its calculation, its connection to Pythagorean triples, its applications in geometry, and even its potential for further mathematical exploration. This seemingly straightforward equation opens doors to a deeper understanding of fundamental mathematical concepts and their real-world implications. Understanding this expression provides a solid foundation for grasping more complex mathematical principles.
Understanding Squares and the Problem
Before diving into the intricacies of 8 squared + 15 squared, let's refresh our understanding of squares. In mathematics, squaring a number means multiplying it by itself. For example, 8 squared (written as 8²) is 8 x 8 = 64, and 15 squared (15²) is 15 x 15 = 225. Therefore, the problem 8² + 15² asks us to find the sum of these two squares: 64 + 225.
Performing the addition, we find that 64 + 225 = 289. So, the answer to 8 squared + 15 squared is 289. However, this simple calculation is just the starting point of a richer mathematical exploration.
The Connection to Pythagorean Triples
The result, 289, is itself a perfect square: 17 x 17 = 289 (or 17² = 289). This seemingly coincidental observation connects our problem to a crucial concept in mathematics: Pythagorean triples.
A Pythagorean triple is a set of three positive integers (a, b, c) that satisfy the Pythagorean theorem: a² + b² = c². The Pythagorean theorem is fundamental to geometry, describing the relationship between the sides of a right-angled triangle: the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs).
In our case, we have a² = 64 (a = 8), b² = 225 (b = 15), and c² = 289 (c = 17). This means that (8, 15, 17) forms a Pythagorean triple. This triple represents the lengths of the sides of a right-angled triangle: a leg of length 8, a leg of length 15, and a hypotenuse of length 17.
This connection to the Pythagorean theorem demonstrates that the seemingly simple arithmetic problem we started with has deep geometric implications. It highlights the interconnectedness of different mathematical branches – arithmetic and geometry – and how seemingly unrelated concepts can converge to reveal profound relationships.
Geometric Interpretation and Applications
The Pythagorean triple (8, 15, 17) has practical applications in various fields. Consider the construction industry: a right-angled triangle with sides measuring 8, 15, and 17 units can be used to ensure accurate measurements during building projects, especially when laying foundations or constructing walls at precise right angles. This is just one example of how the practical application of a mathematical concept, like the Pythagorean theorem, can translate into real-world solutions.
Furthermore, the concept of Pythagorean triples extends beyond simple right-angled triangles. They are used in advanced areas of mathematics such as number theory, cryptography, and even computer graphics. Understanding the fundamental principle behind these triples provides a strong base for tackling more complex mathematical problems in these fields.
Generating Pythagorean Triples: Beyond 8, 15, 17
The Pythagorean triple (8, 15, 17) is just one example. There are infinitely many such triples. While finding them through trial and error is possible, more systematic methods exist. One common method involves using Euclid's formula:
- a = m² - n²
- b = 2mn
- c = m² + n²
Where 'm' and 'n' are any two positive integers, with 'm' being greater than 'n'. By substituting different values of 'm' and 'n', you can generate different Pythagorean triples. For instance, if m = 4 and n = 1, we get:
- a = 4² - 1² = 15
- b = 2 * 4 * 1 = 8
- c = 4² + 1² = 17
This gives us our (8, 15, 17) triple, albeit in a slightly different order. Experimenting with different values of 'm' and 'n' allows you to explore the vast landscape of Pythagorean triples and appreciate the underlying mathematical structure.
Advanced Mathematical Concepts and Further Exploration
The exploration of 8² + 15² opens doors to more complex mathematical concepts. For instance, understanding perfect squares and their properties is crucial in number theory. Further investigation might involve exploring Fermat's Last Theorem, a famous theorem in number theory that extends the concept of Pythagorean triples to higher powers. While Fermat's Last Theorem is significantly more complex, the familiarity with Pythagorean triples gained from understanding 8² + 15² provides a valuable conceptual foundation.
Frequently Asked Questions (FAQ)
-
Q: Is 289 the only result of adding two squares? A: No, there are infinitely many pairs of numbers whose squares add up to another perfect square (or not). This is related to the infinite number of Pythagorean triples.
-
Q: Are all Pythagorean triples integers? A: Yes, by definition, a Pythagorean triple consists of three positive integers.
-
Q: What is the significance of the Pythagorean theorem? A: The Pythagorean theorem is fundamental to geometry and trigonometry. It defines the relationship between the sides of a right-angled triangle and has applications in various fields, from construction to advanced physics.
-
Q: How can I find more Pythagorean triples? A: Use Euclid's formula (explained above) or explore online resources and mathematical texts dedicated to number theory.
Conclusion
The seemingly simple problem of calculating 8² + 15² opens a fascinating window into the world of mathematics. It illustrates the power of seemingly basic arithmetic, revealing its deep connections to geometry through the Pythagorean theorem and Pythagorean triples. From its practical applications in construction to its role in more advanced mathematical concepts, this problem underscores the interconnectedness and beauty of mathematics. The journey of exploring this simple equation leads to a deeper appreciation of the underlying principles and the boundless possibilities within the mathematical world. It encourages further exploration and highlights how even the most elementary mathematical expressions can contain rich mathematical significance.
Latest Posts
Latest Posts
-
Percent Change With Negative Numbers
Sep 13, 2025
-
What Time Is 14 35
Sep 13, 2025
-
How To Find Avg Velocity
Sep 13, 2025
-
29 30 As A Decimal
Sep 13, 2025
-
Gcf For 12 And 48
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 8 Squared + 15 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.