9 16 In Simplest Form
saludintensiva
Sep 17, 2025 · 6 min read
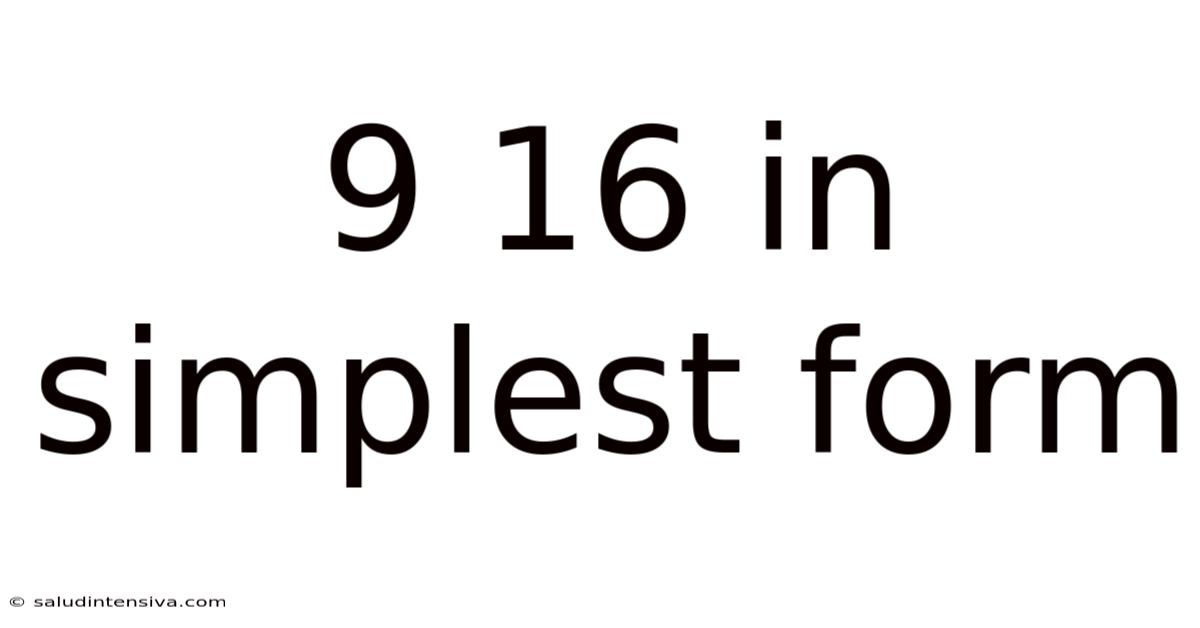
Table of Contents
Simplifying Fractions: A Deep Dive into 9/16
Understanding fractions is fundamental to mathematics, forming the building blocks for more advanced concepts like algebra, calculus, and beyond. This article explores the simplification of fractions, using the example of 9/16 to illustrate the process and delve into the underlying mathematical principles. We'll cover various methods, explore the concept of greatest common divisors (GCD), and answer frequently asked questions to provide a comprehensive understanding of fraction simplification.
Introduction: What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 9/16, 9 is the numerator and 16 is the denominator. This means we have 9 parts out of a total of 16 equal parts. Simplifying a fraction means reducing it to its lowest terms, finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and work with.
Understanding the Concept of Simplification
Simplifying a fraction doesn't change its value; it simply represents the same value in a more concise form. Think of it like this: a half (1/2) is the same as two quarters (2/4) or four eighths (4/8). All these fractions represent the same portion of a whole, but 1/2 is the simplest form. The goal of simplification is to find this simplest form.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Once we find the GCD, we divide both the numerator and denominator by it to get the simplified fraction.
Let's apply this to 9/16:
- Find the factors of 9: 1, 3, 9
- Find the factors of 16: 1, 2, 4, 8, 16
- Identify the common factors: The only common factor of 9 and 16 is 1.
Since the GCD of 9 and 16 is 1, the fraction 9/16 is already in its simplest form. We cannot simplify it further.
Method 2: Prime Factorization
Another approach to finding the GCD is using prime factorization. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
Comparing the prime factorizations, we see there are no common prime factors between 9 and 16. Therefore, the GCD is 1, confirming that 9/16 is already in its simplest form.
Why 9/16 Cannot Be Simplified Further
The fraction 9/16 is considered an irreducible fraction because its numerator and denominator share no common factors other than 1. This means it's in its simplest form and cannot be reduced any further. Attempting to divide both the numerator and denominator by any number other than 1 will result in a fraction that is not equivalent to 9/16.
Visual Representation of 9/16
Imagine a square divided into 16 equal parts. Shading 9 of those parts would visually represent the fraction 9/16. There's no way to group these shaded parts into larger, equal groups to simplify the representation further. This visual reinforces the concept that 9/16 is already in its simplest form.
Comparing Fraction Simplification Methods
Both the GCD method and the prime factorization method achieve the same result – determining whether a fraction can be simplified and, if so, simplifying it to its lowest terms. The prime factorization method is particularly useful for larger numbers where finding all the factors can be time-consuming. However, for smaller numbers like 9 and 16, the GCD method is often quicker and easier.
Practical Applications of Fraction Simplification
Simplifying fractions is crucial in various real-world applications:
- Cooking and Baking: Recipes often require fractions of ingredients. Simplifying fractions ensures accurate measurements.
- Construction and Engineering: Precise measurements and calculations are essential in construction and engineering, and simplifying fractions contributes to accuracy.
- Finance: Dealing with fractions of money (like calculating interest or discounts) requires understanding and simplifying fractions.
- Data Analysis: Simplifying fractions can improve the clarity and readability of data presented in charts and graphs.
Expanding on the Concept: Equivalent Fractions
While 9/16 is in its simplest form, it has many equivalent fractions. An equivalent fraction represents the same value as the original fraction. We can create equivalent fractions by multiplying both the numerator and the denominator by the same number. For example:
- 18/32 (multiplying both by 2)
- 27/48 (multiplying both by 3)
- 36/64 (multiplying both by 4)
All these fractions are equivalent to 9/16, but 9/16 is the simplest representation.
Frequently Asked Questions (FAQ)
-
Q: What if I accidentally simplify a fraction incorrectly?
A: To check your work, you can always perform the division of the numerator by the denominator for both the original and simplified fraction. If they produce the same decimal value, your simplification is correct.
-
Q: Are there any shortcuts for simplifying fractions?
A: While there aren't significant shortcuts for all fractions, recognizing easily divisible pairs (e.g., multiples of 2, 5, or 10) can speed up the process.
-
Q: How can I improve my skills in simplifying fractions?
A: Practice is key. Work through various examples, using different methods to gain proficiency. Focus on understanding the underlying concepts rather than simply memorizing steps.
-
Q: What if the numerator is larger than the denominator?
A: This is an improper fraction. You can simplify it in the same way as a proper fraction, and then convert it to a mixed number (a whole number and a proper fraction) if needed. For example, 16/9 simplifies to itself (it's already in lowest terms), but you can express it as the mixed number 1 7/9.
-
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It improves clarity and accuracy in mathematical problems and real-world applications.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics. By understanding the concepts of GCD, prime factorization, and equivalent fractions, you can confidently simplify any fraction. The ability to simplify fractions efficiently not only improves your mathematical skills but also enhances your problem-solving abilities across various fields. Remember that the key is to practice consistently and strive for a deep conceptual understanding, rather than just memorizing procedures. Through consistent effort and practice, you can master this important mathematical skill and use it with confidence.
Latest Posts
Latest Posts
-
Gcf Of 18 And 50
Sep 17, 2025
-
First 10 Multiples Of 7
Sep 17, 2025
-
How Long Is 280 Minutes
Sep 17, 2025
-
Multiples Of 6 To 100
Sep 17, 2025
-
Percent Difference Formula Experimental Theoretical
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 9 16 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.