9 16 To 4 5
saludintensiva
Sep 21, 2025 · 6 min read
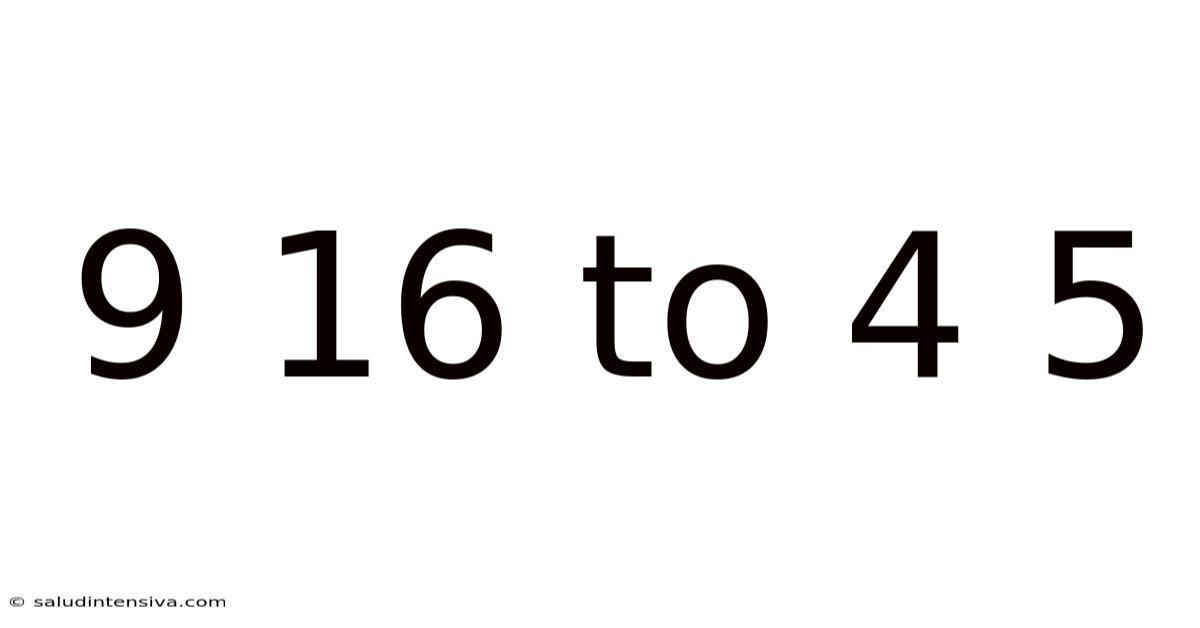
Table of Contents
Decoding the Enigma: From 9/16 to 4/5 – A Journey Through Fractions, Ratios, and Proportions
This article delves into the fascinating relationship between the fractions 9/16 and 4/5, exploring their mathematical properties, practical applications, and the underlying concepts of ratios and proportions. We'll unpack these seemingly simple fractions, revealing the rich mathematical landscape they represent. Understanding these concepts is crucial for various fields, from basic arithmetic to advanced engineering and scientific calculations. Whether you're a student grappling with fractions or a curious individual seeking a deeper understanding of mathematics, this guide will illuminate the pathway from 9/16 to 4/5 and beyond.
Introduction: Understanding Fractions and Their Significance
Fractions represent parts of a whole. They are expressed as a ratio of two integers: a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts, while the numerator specifies how many of those parts are being considered. For example, in the fraction 9/16, the denominator (16) tells us the whole is divided into 16 equal parts, and the numerator (9) indicates that we are considering 9 of those parts. Similarly, 4/5 represents 4 out of 5 equal parts. Understanding fractions is foundational to grasping more complex mathematical concepts.
Comparing 9/16 and 4/5: A Direct Approach
At first glance, comparing 9/16 and 4/5 might seem straightforward. However, a direct comparison requires finding a common denominator, a number divisible by both 16 and 5. The least common multiple (LCM) of 16 and 5 is 80. Therefore, we convert both fractions to have a denominator of 80:
- 9/16 = (9 x 5) / (16 x 5) = 45/80
- 4/5 = (4 x 16) / (5 x 16) = 64/80
Now, the comparison is clear: 64/80 > 45/80, meaning 4/5 is greater than 9/16.
Exploring the Ratio and Proportion Perspective
The relationship between 9/16 and 4/5 can also be understood through the lens of ratios and proportions. A ratio expresses the relative size of two quantities. In this case, we can express the ratio of 9/16 to 4/5 as 9/16 : 4/5. To simplify this ratio, we can multiply both sides by the least common multiple of the denominators (80):
(9/16) * 80 : (4/5) * 80 = 45 : 64
This simplified ratio confirms our earlier finding: 45 is smaller than 64. A proportion, on the other hand, is a statement of equality between two ratios. While 9/16 and 4/5 are not equal, we can explore proportions involving these fractions in various contexts. For instance, we might ask: "If 9 parts represent x, and 16 parts represent y, and 4 parts represent z, and 5 parts represent w, what is the relationship between x, y, z, and w?"
Decimals and Percentages: Alternative Representations
Converting fractions to decimals and percentages offers another perspective.
- 9/16 = 0.5625
- 4/5 = 0.8
Expressing them as percentages:
- 9/16 = 56.25%
- 4/5 = 80%
This clearly demonstrates that 4/5 (80%) is significantly larger than 9/16 (56.25%). These decimal and percentage representations are often more intuitive for practical applications.
Practical Applications: Real-World Scenarios
The fractions 9/16 and 4/5 appear in various real-world situations. For example:
- Measurements: 9/16 inch might represent a specific dimension in engineering or woodworking, while 4/5 of a liter might be a measurement in a recipe. Understanding their relative sizes is crucial for accurate measurements.
- Proportions in recipes: If a recipe calls for 9/16 of a cup of flour and you want to increase the recipe's size proportionally, you'd need to maintain the same ratio.
- Probability: These fractions could represent probabilities in various scenarios. For instance, the probability of a certain event occurring could be 9/16, while another event's probability could be 4/5. Understanding the relative likelihoods is crucial for decision-making.
- Data Analysis: In statistical analysis, these fractions could represent proportions within a dataset. For example, 9/16 of a sample might exhibit a particular characteristic, while 4/5 of another sample shows a different characteristic. Analyzing these proportions helps draw meaningful conclusions.
Mathematical Operations with 9/16 and 4/5
Let's explore some basic mathematical operations involving these fractions:
- Addition: 9/16 + 4/5 = (45/80) + (64/80) = 109/80 = 1 and 29/80
- Subtraction: 4/5 - 9/16 = (64/80) - (45/80) = 19/80
- Multiplication: (9/16) * (4/5) = 36/80 = 9/20
- Division: (4/5) / (9/16) = (4/5) * (16/9) = 64/45 = 1 and 19/45
These operations highlight the importance of finding common denominators for addition and subtraction, while multiplication and division involve simpler calculations.
Further Exploration: Extending the Concepts
The comparison and manipulation of 9/16 and 4/5 serve as a springboard for exploring more advanced mathematical concepts.
- Continued Fractions: Both fractions can be represented as continued fractions, providing alternative ways to express and approximate their values.
- Approximations: Understanding how to approximate fractions is crucial in practical situations where exact values may not be necessary.
- Series and Sequences: These fractions could be incorporated into various series and sequences, leading to explorations in calculus and analysis.
- Geometric and Arithmetic Progressions: Understanding how these fractions behave within geometric or arithmetic progressions can illuminate their properties in a wider mathematical context.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 9/16?
A: 9/16 is already in its simplest form, as 9 and 16 share no common factors other than 1.
Q: How do I convert 9/16 to a decimal?
A: Divide 9 by 16 using long division or a calculator, resulting in 0.5625.
Q: How do I convert 4/5 to a percentage?
A: Multiply 4/5 by 100%: (4/5) * 100% = 80%
Q: Are there any real-world examples where these fractions are commonly used?
A: Yes, as mentioned earlier, they're used in measurements (e.g., inches, liters), recipes, and probability calculations.
Q: Which fraction, 9/16 or 4/5, is closer to 1/2?
A: 9/16 (0.5625) is closer to 1/2 (0.5) than 4/5 (0.8).
Conclusion: A Deeper Appreciation of Fractions
This exploration of the relationship between 9/16 and 4/5 has revealed the multifaceted nature of fractions. Beyond simple arithmetic, these fractions serve as building blocks for understanding ratios, proportions, decimals, percentages, and more advanced mathematical concepts. By examining these seemingly simple fractions, we've uncovered a pathway to a richer appreciation of the elegance and practicality of mathematics in our daily lives. The ability to confidently work with fractions is a valuable skill applicable across various disciplines, from everyday tasks to complex scientific endeavors. Remember, the journey from 9/16 to 4/5, and beyond, is a journey of continuous learning and discovery.
Latest Posts
Latest Posts
-
Square Root Transformation In Statistics
Sep 21, 2025
-
Bullet Points Inside Excel Cell
Sep 21, 2025
-
25 24 As A Decimal
Sep 21, 2025
-
2 1 As A Mixed Number
Sep 21, 2025
-
How To Measure 20 Meters
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 9 16 To 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.