9 20 As A Percent
saludintensiva
Sep 10, 2025 · 5 min read
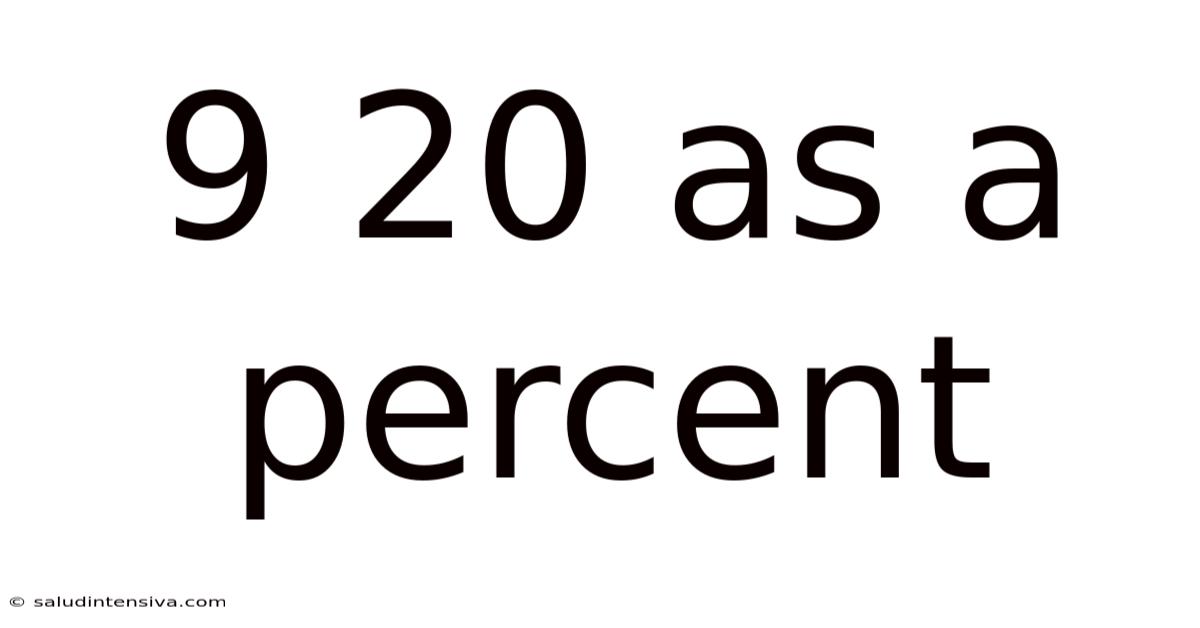
Table of Contents
9/20 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday budgeting to complex scientific calculations. This article provides a comprehensive guide to converting the fraction 9/20 into a percentage, explaining the process step-by-step and exploring related concepts. We'll delve into the underlying principles, offer multiple solution methods, and address frequently asked questions to ensure a complete understanding of this important topic.
Understanding Fractions and Percentages
Before diving into the conversion, let's clarify the basics. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 9/20, 9 is the numerator and 20 is the denominator. This means we're considering 9 parts out of a total of 20 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion relative to 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: The Direct Conversion Method
This method involves directly converting the fraction 9/20 into a decimal and then into a percentage.
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (9) by the denominator (20):
9 ÷ 20 = 0.45
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.45 × 100 = 45%
Therefore, 9/20 is equal to 45%.
Method 2: The Equivalent Fraction Method
This method involves finding an equivalent fraction with a denominator of 100.
Step 1: Find the equivalent fraction.
We need to find a number that, when multiplied by 20 (the denominator), equals 100. This number is 5 (because 20 x 5 = 100). To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same number:
(9 x 5) / (20 x 5) = 45/100
Step 2: Convert the equivalent fraction to a percentage.
Since a percentage is a fraction out of 100, 45/100 directly translates to 45%.
Therefore, 9/20 is equal to 45%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage.
We can set up a proportion:
9/20 = x/100
Where 'x' represents the percentage we're trying to find.
To solve for x, we cross-multiply:
20x = 900
Then, divide both sides by 20:
x = 900 ÷ 20 = 45
Therefore, x = 45%, so 9/20 is equal to 45%.
Understanding the Result: 45%
The result, 45%, signifies that 9 out of 20 parts represent 45 out of 100 parts. This means that 9/20 represents 45% of the whole. This percentage can be applied in various contexts:
- In a classroom: If 20 students are in a class and 9 of them passed an exam, the pass rate is 45%.
- In sales: If a store aims to sell 20 units of a product and has sold 9, they have achieved 45% of their sales goal.
- In finance: If you have invested $20 and earned a profit of $9, your return on investment is 45%.
Further Applications and Extensions
The understanding of converting fractions to percentages extends beyond simple calculations. Here are some advanced applications:
- Calculating discounts: A 45% discount on a $100 item means a reduction of $45 (45% of $100).
- Determining tax rates: A sales tax of 45% on a $50 purchase would be an additional $22.50 (45% of $50).
- Analyzing data: Percentages are fundamental in interpreting statistical data, presenting results visually (e.g., pie charts), and comparing different sets of data.
- Solving percentage problems: Understanding this conversion allows you to tackle a wide range of percentage-based word problems effectively. For instance, you could easily calculate what percentage 18 represents out of 40 using similar conversion methods.
Frequently Asked Questions (FAQ)
Q1: Why is it important to know how to convert fractions to percentages?
A1: Converting fractions to percentages allows for easier comparison and interpretation of different proportions. Percentages provide a standardized way of expressing parts of a whole, making it easier to understand and communicate quantitative information.
Q2: Are there other methods for converting fractions to percentages?
A2: While the methods discussed are the most common, you can also use calculators or online converters designed specifically for fraction-to-percentage conversions. Some advanced calculators can handle complex fraction conversions directly.
Q3: What if the fraction has a decimal in the numerator or denominator?
A3: You can still apply the same methods. First, convert any decimal components to fractions. Then, proceed with the conversion using any of the described methods.
Q4: What if the fraction is an improper fraction (numerator > denominator)?
A4: Convert the improper fraction into a mixed number (a whole number and a fraction). Then convert the fractional part to a decimal and then to a percentage, finally adding the whole number component. For example, if you had 29/20, this would be 1 and 9/20, making it 145% (1 + 45%).
Q5: Can percentages exceed 100%?
A5: Yes, percentages can exceed 100%. This occurs when the numerator of the fraction is larger than the denominator, indicating that the part is greater than the whole. This often happens in scenarios involving growth or increase, like population growth or investment returns exceeding the initial amount.
Conclusion
Converting 9/20 to a percentage is a straightforward process that can be accomplished using several methods. Understanding these methods not only provides a solution to a specific problem but also strengthens your overall understanding of fractions, decimals, and percentages—essential mathematical concepts applicable across numerous fields. The ability to perform this conversion proficiently is a valuable skill for both academic and practical applications, enhancing your problem-solving capabilities and your ability to interpret and communicate quantitative information effectively. Remember to practice these methods to build confidence and fluency in handling similar conversions in the future. The more you practice, the easier and more intuitive this process will become.
Latest Posts
Latest Posts
-
26 Acres To Sq Ft
Sep 10, 2025
-
Dividing Fractions By Whole Numbers
Sep 10, 2025
-
Gcf Of 28 And 36
Sep 10, 2025
-
How To Compute Floor Area
Sep 10, 2025
-
Lowest Common Multiple Of 24
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 9 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.