A Cubed + B Cubed
saludintensiva
Sep 20, 2025 · 5 min read
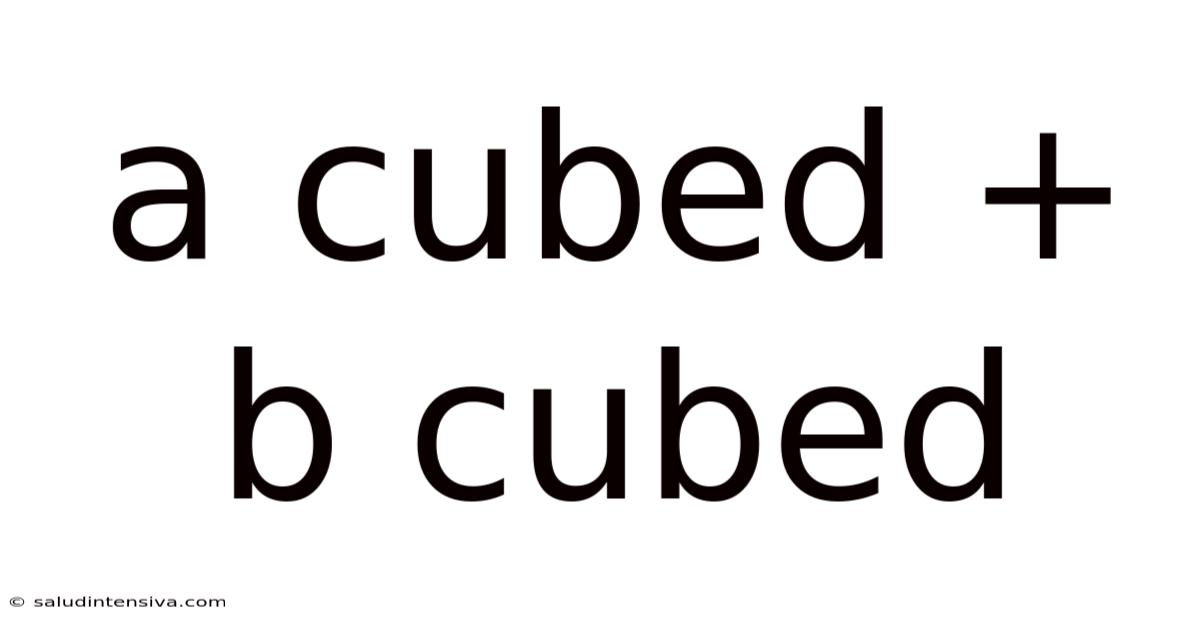
Table of Contents
Decoding the Mystery: A Cubed Plus B Cubed (a³ + b³)
Understanding the mathematical expression a³ + b³ might seem daunting at first glance, but it's a fundamental concept with significant applications in various fields, from algebra to calculus and beyond. This comprehensive guide will delve into the intricacies of a³ + b³, exploring its factorization, geometric interpretation, and practical applications, ensuring a thorough understanding for readers of all levels. We'll break down the complexities into easily digestible steps, making this seemingly complex topic accessible and engaging.
Introduction: Understanding the Basics
The expression a³ + b³ represents the sum of two cubes, where 'a' and 'b' are any real numbers. This seemingly simple expression holds a wealth of mathematical properties and reveals elegant solutions when approached systematically. This article will not only explain how to factor a³ + b³ but will also provide a deeper understanding of its underlying principles and diverse applications. Mastering this concept is a cornerstone for further exploration in advanced mathematical concepts.
Factorization of a³ + b³: The Sum of Cubes Formula
The key to unlocking the secrets of a³ + b³ lies in its factorization. Unlike the difference of squares (a² - b²), which factors neatly into (a + b)(a - b), the sum of cubes has a slightly more complex factorization. The formula is:
a³ + b³ = (a + b)(a² - ab + b²)
This factorization is crucial for simplifying expressions, solving equations, and tackling more complex mathematical problems. Let's break down this formula step-by-step:
- (a + b): This is a simple binomial representing the sum of 'a' and 'b'.
- (a² - ab + b²): This is a trinomial, a polynomial with three terms. It's important to note that this trinomial generally cannot be factored further using real numbers.
Proof of the Factorization:
To verify the factorization, we can expand the expression (a + b)(a² - ab + b²):
a(a² - ab + b²) + b(a² - ab + b²) = a³ - a²b + ab² + a²b - ab² + b³
Notice that the terms -a²b and +a²b cancel each other out, as do +ab² and -ab². This leaves us with:
a³ + b³
Thus, proving the validity of the factorization formula.
Geometric Interpretation: Visualizing Cubes
The sum of cubes can also be visualized geometrically. Imagine two cubes, one with side length 'a' and the other with side length 'b'. The expression a³ + b³ represents the total volume of both cubes combined. While this doesn't directly lead to the factorization, it provides an intuitive understanding of the concept. The geometric interpretation emphasizes the additive nature of the expression, highlighting that we are combining two distinct volumes. This visual representation can be particularly helpful for those who are visually oriented learners.
Step-by-Step Examples: Applying the Formula
Let's illustrate the application of the formula with a few examples:
Example 1: Simple Numbers
Factorize 8³ + 27³.
Here, a = 8 and b = 27. Therefore:
8³ + 27³ = (8 + 27)(8² - 8*27 + 27²) = (35)(64 - 216 + 729) = 35 * 577 = 20195
Example 2: Variables
Factorize x³ + y³.
In this case, a = x and b = y. The factorization is straightforward:
x³ + y³ = (x + y)(x² - xy + y²)
Example 3: More Complex Expressions
Factorize (2x)³ + (3y)³.
Here, a = 2x and b = 3y. Applying the formula:
(2x)³ + (3y)³ = (2x + 3y)((2x)² - (2x)(3y) + (3y)²) = (2x + 3y)(4x² - 6xy + 9y²)
Applications of a³ + b³: Beyond the Textbook
The sum of cubes formula isn't just a theoretical concept; it has practical applications in various areas of mathematics and beyond:
-
Solving Cubic Equations: The factorization can be instrumental in solving certain types of cubic equations. By recognizing the sum of cubes pattern, we can simplify the equation and find its roots more efficiently.
-
Calculus: In calculus, the sum of cubes factorization is used in integration and differentiation problems, simplifying complex expressions to allow for easier manipulation.
-
Geometry and Volume Calculations: As mentioned earlier, the geometric interpretation allows us to calculate volumes of combined shapes.
-
Engineering and Physics: The formula can appear in various engineering and physics problems related to volume, displacement, and other three-dimensional phenomena.
Advanced Topics: Further Exploration
For those seeking a more in-depth understanding, here are some advanced topics related to the sum of cubes:
-
Complex Numbers: The formula can be extended to include complex numbers, expanding its applicability to a wider range of mathematical problems.
-
Higher-Order Polynomials: While we've focused on the sum of two cubes, similar factorization techniques can be applied to higher-order polynomials, showcasing the versatility of the underlying principles.
-
Relationship to Other Mathematical Concepts: Exploring the connections between the sum of cubes and other mathematical concepts, such as geometric series and binomial theorem, can deepen your understanding of mathematical interrelationships.
Frequently Asked Questions (FAQ)
-
Can a³ + b³ always be factored? Yes, using real numbers, a³ + b³ can always be factored into (a + b)(a² - ab + b²).
-
Is the trinomial (a² - ab + b²) always prime? Generally, yes, the trinomial (a² - ab + b²) cannot be factored further using real numbers unless specific conditions are met. However, it can be factored further using complex numbers.
-
What if a and b are negative numbers? The formula still applies. Just remember to handle the signs carefully during the calculations.
-
Are there alternative methods for factoring a³ + b³? While the standard formula is most efficient, other methods might exist depending on the context.
Conclusion: Mastering the Sum of Cubes
The sum of cubes, a³ + b³, is more than just a mathematical expression; it's a gateway to understanding deeper concepts in algebra, calculus, and beyond. This article has explored its factorization, geometric interpretation, and practical applications, equipping you with the knowledge and tools to tackle a wider range of mathematical problems. Remember the key formula: a³ + b³ = (a + b)(a² - ab + b²), and practice applying it to various examples. Through consistent practice and exploration, you'll not only master the sum of cubes but also enhance your overall mathematical proficiency. By understanding the core principles and exploring its diverse applications, you will be well-equipped to handle more complex mathematical challenges with confidence. The journey of mathematical discovery is ongoing, and mastering the sum of cubes is a significant step in that journey.
Latest Posts
Latest Posts
-
8 40 As A Percent
Sep 20, 2025
-
4 Way Venn Diagram Generator
Sep 20, 2025
-
Is 28 A Rational Number
Sep 20, 2025
-
How High Is 20 M
Sep 20, 2025
-
Calculating Using Significant Figures Worksheet
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about A Cubed + B Cubed . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.