Cube Root Of X 2
saludintensiva
Sep 19, 2025 · 6 min read
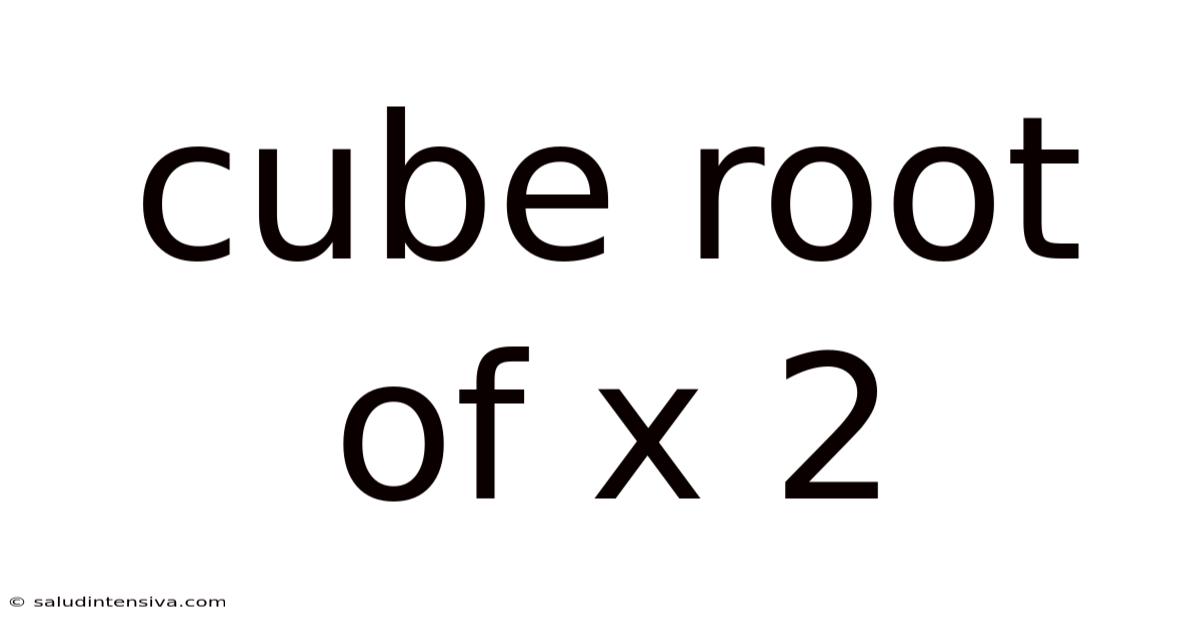
Table of Contents
Unveiling the Mysteries of the Cube Root of x²: A Comprehensive Guide
The cube root of x², often represented as ³√(x²), might seem like a straightforward mathematical concept, but it holds a surprising depth and relevance across various fields. This comprehensive guide will delve into its meaning, calculation methods, properties, and applications, ensuring a clear understanding for readers of all mathematical backgrounds. We'll explore both the theoretical underpinnings and practical implications, offering a complete picture of this fundamental concept. Understanding the cube root of x² is essential for anyone working with algebra, calculus, geometry, and even certain aspects of physics and engineering.
Understanding the Fundamentals: What is the Cube Root of x²?
Before diving into complex calculations, let's establish a solid foundation. The cube root of a number is the value that, when multiplied by itself three times, yields the original number. For example, the cube root of 8 is 2 because 2 x 2 x 2 = 8. Similarly, the cube root of x² represents the number that, when cubed (multiplied by itself three times), equals x². It's important to note that this differs from simply squaring x and then taking the cube root; it involves finding the number that, when cubed, results in x².
Calculating the Cube Root of x²: Methods and Approaches
Calculating the cube root of x² can be approached in several ways, depending on the context and the tools available.
1. Numerical Methods: For specific numerical values of x, we can use calculators or computer software to directly compute ³√(x²). Most scientific calculators have a cube root function (often denoted as ³√ or x^(1/3)). Simply input the square of x and then apply the cube root function.
2. Algebraic Manipulation: If x is represented algebraically, manipulating the expression might simplify the calculation. This approach is particularly useful when dealing with equations or expressions involving x². However, it's important to remember that the cube root of x² cannot be simplified further in terms of basic algebraic operations. There is no algebraic simplification of ³√(x²). The expression itself is the most simplified form.
3. Approximations: In situations where an exact value is not crucial, approximation techniques can be employed. These methods, such as linear approximation or iterative methods (like the Newton-Raphson method), provide estimates of the cube root. However, the accuracy of these approximations depends on the method used and the desired level of precision.
Exploring the Properties of ³√(x²)
The cube root of x² shares some properties with other roots and powers. Understanding these properties is crucial for manipulating and solving problems involving this expression.
-
Non-negativity: For real numbers x, the cube root of x² is always non-negative. This is because squaring a number always results in a non-negative value, and the cube root of a non-negative number is also non-negative.
-
Even Function: The function f(x) = ³√(x²) is an even function. An even function is symmetric with respect to the y-axis, meaning f(-x) = f(x). This implies that the cube root of (-x)² is the same as the cube root of x², since (-x)² = x².
-
Relationship to other functions: The cube root of x² is closely related to other mathematical functions. For instance, it can be expressed as x^(2/3). This representation highlights its connection to fractional exponents and power functions. This allows for easier manipulation using the rules of exponents. For example, (³√(x²))³ = x².
-
Domain and Range: The domain of the function f(x) = ³√(x²) is all real numbers, (-∞, ∞). This is because you can square any real number. The range of this function is also all non-negative real numbers, [0, ∞).
Applications of the Cube Root of x² in Real-World Scenarios
While the cube root of x² might seem abstract, it finds practical applications in various fields.
1. Geometry and Volume Calculations: Consider a cube with side length x. Its volume is x³. If we are given the surface area of one face (x²), finding the cube root of this area helps us determine the side length, which allows us to calculate the volume. This applies to many volume calculations involving cubes or shapes related to cubes. Similarly, if dealing with volumes proportional to x², finding the cube root relates the volume to the relevant linear dimension.
2. Physics and Engineering: The cube root of x² appears in various physical formulas, particularly those involving relationships between volume, surface area, and other physical properties. For instance, problems related to heat transfer, fluid dynamics, and material science may involve this expression in their calculations. This may involve estimations or approximations due to the complexity of real world phenomena.
3. Data Analysis and Statistics: Although less common than other statistical functions, the cube root of x² may be employed in certain statistical transformations or normalization procedures to ensure better distribution for analysis. This might be relevant when dealing with squared deviations or variances within datasets.
Advanced Concepts and Extensions
For those seeking a deeper understanding, here are some advanced considerations related to the cube root of x².
1. Complex Numbers: When extending the concept to complex numbers, the cube root of x² has multiple solutions due to the nature of complex roots. Each solution corresponds to a different phase angle in the complex plane.
2. Calculus: The derivative and integral of ³√(x²) can be evaluated using the rules of calculus. Understanding these derivatives and integrals is important in the application of calculus to more complex equations and models that use the expression ³√(x²).
3. Fractional Calculus: The concept can be extended into the realm of fractional calculus, where derivatives and integrals of non-integer orders are considered. This involves more advanced mathematical tools and methods.
Frequently Asked Questions (FAQs)
Q: Can the cube root of x² be simplified further?
A: No, ³√(x²) is already in its simplest algebraic form for real numbers.
Q: What is the difference between ³√(x²) and (³√x)²?
A: They are not equivalent. ³√(x²) is the cube root of x², while (³√x)² is the square of the cube root of x. These expressions will generally yield different numerical values.
Q: How can I solve an equation involving ³√(x²)?
A: The approach depends on the equation's complexity. Often, you would need to isolate the ³√(x²) term, then cube both sides to eliminate the cube root, leaving you with an equation involving x². Finally, solve for x.
Q: Are there any online calculators or tools available to compute ³√(x²)?
A: While dedicated calculators specifically for ³√(x²) might be rare, any scientific calculator or mathematical software can handle this calculation using the cube root and squaring functions.
Conclusion: Mastering the Cube Root of x²
The cube root of x², while seemingly simple at first glance, reveals a rich tapestry of mathematical properties and applications. From its foundational definition to its use in various fields, understanding this concept is crucial for anyone seeking a strong foundation in mathematics and its applications. This guide has provided a comprehensive overview, covering the calculation methods, properties, real-world applications, and advanced concepts related to ³√(x²). By mastering this seemingly simple concept, you'll gain valuable insights that will enhance your problem-solving skills and deepen your mathematical understanding. Remember that consistent practice and exploration are key to fully grasping the nuances and power of this fundamental mathematical expression.
Latest Posts
Latest Posts
-
Lcm Of 18 And 7
Sep 19, 2025
-
What Time Is 14 45
Sep 19, 2025
-
Square Inches To Sq Ft
Sep 19, 2025
-
5 12 Simplified As A Fraction
Sep 19, 2025
-
What Is 8 6 Simplified
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Cube Root Of X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.