Factor 2x 2 1x 1
saludintensiva
Sep 22, 2025 · 7 min read
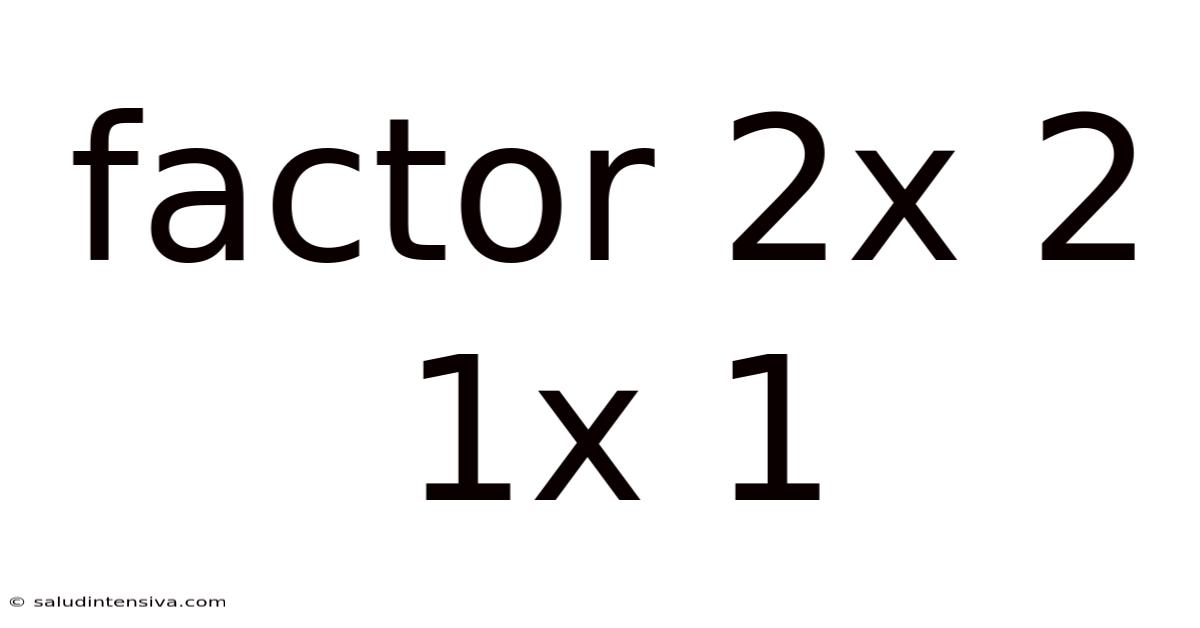
Table of Contents
Decoding the Enigma: A Deep Dive into Factorization of 2x² + 2x + 1
Many students encounter quadratic equations like 2x² + 2x + 1 and struggle with factorization. This seemingly simple expression hides a deeper mathematical concept that goes beyond simple factoring techniques often taught in introductory algebra. This comprehensive guide will explore the various methods to analyze this specific quadratic, delve into the underlying mathematical principles, and explain why it presents a unique challenge for straightforward factorization. We will uncover why some methods work and others fail, leading to a complete understanding of its properties and potential solutions.
Introduction: Understanding Quadratic Equations
Before tackling the specific equation 2x² + 2x + 1, let's establish a fundamental understanding of quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. The 'a', 'b', and 'c' are the coefficients of the equation. The solutions to this equation, often called roots or zeros, represent the values of x that satisfy the equation.
Finding the roots of a quadratic equation can be achieved through various methods, including factoring, completing the square, and using the quadratic formula. Factoring involves expressing the quadratic as a product of two linear expressions. This is the simplest method, but it's not always applicable. The quadratic formula, a more universal approach, always provides the solutions, regardless of whether the quadratic is factorable using simpler methods.
Attempting Traditional Factoring Techniques
Let's attempt to factor 2x² + 2x + 1 using traditional factoring methods. The standard approach involves finding two numbers that add up to the coefficient of the x term (b = 2) and multiply to the product of the coefficient of the x² term and the constant term (ac = 2 * 1 = 2). In this case, we're looking for two numbers that add up to 2 and multiply to 2. The only pairs of integers that multiply to 2 are (1, 2) and (-1, -2). Neither of these pairs adds up to 2.
This inability to find integer factors immediately suggests that the quadratic expression 2x² + 2x + 1 might not be factorable using simple integer coefficients. This doesn't mean it's not factorable at all, merely that the factors are more complex than expected.
The Quadratic Formula: A Universal Solution
When straightforward factoring fails, the quadratic formula provides a reliable method to find the roots of any quadratic equation. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Applying this formula to our equation (2x² + 2x + 1 = 0), where a = 2, b = 2, and c = 1, we get:
x = [-2 ± √(2² - 4 * 2 * 1)] / (2 * 2) x = [-2 ± √(4 - 8)] / 4 x = [-2 ± √(-4)] / 4 x = [-2 ± 2i] / 4 x = [-1 ± i] / 2
The solutions are x = (-1 + i)/2 and x = (-1 - i)/2. Notice the presence of 'i', the imaginary unit, where i² = -1. This confirms that the original quadratic expression 2x² + 2x + 1 is not factorable into real numbers. The roots are complex conjugates.
Understanding Complex Numbers and their Significance
The appearance of complex numbers in the solution highlights a crucial aspect of quadratic equations: not all quadratic equations have real number solutions. Complex numbers, numbers of the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, expand the number system beyond the real numbers. Complex numbers are essential in various fields, including electrical engineering, quantum mechanics, and signal processing.
The fact that 2x² + 2x + 1 has complex roots implies that its graph (a parabola) does not intersect the x-axis. The parabola lies entirely above the x-axis, indicating that there are no real values of x for which the expression equals zero.
Completing the Square: An Alternative Approach
Completing the square is another method to solve quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply this technique to 2x² + 2x + 1:
-
Divide by the coefficient of x²: x² + x + 1/2 = 0
-
Move the constant to the right side: x² + x = -1/2
-
Complete the square: To complete the square, take half of the coefficient of x (which is 1/2), square it (1/4), and add it to both sides:
x² + x + 1/4 = -1/2 + 1/4 x² + x + 1/4 = -1/4
-
Factor the perfect square trinomial: (x + 1/2)² = -1/4
-
Solve for x: Taking the square root of both sides:
x + 1/2 = ±√(-1/4) = ±i/2
x = -1/2 ± i/2
This method yields the same complex roots as the quadratic formula, confirming our previous findings.
Graphical Representation and Interpretation
Graphing the quadratic function y = 2x² + 2x + 1 provides a visual representation of its behavior. The parabola opens upwards (since the coefficient of x² is positive) and its vertex lies above the x-axis. The absence of x-intercepts visually confirms that there are no real roots. The graph illustrates the nature of the complex roots, showing that the equation has no solutions where the function's value is zero along the real number line.
Why Traditional Factoring Fails: Discriminant Analysis
The key to understanding why simple integer factoring fails lies in the discriminant of the quadratic equation. The discriminant, represented by Δ (delta), is the expression b² - 4ac found under the square root in the quadratic formula.
- If Δ > 0, the quadratic has two distinct real roots.
- If Δ = 0, the quadratic has one real root (a repeated root).
- If Δ < 0, the quadratic has two complex conjugate roots.
In our case, for 2x² + 2x + 1, the discriminant is:
Δ = 2² - 4 * 2 * 1 = 4 - 8 = -4
Since Δ < 0, the quadratic has two complex conjugate roots, explaining why traditional factoring techniques involving real integers fail.
Factorization with Complex Numbers: A More Advanced Perspective
While the quadratic doesn't factor nicely with real numbers, it can be factored using complex numbers. Recall the roots we found: x = (-1 + i)/2 and x = (-1 - i)/2. Using these roots, we can express the quadratic as:
2(x - [(-1 + i)/2])(x - [(-1 - i)/2]) = 0
This factorization involves complex numbers, illustrating that even seemingly simple quadratic equations can lead to more intricate mathematical structures.
Frequently Asked Questions (FAQ)
Q: Why is it important to understand complex numbers in algebra?
A: Complex numbers are fundamental in many advanced mathematical concepts and practical applications, including solving certain types of equations that don't have real number solutions, like the one discussed here.
Q: Can all quadratic equations be solved using the quadratic formula?
A: Yes, the quadratic formula provides a universal solution for any quadratic equation, regardless of whether it has real or complex roots.
Q: Is there a visual way to understand why this quadratic has complex roots?
A: Yes, graphing the quadratic function shows that the parabola doesn't intersect the x-axis, meaning there are no real values of x that make the function equal to zero.
Q: Are there any other methods to solve quadratic equations besides factoring, completing the square, and the quadratic formula?
A: While less common, numerical methods can be used to approximate the roots of quadratic equations, particularly when dealing with complex or irrational roots.
Conclusion: Expanding Mathematical Horizons
The exploration of the factorization of 2x² + 2x + 1 reveals that seemingly simple mathematical expressions can unveil deeper mathematical concepts and principles. The inability to factor this quadratic using traditional methods highlights the importance of understanding complex numbers and the limitations of simpler factoring techniques. Mastering methods like the quadratic formula and completing the square provides a robust toolkit for solving a wide range of quadratic equations, including those with complex solutions. The journey through this seemingly simple equation has broadened our understanding of the richness and complexity within the realm of algebra. It underscores that seemingly simple problems can open doors to more profound mathematical ideas and their practical applications.
Latest Posts
Latest Posts
-
Convert 55 Farenheit To Celsius
Sep 22, 2025
-
10 Deg Celsius To Fahrenheit
Sep 22, 2025
-
Rules For Writing Molecular Formulas
Sep 22, 2025
-
29 35 As A Percentage
Sep 22, 2025
-
Days Since June 4 2024
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 1x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.