Gcf Of 12 And 42
saludintensiva
Sep 09, 2025 · 6 min read
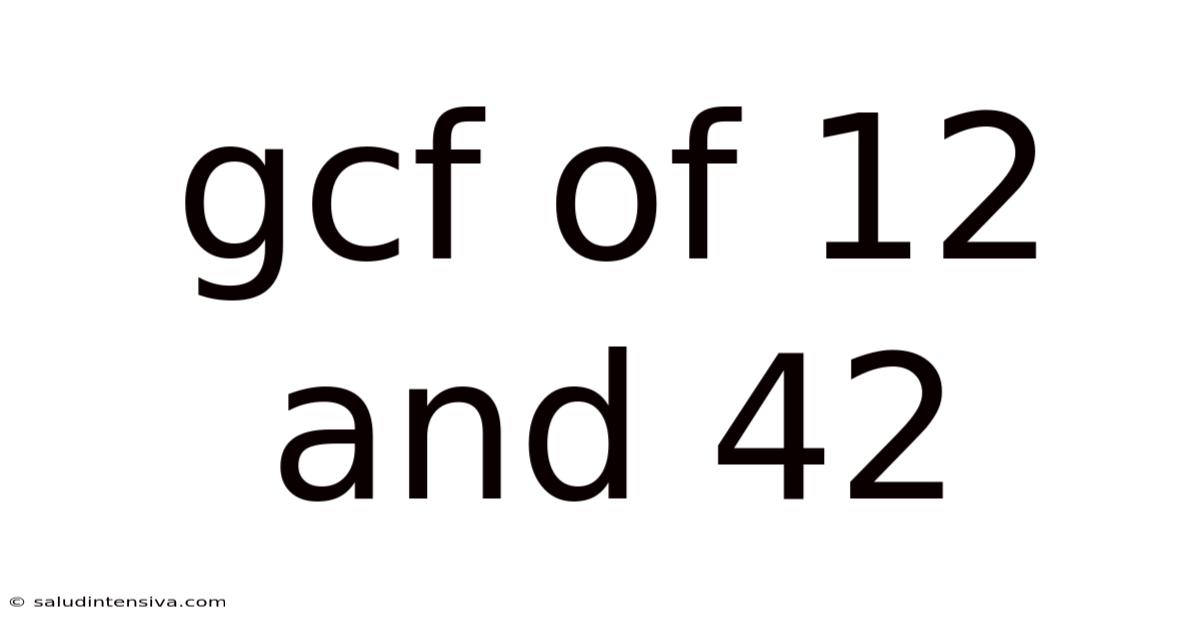
Table of Contents
Finding the Greatest Common Factor (GCF) of 12 and 42: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This seemingly simple task underpins more complex mathematical operations and is essential for simplifying fractions, solving algebraic equations, and understanding number theory. This article will explore various methods for determining the GCF of 12 and 42, providing a thorough understanding of the process and its underlying principles. We'll go beyond simply finding the answer and delve into the "why" behind the techniques, ensuring you grasp the core concepts.
Understanding Greatest Common Factors
Before we dive into calculating the GCF of 12 and 42, let's clarify what a GCF actually is. The GCF of two or more numbers is the largest number that divides evenly into all of the given numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of all the numbers in question. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42. The GCF will be the largest number present in both lists.
Method 1: Listing Factors
The most straightforward method, particularly for smaller numbers like 12 and 42, is to list all the factors of each number and then identify the largest common factor.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
By comparing the two lists, we can see that the common factors are 1, 2, 3, and 6. The largest of these common factors is 6. Therefore, the GCF of 12 and 42 is 6.
This method is simple and intuitive, making it ideal for teaching the concept to younger learners. However, it becomes less efficient as the numbers get larger, as listing all factors can be time-consuming and prone to errors.
Method 2: Prime Factorization
A more robust and efficient method, especially for larger numbers, involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let's find the prime factorization of 12 and 42:
-
12: We can start by dividing 12 by the smallest prime number, 2: 12 = 2 x 6. Then, we can further factor 6: 6 = 2 x 3. Therefore, the prime factorization of 12 is 2 x 2 x 3, or 2² x 3.
-
42: Again, we start with the smallest prime number, 2: 42 = 2 x 21. Next, we factor 21: 21 = 3 x 7. Therefore, the prime factorization of 42 is 2 x 3 x 7.
Now, to find the GCF, we identify the common prime factors and their lowest powers present in both factorizations. Both 12 and 42 have a 2 and a 3 as prime factors. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
This method is significantly more efficient for larger numbers because it systematically breaks down the numbers into their fundamental building blocks. It's less prone to error and provides a clear and logical pathway to the solution.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially useful when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 12 and 42:
- Start with the larger number (42) and the smaller number (12).
- Divide the larger number by the smaller number and find the remainder: 42 ÷ 12 = 3 with a remainder of 6.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (6).
- Repeat the division: 12 ÷ 6 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 6.
Therefore, the GCF of 12 and 42 using the Euclidean algorithm is 6.
This algorithm is incredibly efficient because it reduces the size of the numbers involved in each step, quickly converging on the GCF. It's particularly advantageous for finding the GCF of very large numbers where listing factors or prime factorization would be impractical.
Understanding the Significance of the GCF
The GCF isn't just a mathematical curiosity; it has practical applications in various areas:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 42/12 can be simplified by dividing both the numerator and the denominator by their GCF, which is 6: 42/12 = (42÷6) / (12÷6) = 7/2.
-
Solving Algebraic Equations: The GCF can help in factoring algebraic expressions, simplifying equations, and finding solutions.
-
Geometry and Measurement: The GCF is used in problems related to finding the greatest common measure of lengths, areas, or volumes. For example, finding the largest square tile that can perfectly cover a rectangular floor.
-
Number Theory: The GCF is a fundamental concept in number theory, playing a crucial role in various theorems and proofs.
Extending the Concept: More than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 12, 42, and 18:
-
Prime Factorization:
- 12 = 2² x 3
- 42 = 2 x 3 x 7
- 18 = 2 x 3² The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
-
Euclidean Algorithm (modified): The Euclidean algorithm can be extended by repeatedly finding the GCF of two numbers at a time. First, find the GCF of 12 and 42 (which is 6). Then, find the GCF of 6 and 18 (which is 6). Therefore, the GCF of 12, 42, and 18 is 6.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Is there a limit to how large the numbers can be for these methods?
- A: While listing factors becomes impractical for very large numbers, prime factorization and the Euclidean algorithm can be applied to numbers of any size, although computational power may become a limiting factor for extremely large numbers.
-
Q: Can I use a calculator to find the GCF?
- A: Many calculators and computer software programs have built-in functions to calculate the GCF.
Conclusion
Finding the greatest common factor is a valuable skill with applications across various mathematical disciplines. We've explored three different methods – listing factors, prime factorization, and the Euclidean algorithm – each with its strengths and weaknesses. Understanding these methods equips you with the tools to tackle GCF problems efficiently, regardless of the size of the numbers involved. Remember to choose the method best suited to the numbers you're working with, prioritizing efficiency and accuracy. Mastering the GCF lays a solid foundation for further exploration of mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
11 40 As A Decimal
Sep 09, 2025
-
Ai Lottery Number Generator Free
Sep 09, 2025
-
5 6 As A Percent
Sep 09, 2025
-
Fractions Equivalent To 5 10
Sep 09, 2025
-
How Long Is 111 Minutes
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.