Gcf Of 20 And 32
saludintensiva
Sep 13, 2025 · 6 min read
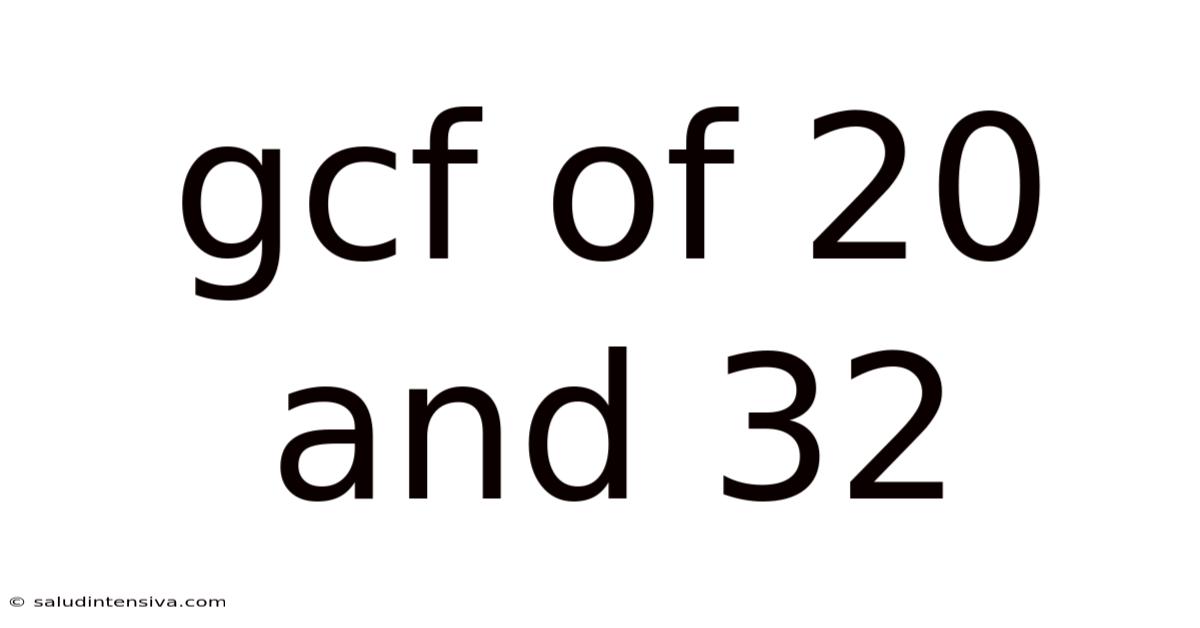
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 20 and 32: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with practical applications across various fields, from simplifying fractions to solving complex algebraic equations. This article will explore the GCF of 20 and 32, explaining multiple methods to calculate it, delving into the underlying mathematical principles, and providing examples to solidify understanding. We'll also touch upon the broader context of GCFs and their significance in mathematics.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 perfectly.
Methods to Find the GCF of 20 and 32
Several methods can be used to determine the GCF of 20 and 32. Let's explore the most common ones:
1. Listing Factors Method:
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 20: 1, 2, 4, 5, 10, 20
- Factors of 32: 1, 2, 4, 8, 16, 32
By comparing the lists, we see that the common factors are 1, 2, and 4. The largest among these is 4. Therefore, the GCF of 20 and 32 is 4.
This method is straightforward for smaller numbers but becomes less efficient as the numbers get larger.
2. Prime Factorization Method:
This method uses the prime factorization of each number to find the GCF. Prime factorization involves expressing a number as a product of its prime factors.
- Prime factorization of 20: 2 x 2 x 5 = 2² x 5
- Prime factorization of 32: 2 x 2 x 2 x 2 x 2 = 2⁵
To find the GCF, we identify the common prime factors and take the lowest power of each. In this case, the only common prime factor is 2, and the lowest power is 2². Therefore, the GCF of 20 and 32 is 2² = 4.
This method is more efficient than listing factors, especially for larger numbers. It provides a systematic approach to finding the GCF.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 20 and 32:
- Divide the larger number (32) by the smaller number (20): 32 ÷ 20 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (20) and the smaller number with the remainder (12): 20 ÷ 12 = 1 with a remainder of 8.
- Repeat the process: 12 ÷ 8 = 1 with a remainder of 4.
- Repeat again: 8 ÷ 4 = 2 with a remainder of 0.
Since the last non-zero remainder is 4, the GCF of 20 and 32 is 4.
The Euclidean algorithm is highly efficient and is often used in computer programs to calculate GCFs for very large numbers.
Beyond the GCF of 20 and 32: Applications and Extensions
The concept of the greatest common factor extends far beyond simply finding the largest number that divides two integers. It has numerous applications in various areas of mathematics and beyond:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 20/32 can be simplified by dividing both the numerator and denominator by their GCF, which is 4. This simplifies the fraction to 5/8.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a vital role in determining the solvability of certain types of Diophantine equations.
-
Modular Arithmetic: In modular arithmetic, which is used in cryptography and computer science, the GCF is essential for determining the existence and properties of modular inverses.
-
Least Common Multiple (LCM): The least common multiple (LCM) of two numbers is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related by the formula: LCM(a, b) = (a x b) / GCF(a, b). Finding the LCM is important in various applications, such as scheduling and finding common denominators.
-
Abstract Algebra: The concept of GCF extends to more abstract algebraic structures, such as rings and ideals, where the notion of greatest common divisor is generalized.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means that the numbers are relatively prime or coprime. This signifies that they share no common factors other than 1. For example, the GCF of 15 and 28 is 1.
Q: Can the GCF of two numbers be larger than either number?
A: No. The GCF of two numbers is always less than or equal to the smaller of the two numbers.
Q: Are there any shortcuts for finding the GCF of very large numbers?
A: For extremely large numbers, advanced algorithms such as the extended Euclidean algorithm and the binary GCD algorithm are employed. These algorithms offer significant improvements in computational efficiency.
Q: Why is the prime factorization method efficient?
A: The prime factorization method is efficient because prime numbers are the building blocks of all integers. By breaking down the numbers into their prime factors, we systematically identify the common components, which directly lead to the GCF.
Q: What are some real-world applications of GCF besides simplifying fractions?
A: Beyond simplifying fractions, GCF finds use in tasks like dividing objects into equal groups, scheduling events with overlapping cycles (finding the earliest time when two cyclical events coincide), and in computer science for tasks related to data compression and encryption.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with practical applications in various fields. We have explored three methods – listing factors, prime factorization, and the Euclidean algorithm – for calculating the GCF of 20 and 32, and we found that the GCF is 4. Understanding these methods and the underlying principles of number theory allows us to solve problems efficiently and appreciate the beauty and utility of this mathematical concept. The ability to find the GCF extends beyond basic arithmetic; it's a key stepping stone to more advanced mathematical concepts and problem-solving. Mastering GCF calculations equips you with a powerful tool for tackling complex mathematical challenges.
Latest Posts
Latest Posts
-
Gcf Of 18 And 14
Sep 13, 2025
-
How To Simplify 4 2
Sep 13, 2025
-
G Cm3 To G Ml
Sep 13, 2025
-
1600 Hours In Military Time
Sep 13, 2025
-
List Of Multiples Of 7
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 20 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.