Gcf Of 24 And 6
saludintensiva
Sep 17, 2025 · 6 min read
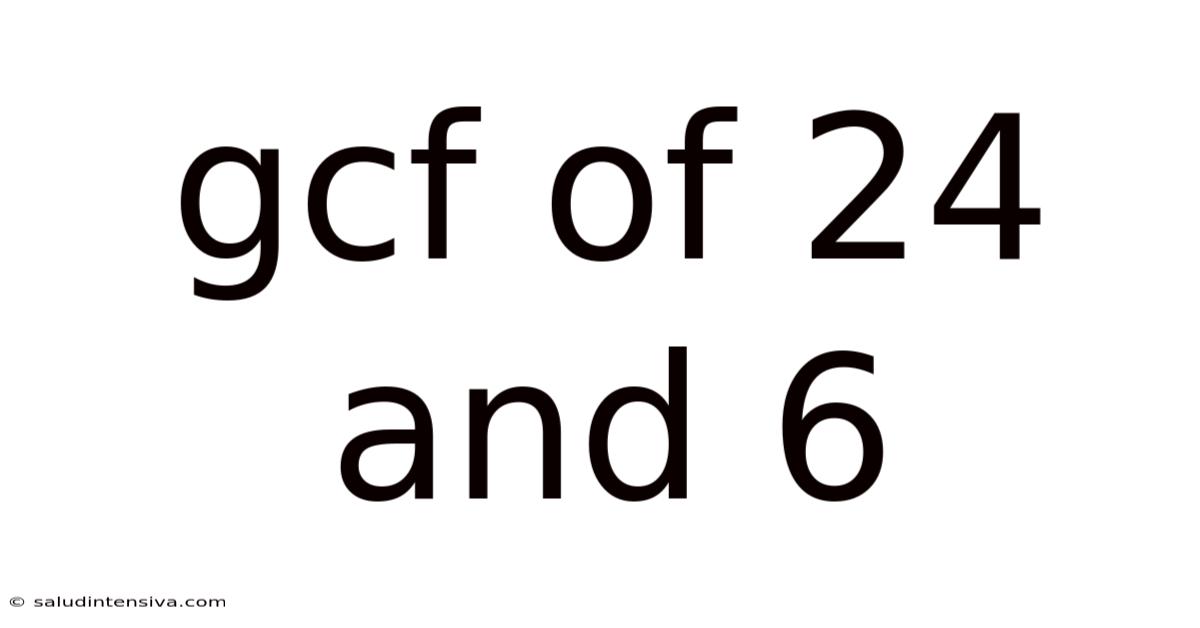
Table of Contents
Finding the Greatest Common Factor (GCF) of 24 and 6: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and many other mathematical operations. This article will comprehensively explain how to find the GCF of 24 and 6, exploring various methods and delving into the underlying mathematical principles. We'll also address frequently asked questions and provide examples to solidify your understanding. By the end, you'll not only know the GCF of 24 and 6 but also possess a solid grasp of this important mathematical concept.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6; therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is a straightforward method, particularly useful for smaller numbers like 24 and 6.
-
List the factors of each number:
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 6: 1, 2, 3, 6
-
Identify the common factors: The numbers that appear in both lists are 1, 2, 3, and 6.
-
Determine the greatest common factor: The largest number among the common factors is 6.
Therefore, the GCF of 24 and 6 is 6.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works well for larger numbers and provides a deeper understanding of the mathematical principles involved. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Find the prime factorization of each number:
- Prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 6: 6 = 2 x 3
-
Identify common prime factors: Both 24 and 6 share a prime factor of 2 and a prime factor of 3.
-
Multiply the common prime factors: Multiply the common prime factors together: 2 x 3 = 6.
Therefore, the GCF of 24 and 6 is 6. This method clearly shows why 6 is the GCF; it's the product of all the prime factors that both numbers share.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
-
Start with the larger number (24) and the smaller number (6):
-
Repeatedly subtract the smaller number from the larger number:
- 24 - 6 = 18
- 18 - 6 = 12
- 12 - 6 = 6
- 6 - 6 = 0
-
The last non-zero number is the GCF: The last non-zero result before reaching 0 is 6.
Therefore, the GCF of 24 and 6 is 6. While effective, this method can be tedious for very large numbers. A more efficient variant of the Euclidean algorithm uses division instead of subtraction, making it significantly faster for larger numbers. This involves dividing the larger number by the smaller number and taking the remainder. The process is repeated using the previous divisor and the remainder until the remainder is 0. The last non-zero divisor is the GCF. Let's illustrate:
- Divide 24 by 6: 24 ÷ 6 = 4 with a remainder of 0.
Since the remainder is 0, the GCF is the divisor, which is 6.
Mathematical Explanation: Why These Methods Work
The success of these methods hinges on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Prime factorization directly utilizes this theorem. The Euclidean algorithm, while seemingly different, also relies implicitly on this unique factorization. The repeated subtraction or division systematically removes common factors until only the greatest common factor remains. The listing factors method, while simpler, also inherently reflects the underlying principle of shared prime factors.
Applications of GCF
Understanding GCF has numerous applications in various mathematical fields and real-world scenarios:
-
Simplifying fractions: Finding the GCF of the numerator and denominator allows you to reduce a fraction to its simplest form. For example, the fraction 24/6 can be simplified to 4/1 (or simply 4) by dividing both the numerator and denominator by their GCF, which is 6.
-
Solving algebraic equations: GCF is crucial in factoring expressions, which is a fundamental technique in solving many algebraic equations.
-
Geometry problems: GCF is used in problems involving finding the greatest possible dimensions of squares or other shapes that can be formed from given lengths.
-
Real-world applications: GCF can be applied in scenarios involving dividing items into equal groups, determining the largest size of identical packages that can be created from a given quantity of items, or solving problems related to tiling or arranging objects in a grid.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they have no common factors other than 1.
Q: Can the GCF of two numbers be greater than either of the numbers?
A: No. The GCF is always less than or equal to the smaller of the two numbers.
Q: Which method is best for finding the GCF?
A: The best method depends on the numbers involved. For small numbers, listing factors is quick and easy. For larger numbers, prime factorization or the Euclidean algorithm (especially the division variant) are more efficient.
Q: Can I find the GCF of more than two numbers?
A: Yes, you can extend these methods to find the GCF of more than two numbers. For example, to find the GCF of 24, 6, and 18, you would find the prime factorization of each number and then identify the common prime factors that appear in all three factorizations.
Conclusion
Finding the greatest common factor is a valuable skill with widespread applications in mathematics and beyond. This article has explored three different methods for calculating the GCF, providing a step-by-step guide and mathematical explanations to enhance your understanding. Whether you use the method of listing factors, prime factorization, or the Euclidean algorithm, the result will always be the same – in this case, the GCF of 24 and 6 is 6. Remember to choose the method that best suits your needs and the complexity of the numbers involved. Mastering this concept will undoubtedly strengthen your mathematical foundation and problem-solving abilities. The ability to quickly and efficiently determine the GCF will prove invaluable as you progress in your mathematical studies.
Latest Posts
Latest Posts
-
Convert 240 Kg To Pounds
Sep 17, 2025
-
Gcf Of 42 And 35
Sep 17, 2025
-
21 Is 75 Of What
Sep 17, 2025
-
Gcf Of 3 And 8
Sep 17, 2025
-
90 Days From 10 23
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 24 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.