Gcf Of 26 And 39
saludintensiva
Sep 24, 2025 · 6 min read
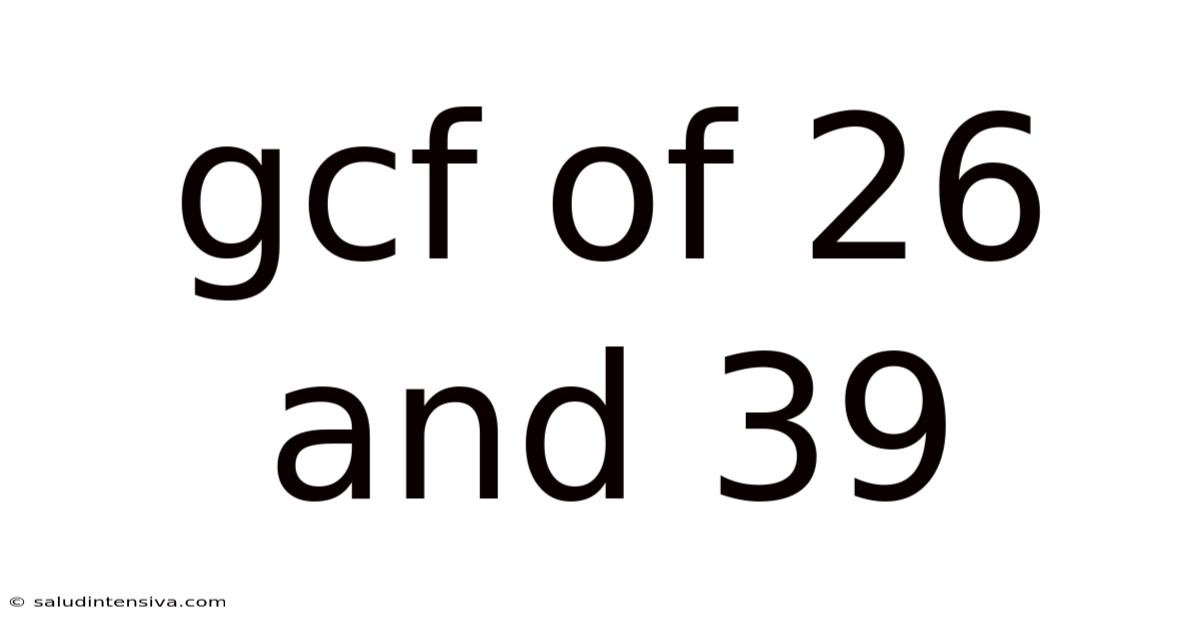
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 26 and 39: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles behind GCF calculations opens doors to more advanced concepts in number theory and algebra. This article will delve into the methods of finding the GCF of 26 and 39, explaining not just the how, but also the why, ensuring a comprehensive understanding for learners of all levels. We'll explore various approaches, from basic factorization to the powerful Euclidean algorithm, and address frequently asked questions along the way.
Understanding the Greatest Common Factor (GCF)
Before we tackle the specific case of 26 and 39, let's establish a firm understanding of what the GCF represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. Understanding this concept is crucial for simplifying fractions, solving algebraic equations, and even in advanced mathematical fields like cryptography.
Method 1: Prime Factorization
The first and most intuitive method for finding the GCF is through prime factorization. This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Let's start by finding the prime factorization of 26:
26 = 2 x 13
Both 2 and 13 are prime numbers. Now, let's do the same for 39:
39 = 3 x 13
Again, we have only prime numbers. Now, to find the GCF, we identify the common prime factors and multiply them together. In this case, both 26 and 39 share the prime factor 13. Therefore:
GCF(26, 39) = 13
This method is straightforward and easily understood, especially for smaller numbers. However, for larger numbers, finding the prime factorization can become quite time-consuming.
Method 2: Listing Factors
Another approach, particularly helpful for smaller numbers, involves listing all the factors of each number and then identifying the largest common factor.
Factors of 26: 1, 2, 13, 26 Factors of 39: 1, 3, 13, 39
By comparing the two lists, we can see that the common factors are 1 and 13. The largest of these common factors is 13. Therefore:
GCF(26, 39) = 13
This method is simple and visual, making it a good starting point for beginners. However, like prime factorization, it becomes less efficient with larger numbers.
Method 3: The Euclidean Algorithm
For larger numbers, the Euclidean algorithm provides a significantly more efficient method for finding the GCF. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 26 and 39:
- Step 1: Subtract the smaller number (26) from the larger number (39): 39 - 26 = 13
- Step 2: Now we have the numbers 26 and 13. Subtract the smaller number (13) from the larger number (26): 26 - 13 = 13
- Step 3: We now have the numbers 13 and 13. Since the numbers are equal, the GCF is 13.
Therefore, using the Euclidean algorithm:
GCF(26, 39) = 13
The Euclidean algorithm's efficiency stems from its iterative nature, avoiding the need for complete factorization. It's a powerful tool for finding the GCF of even very large numbers.
Understanding the Mathematical Basis: The Division Algorithm
The Euclidean algorithm implicitly relies on the division algorithm. The division algorithm states that for any integers a and b (where b is not zero), there exist unique integers q and r such that:
a = bq + r, where 0 ≤ r < |b|
Here, a is the dividend, b is the divisor, q is the quotient, and r is the remainder. The Euclidean algorithm repeatedly applies the division algorithm, using the remainder from each division as the new divisor in the next step, until the remainder is 0. The last non-zero remainder is the GCF.
Let's illustrate this with 26 and 39:
- 39 = 26 x 1 + 13 (Remainder is 13)
- 26 = 13 x 2 + 0 (Remainder is 0)
Since the remainder is 0, the last non-zero remainder (13) is the GCF.
Applications of GCF: Beyond Simple Arithmetic
The seemingly simple concept of the GCF finds numerous applications in various fields:
-
Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For example, the fraction 26/39 can be simplified to 2/3 by dividing both the numerator and the denominator by their GCF (13).
-
Solving Diophantine Equations: GCF plays a crucial role in determining the solvability of Diophantine equations, which are algebraic equations where only integer solutions are sought.
-
Modular Arithmetic: GCF is fundamental to modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Least Common Multiple (LCM): The GCF is closely related to the least common multiple (LCM). The product of the GCF and LCM of two numbers is equal to the product of the two numbers. This relationship provides a shortcut for calculating the LCM once the GCF is known.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can the Euclidean algorithm be used for more than two numbers?
A: Yes, the Euclidean algorithm can be extended to find the GCF of more than two numbers. You can find the GCF of the first two numbers, then find the GCF of that result and the third number, and so on.
-
Q: Are there any limitations to the prime factorization method?
A: While conceptually simple, the prime factorization method becomes computationally intensive for very large numbers. Finding the prime factors of extremely large numbers is a computationally hard problem, forming the basis of some modern cryptographic systems.
-
Q: Why is the Euclidean algorithm more efficient than prime factorization for large numbers?
A: The Euclidean algorithm avoids the need to completely factor the numbers. Its iterative process directly targets the GCF without needing to identify all prime factors. This makes it significantly faster for large numbers.
Conclusion
Finding the greatest common factor of 26 and 39, as demonstrated through various methods, highlights the importance of understanding fundamental number theory concepts. While prime factorization and listing factors are useful for smaller numbers, the Euclidean algorithm emerges as a powerful and efficient tool for handling larger numbers. Beyond its immediate application in simplifying fractions, the GCF plays a vital role in more advanced mathematical fields, showcasing the interconnectedness of mathematical concepts and the enduring relevance of seemingly basic arithmetic operations. Understanding the underlying principles behind GCF calculations not only enhances your mathematical skills but also provides a foundation for tackling more complex problems in various disciplines.
Latest Posts
Latest Posts
-
What Is Half Of 100
Sep 24, 2025
-
People Born In May 11
Sep 24, 2025
-
Make Money On Feet Finder
Sep 24, 2025
-
Convert 25 Cm To Inches
Sep 24, 2025
-
How Long Is 1 8 Hours
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 26 And 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.