Gcf Of 4 And 20
saludintensiva
Sep 16, 2025 · 6 min read
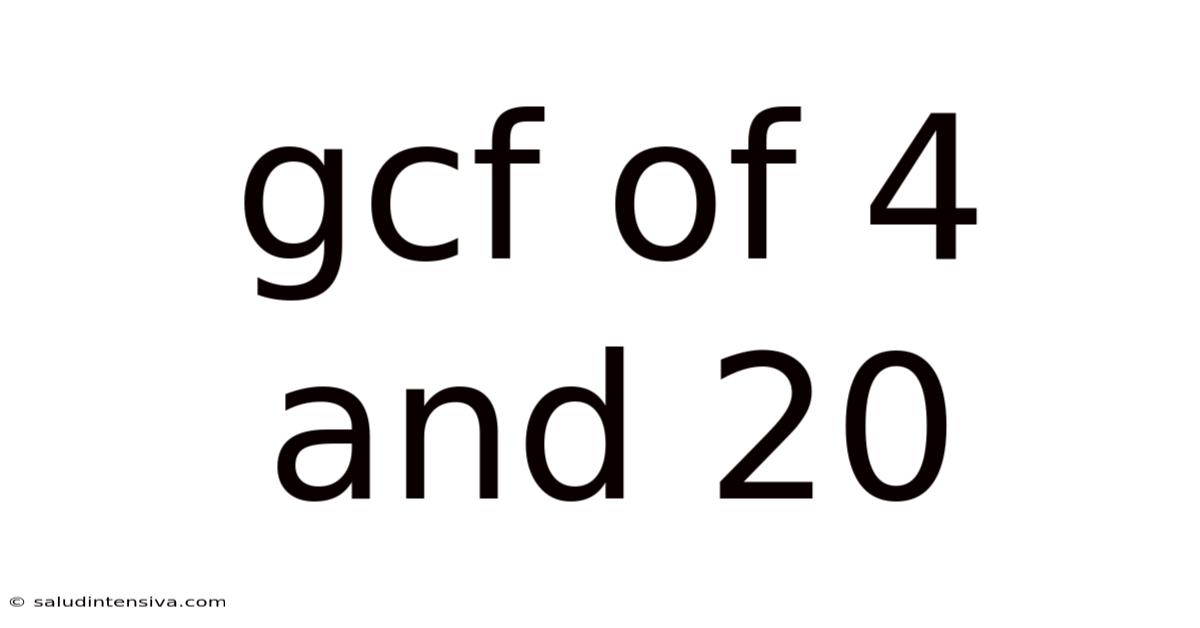
Table of Contents
Unveiling the Greatest Common Factor: A Deep Dive into GCF(4, 20)
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its applications in various fields. This comprehensive guide will explore the GCF of 4 and 20, not just by providing the answer, but by explaining multiple methods, delving into the theoretical background, and demonstrating its practical significance. We'll also address frequently asked questions and provide further examples to solidify your understanding.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For example, finding the GCF(4, 20) means identifying the largest number that divides both 4 and 20 evenly. This concept is fundamental in simplifying fractions, solving algebraic equations, and understanding number relationships.
Method 1: Prime Factorization
This is arguably the most robust and insightful method for finding the GCF. It involves breaking down each number into its prime factors – the prime numbers that multiply to give the original number.
- Step 1: Prime Factorization of 4: The prime factorization of 4 is 2 x 2, or 2².
- Step 2: Prime Factorization of 20: The prime factorization of 20 is 2 x 2 x 5, or 2² x 5.
- Step 3: Identifying Common Factors: Both 4 and 20 share two factors of 2.
- Step 4: Calculating the GCF: The GCF is the product of the common prime factors raised to the lowest power. In this case, it's 2² = 4.
Therefore, the GCF(4, 20) = 4. This method provides a clear visual representation of the shared factors, making it easier to understand why 4 is the greatest common factor.
Method 2: Listing Factors
This method is suitable for smaller numbers and provides a more intuitive approach for beginners.
- Step 1: List the Factors of 4: The factors of 4 are 1, 2, and 4.
- Step 2: List the Factors of 20: The factors of 20 are 1, 2, 4, 5, 10, and 20.
- Step 3: Identify Common Factors: The common factors of 4 and 20 are 1, 2, and 4.
- Step 4: Determine the Greatest Common Factor: The largest common factor is 4.
Therefore, the GCF(4, 20) = 4. This method is straightforward but can become cumbersome when dealing with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially larger ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
- Step 1: Divide the larger number (20) by the smaller number (4): 20 ÷ 4 = 5 with a remainder of 0.
- Step 2: Since the remainder is 0, the smaller number (4) is the GCF.
Therefore, the GCF(4, 20) = 4. This algorithm is computationally efficient and forms the basis for many advanced mathematical concepts.
Understanding the Significance of the GCF
The concept of the GCF extends far beyond simple arithmetic exercises. Its applications include:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For instance, the fraction 20/4 can be simplified to 5/1 (or simply 5) by dividing both the numerator and denominator by their GCF, which is 4.
-
Solving Algebraic Equations: GCF plays a crucial role in factoring algebraic expressions. For example, the expression 4x + 20 can be factored as 4(x + 5), where 4 is the GCF of 4 and 20.
-
Number Theory and Cryptography: GCF is fundamental to various concepts in number theory, including modular arithmetic and the Euclidean algorithm, which are used in modern cryptography to secure digital communications.
-
Geometry and Measurement: GCF is useful in solving problems involving lengths, areas, and volumes where finding common divisors is crucial. For example, if you need to cut a 4-meter long rope and a 20-meter long rope into pieces of equal length, the GCF (4) tells you the maximum length of each piece.
-
Real-World Applications: Consider scenarios like arranging items in equal rows or columns, dividing quantities into equal groups, or determining the largest possible size for identical squares within a rectangle.
Beyond 4 and 20: Exploring Further Examples
Let's examine how to find the GCF of other number pairs using the prime factorization method:
-
GCF(12, 18):
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
- Common factors: 2 and 3
- GCF(12, 18) = 2 x 3 = 6
-
GCF(24, 36):
- Prime factorization of 24: 2³ x 3
- Prime factorization of 36: 2² x 3²
- Common factors: 2² and 3
- GCF(24, 36) = 2² x 3 = 12
-
GCF(15, 25):
- Prime factorization of 15: 3 x 5
- Prime factorization of 25: 5²
- Common factors: 5
- GCF(15, 25) = 5
These examples demonstrate the versatility and power of the prime factorization method, providing a systematic way to find the GCF of any two integers.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can I use the Euclidean algorithm for numbers with decimals?
- A: The Euclidean algorithm is primarily designed for integers. For numbers with decimals, you would typically need to convert them to fractions and then apply the algorithm to the numerators and denominators.
-
Q: Is there a limit to the size of numbers for which I can find the GCF?
- A: Theoretically, there's no limit. However, the computational time for methods like prime factorization can increase significantly with very large numbers. The Euclidean algorithm remains efficient even for extremely large numbers.
-
Q: What if I have more than two numbers? How do I find the GCF?
- A: To find the GCF of more than two numbers, you can find the GCF of any two numbers first, then find the GCF of the result and the next number, and so on.
Conclusion: Mastering the GCF
Understanding the greatest common factor is a cornerstone of mathematical proficiency. This article has explored various methods for finding the GCF, highlighting their strengths and applications. From the straightforward listing of factors to the efficient Euclidean algorithm and the insightful prime factorization method, we've demonstrated different approaches to solve this fundamental mathematical problem. Mastering the concept of GCF not only enhances your arithmetic skills but also provides a foundation for understanding more advanced mathematical concepts and their real-world applications. Remember, the key is to choose the method that best suits the numbers involved and your level of understanding. Practice is key to solidifying your knowledge and building confidence in your ability to tackle more complex mathematical problems.
Latest Posts
Latest Posts
-
13 9 Degrees Celsius To Fahrenheit
Sep 16, 2025
-
How Long Is 103 Minutes
Sep 16, 2025
-
What Is Half Of 31
Sep 16, 2025
-
5 1 4 As A Percent
Sep 16, 2025
-
1330 Military Time To Normal
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 4 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.