Gcf Of 5 And 30
saludintensiva
Sep 11, 2025 · 7 min read
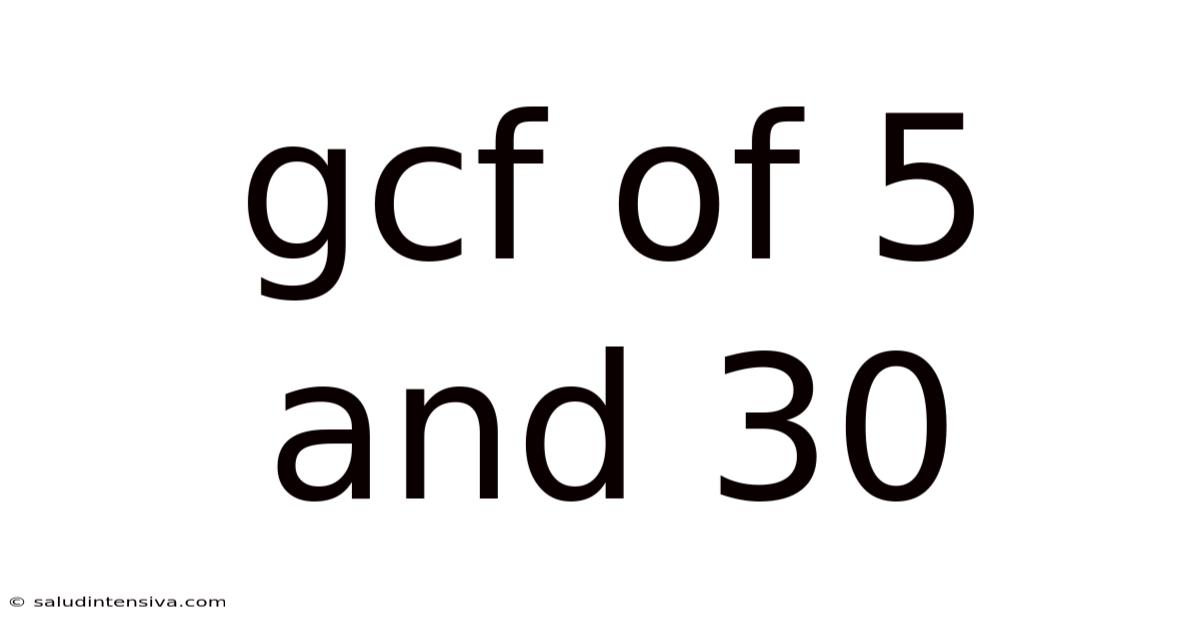
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 5 and 30: A Comprehensive Guide
Finding the greatest common factor (GCF) of two numbers might seem like a simple task, especially for seemingly straightforward pairs like 5 and 30. However, understanding the underlying principles behind GCF calculation is crucial for mastering more complex mathematical concepts. This comprehensive guide will not only show you how to find the GCF of 5 and 30 but also delve into the various methods, explaining the underlying mathematical reasoning and providing you with a solid foundation in number theory. We'll explore different approaches, from prime factorization to the Euclidean algorithm, ensuring you grasp the concept fully.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides exactly into two or more numbers without leaving a remainder. It's a fundamental concept in arithmetic and algebra, crucial for simplifying fractions, solving equations, and understanding number properties. Understanding GCF is essential for various mathematical applications, from simplifying algebraic expressions to solving Diophantine equations.
Method 1: Prime Factorization
The prime factorization method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this method to find the GCF of 5 and 30.
1. Find the prime factors of 5:
5 is a prime number itself, so its prime factorization is simply 5.
2. Find the prime factors of 30:
30 can be broken down as follows:
30 = 2 x 15 = 2 x 3 x 5
3. Identify common prime factors:
Comparing the prime factorizations of 5 and 30 (5 and 2 x 3 x 5), we see that the only common prime factor is 5.
4. Calculate the GCF:
The GCF is the product of the common prime factors. In this case, the only common prime factor is 5, so the GCF of 5 and 30 is 5.
This method is particularly useful for visualizing the relationship between the numbers and understanding their composition. It's an excellent approach for smaller numbers, providing a clear and intuitive understanding of the concept. However, for larger numbers, prime factorization can become computationally intensive.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
1. List the factors of 5:
The factors of 5 are 1 and 5.
2. List the factors of 30:
The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
3. Identify common factors:
Comparing the two lists, we find that the common factors are 1 and 5.
4. Determine the GCF:
The greatest of the common factors is 5. Therefore, the GCF of 5 and 30 is 5.
This method is straightforward for smaller numbers but becomes less efficient as the numbers increase in size. The process of listing all factors can be time-consuming and prone to errors for larger numbers.
Method 3: The Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where prime factorization becomes cumbersome. It relies on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to find the GCF of 5 and 30:
1. Divide the larger number (30) by the smaller number (5):
30 ÷ 5 = 6 with a remainder of 0.
2. Interpret the result:
Since the remainder is 0, the smaller number (5) is the GCF.
Therefore, the GCF of 5 and 30 is 5.
The Euclidean algorithm is remarkably efficient, even for very large numbers. Its iterative nature makes it computationally less demanding than prime factorization, particularly for numbers that are not easily factored. This algorithm forms the basis of many more advanced mathematical computations.
Mathematical Properties and Significance of GCF
The GCF possesses several crucial mathematical properties:
-
Commutative Property: The GCF of two numbers remains the same regardless of their order. GCF(a, b) = GCF(b, a)
-
Associative Property: This property allows us to find the GCF of multiple numbers sequentially. GCF(a, GCF(b, c)) = GCF(GCF(a, b), c)
-
Distributive Property with LCM: The product of the GCF and LCM (Least Common Multiple) of two numbers is equal to the product of the two numbers: GCF(a, b) * LCM(a, b) = a * b. This relationship is fundamental in simplifying fractions and solving various mathematical problems.
Understanding these properties is vital for applying GCF effectively in more complex mathematical scenarios.
Applications of GCF in Real-World Scenarios
The concept of GCF extends far beyond abstract mathematical exercises. It has practical applications in various real-world scenarios:
-
Simplifying Fractions: GCF is essential for reducing fractions to their simplest form. For example, the fraction 30/5 can be simplified to 6/1 (or simply 6) by dividing both the numerator and denominator by their GCF, which is 5.
-
Dividing Objects Equally: Imagine you have 30 apples and want to divide them equally among 5 friends. The GCF (5) tells you each friend will receive 6 apples.
-
Geometry and Measurement: GCF is utilized in finding the largest square tile that can perfectly cover a rectangular floor of given dimensions.
-
Music Theory: GCF plays a role in understanding musical intervals and harmonies.
-
Computer Science: GCF algorithms are employed in cryptography and computer graphics.
Beyond the Basics: Exploring Related Concepts
Understanding GCF opens doors to exploring related concepts in number theory:
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of two or more given numbers. GCF and LCM are inversely related, as mentioned earlier.
-
Coprime Numbers: Two numbers are coprime (or relatively prime) if their GCF is 1. Understanding coprime numbers is crucial in various areas of mathematics and computer science.
-
Modular Arithmetic: GCF plays a role in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus).
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are coprime (relatively prime) and have no common factors other than 1.
-
Q: Can the GCF of two numbers be greater than either of the numbers?
A: No. The GCF of two numbers will always be less than or equal to the smaller of the two numbers.
-
Q: Is there a limit to the size of numbers for which we can find the GCF?
A: While manual methods become tedious for very large numbers, computational algorithms can efficiently find the GCF of arbitrarily large numbers.
-
Q: What is the difference between the GCF and the LCM?
A: The GCF is the greatest common factor, while the LCM is the least common multiple. The GCF finds the largest number that divides both numbers evenly, while the LCM finds the smallest number that is a multiple of both numbers.
Conclusion
Finding the greatest common factor of 5 and 30, which is 5, might appear straightforward. However, this exploration has unveiled the deeper mathematical principles behind GCF calculation. We've examined three distinct methods—prime factorization, listing factors, and the Euclidean algorithm—each offering unique advantages depending on the context. Beyond the calculation itself, we've delved into the mathematical properties of GCF, its real-world applications, and related concepts in number theory. This comprehensive understanding equips you not just with the ability to find the GCF but also with a solid foundation for tackling more advanced mathematical challenges. Remember that the journey of mathematical understanding is continuous, and each concept learned builds upon the previous one, enriching your overall comprehension of the mathematical world.
Latest Posts
Latest Posts
-
Equivalent Fraction For 3 10
Sep 11, 2025
-
Round To The Nearest Year
Sep 11, 2025
-
Price Per Kg To Lb
Sep 11, 2025
-
Gcf Of Two Monomials Calculator
Sep 11, 2025
-
5 To The Power 4
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 5 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.