Gcf Of 7 And 28
saludintensiva
Sep 17, 2025 · 6 min read
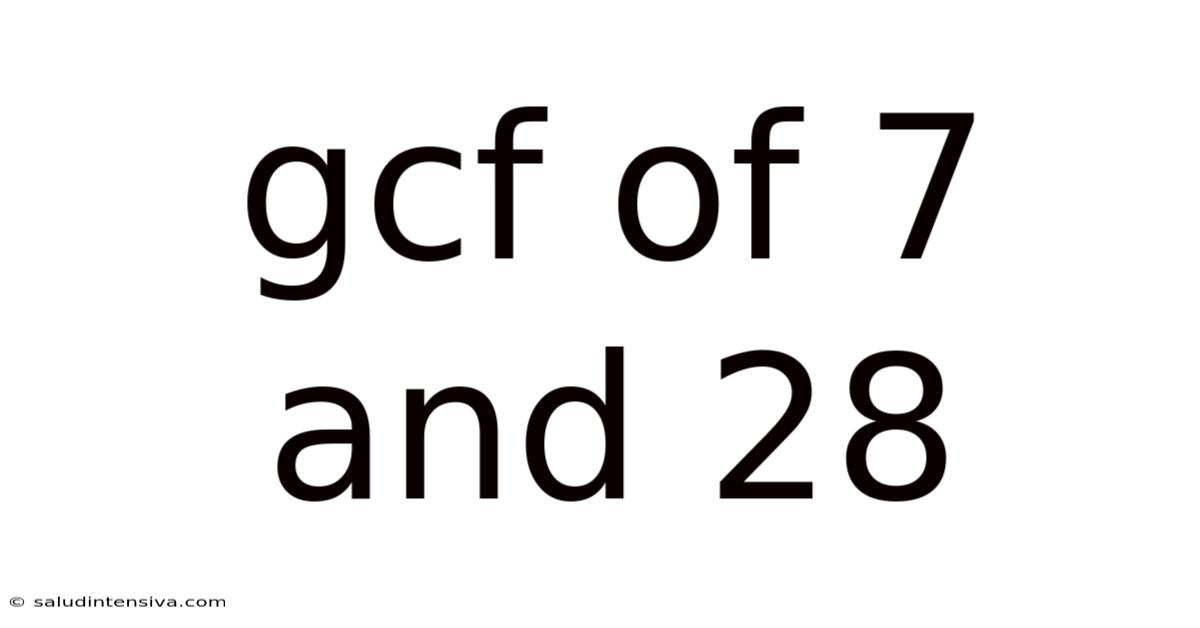
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 7 and 28: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles reveals a fascinating glimpse into number theory and its practical applications. This article will delve into the GCF of 7 and 28, not only providing the answer but also explaining the various methods for calculating it, exploring its significance, and addressing frequently asked questions. We will cover different approaches, suitable for various levels of mathematical understanding, ensuring you gain a comprehensive grasp of the concept.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific case of 7 and 28, let's establish a clear definition. The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding this basic concept is crucial for solving more complex problems in mathematics and other fields.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers like 7 and 28, involves listing all the factors of each number and then identifying the largest common factor.
Factors of 7: 1, 7
Factors of 28: 1, 2, 4, 7, 14, 28
By comparing the two lists, we can see that the common factors are 1 and 7. The largest of these common factors is 7. Therefore, the GCF of 7 and 28 is 7.
This method is easy to visualize and understand, making it ideal for introductory lessons on GCF. However, it becomes less practical when dealing with larger numbers, as listing all factors can be time-consuming and prone to errors.
Method 2: Prime Factorization
A more efficient and elegant method, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization of 7: 7 (7 is a prime number itself)
-
Prime Factorization of 28: 2 x 2 x 7 = 2² x 7
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. In this case, the only common prime factor is 7, and its lowest power is 7¹ (or simply 7). Therefore, the GCF of 7 and 28 is 7.
This method is more systematic and less prone to errors than listing factors, making it suitable for larger numbers and more advanced mathematical problems. The prime factorization method provides a deeper understanding of the number's structure and its relationship to other numbers.
Method 3: Euclidean Algorithm
For larger numbers, the Euclidean algorithm offers a significantly more efficient approach. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 7 and 28:
-
Start with the larger number (28) and the smaller number (7).
-
Subtract the smaller number from the larger number repeatedly: 28 - 7 = 21; 21 - 7 = 14; 14 - 7 = 7.
-
Continue subtracting until the remainder is smaller than the smaller number or equal. We reach 7.
-
Since the difference is now 7, which is the smaller number itself, the GCF is 7.
The Euclidean algorithm avoids the need for prime factorization and is computationally efficient for even very large numbers. This algorithm's elegance and efficiency make it a cornerstone of number theory and computer science.
Significance of the Greatest Common Factor
The concept of GCF extends far beyond simple arithmetic exercises. It has significant applications in various fields:
-
Simplification of Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For instance, the fraction 28/7 can be simplified to 4/1 (or simply 4) by dividing both the numerator and denominator by their GCF, which is 7.
-
Algebraic Expressions: GCF plays a crucial role in simplifying algebraic expressions. Factoring out the GCF from an expression helps in solving equations and simplifying complex calculations.
-
Geometry and Measurement: GCF is essential in solving geometrical problems involving lengths, areas, and volumes. For example, finding the largest square tile that can perfectly cover a rectangular floor requires calculating the GCF of the floor's length and width.
-
Cryptography: GCF is a fundamental concept in cryptography, particularly in RSA encryption, which relies on the difficulty of finding the GCF of very large numbers.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is a highly efficient algorithm used in various computer science applications, including cryptography and computer-aided design (CAD).
Further Exploration: GCF and Least Common Multiple (LCM)
The GCF is closely related to the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. There's a useful relationship between the GCF and LCM:
For any two positive integers a and b, the product of their GCF and LCM is equal to the product of the two numbers:
GCF(a, b) * LCM(a, b) = a * b
In our example:
GCF(7, 28) * LCM(7, 28) = 7 * 28
7 * 28 = 196
Therefore, LCM(7, 28) = 196 / 7 = 28. This relationship provides a shortcut for finding the LCM once the GCF is known.
Frequently Asked Questions (FAQ)
Q1: Is the GCF always smaller than the numbers involved?
A1: Yes, the GCF is always less than or equal to the smaller of the two numbers. It cannot be larger because the GCF must divide both numbers evenly.
Q2: What is the GCF of a number and itself?
A2: The GCF of a number and itself is the number itself. For example, GCF(7, 7) = 7.
Q3: What is the GCF of 0 and any other number?
A3: The GCF of 0 and any other number is the other number. This is because any number divides 0 evenly.
Q4: Can the GCF of two numbers be 1?
A4: Yes, if two numbers have no common factors other than 1, their GCF is 1. Such numbers are called relatively prime or coprime.
Conclusion
Finding the GCF of 7 and 28, which is 7, is not just a simple arithmetic calculation. It's a gateway to understanding fundamental concepts in number theory, revealing the elegance and efficiency of algorithms like the Euclidean algorithm. The GCF has practical applications in various fields, highlighting its importance beyond classroom exercises. Mastering the different methods for calculating the GCF provides a strong foundation for further exploration of mathematical concepts and problem-solving skills. We've explored multiple methods, from simple factor listing to the powerful Euclidean algorithm, providing you with the tools to tackle GCF problems effectively, regardless of the numbers' magnitude. The knowledge gained will prove invaluable in your future mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 200db Depreciation Method
Sep 17, 2025
-
4 To Power Of 8
Sep 17, 2025
-
Absolute Value Of 3 4
Sep 17, 2025
-
Half Of 3 3 4 Inches
Sep 17, 2025
-
How High Is 3 Meters
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 7 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.