Gcf Of 7 And 35
saludintensiva
Sep 17, 2025 · 6 min read
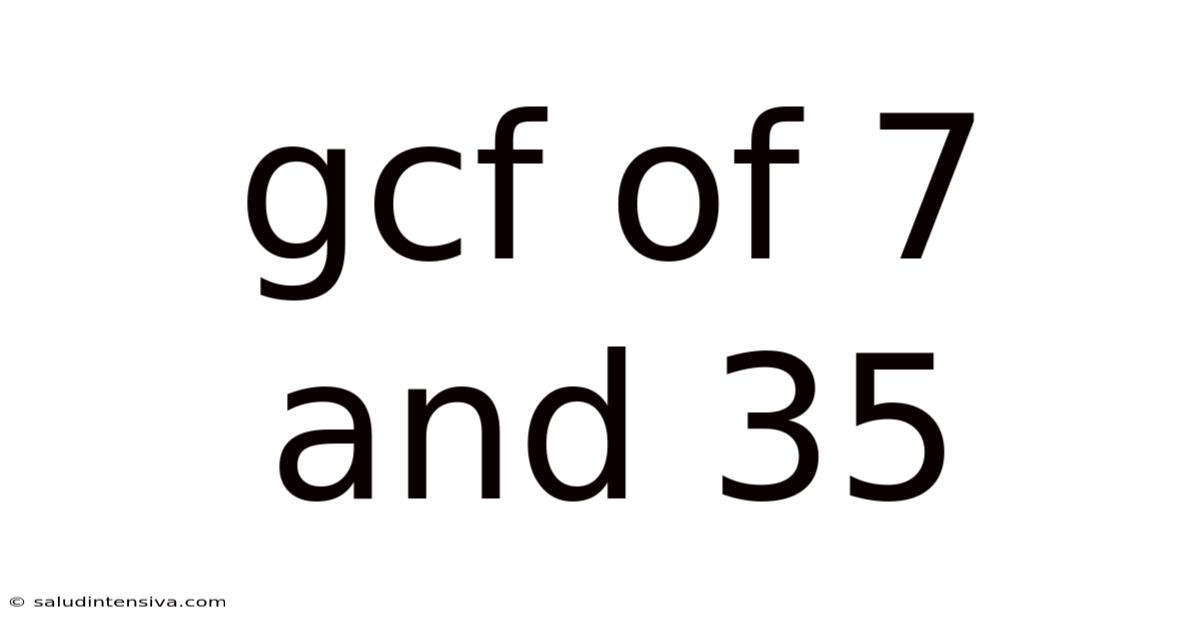
Table of Contents
Understanding the Greatest Common Factor (GCF) of 7 and 35: A Deep Dive
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, especially when dealing with small numbers like 7 and 35. However, understanding the underlying concepts and different methods for calculating the GCF is crucial for building a strong foundation in mathematics. This comprehensive guide will explore the GCF of 7 and 35, delve into various methods for finding the GCF, and explain the broader significance of this concept in mathematics and beyond. We'll also address frequently asked questions to ensure a complete understanding.
What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF), also known as the highest common factor (HCF) or greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without any remainder.
Finding the GCF of 7 and 35: Methods and Explanations
Let's explore several methods to find the GCF of 7 and 35. These methods are applicable to finding the GCF of any two numbers.
1. Listing Factors:
This is the most straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
- Factors of 7: 1, 7
- Factors of 35: 1, 5, 7, 35
The common factors are 1 and 7. Therefore, the GCF of 7 and 35 is 7.
2. Prime Factorization:
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Then, we identify the common prime factors and multiply them to find the GCF.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 35: 5 x 7
The only common prime factor is 7. Therefore, the GCF of 7 and 35 is 7.
3. Euclidean Algorithm:
The Euclidean algorithm is a more efficient method for finding the GCF of larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 7 and 35:
- Divide the larger number (35) by the smaller number (7): 35 ÷ 7 = 5 with a remainder of 0.
- Since the remainder is 0, the GCF is the divisor in the last step, which is 7.
This method is particularly advantageous when dealing with larger numbers where listing factors becomes cumbersome.
Understanding the Concept of Divisibility
The concept of divisibility is central to understanding GCF. A number is divisible by another number if it can be divided evenly (without a remainder). For example:
- 35 is divisible by 7 because 35 ÷ 7 = 5.
- 7 is divisible by 1 and 7.
- 35 is divisible by 1, 5, 7, and 35.
Understanding divisibility helps us quickly identify potential common factors. Knowing divisibility rules (e.g., a number is divisible by 2 if it's even, divisible by 3 if the sum of its digits is divisible by 3) can significantly speed up the process of finding the GCF.
The Significance of GCF in Mathematics and Beyond
The GCF is a fundamental concept in various areas of mathematics:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 35/7 can be simplified to 5/1 by dividing both the numerator and the denominator by their GCF (7).
-
Algebra: GCF is used to factor algebraic expressions. For example, the expression 7x + 35 can be factored as 7(x + 5), where 7 is the GCF of 7x and 35.
-
Number Theory: GCF plays a vital role in number theory, particularly in topics like modular arithmetic and Diophantine equations.
-
Real-World Applications: While not always explicitly stated, the GCF is implicitly used in various real-world situations:
-
Dividing items evenly: Imagine you have 35 apples and want to distribute them evenly among 7 friends. The GCF (7) tells you each friend will receive 5 apples.
-
Measurement and Construction: GCF can be used to find the largest possible square tiles to cover a rectangular area without cutting any tiles.
-
Project Management: When planning tasks that need to be completed in different amounts of time, understanding common factors can help optimize scheduling.
-
Expanding the Concept: GCF of More Than Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 7, 35, and 49:
-
Prime Factorization:
- 7 = 7
- 35 = 5 x 7
- 49 = 7 x 7
The common prime factor is 7. Therefore, the GCF of 7, 35, and 49 is 7.
-
Euclidean Algorithm (Extended): While the standard Euclidean algorithm works for two numbers, extensions exist for multiple numbers. However, these can become more complex. For multiple numbers, prime factorization is often a more efficient approach.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. This indicates that they share no common factors other than 1.
Q: Is there a limit to the size of numbers for which we can find the GCF?
A: No. The methods described, especially the Euclidean algorithm, can be applied to numbers of any size, although very large numbers might require computational assistance.
Q: How does the GCF relate to the Least Common Multiple (LCM)?
A: The GCF and LCM are closely related. For any two numbers a and b, the product of their GCF and LCM is equal to the product of the two numbers: GCF(a, b) x LCM(a, b) = a x b. This relationship provides a way to find the LCM if the GCF is known, and vice versa.
Q: Why is learning about GCF important?
A: Understanding GCF is foundational for many areas of mathematics and problem-solving. It helps develop critical thinking skills, enhances algebraic manipulation, and allows for a deeper understanding of number properties. Its applications extend beyond the classroom into various practical scenarios.
Conclusion
Finding the greatest common factor (GCF) of 7 and 35, as demonstrated through various methods, is more than a simple arithmetic exercise. It underscores fundamental mathematical concepts like divisibility, prime factorization, and the Euclidean algorithm. Mastering these concepts and understanding the broader significance of the GCF lays a strong foundation for further mathematical explorations and problem-solving abilities across diverse fields. The seemingly simple task of determining the GCF of 7 and 35 serves as a gateway to a deeper understanding of the intricacies of number theory and its real-world implications.
Latest Posts
Latest Posts
-
Volume Of Truncated Cone Calculator
Sep 17, 2025
-
What Are Multiples Of 100
Sep 17, 2025
-
37 20 As A Decimal
Sep 17, 2025
-
200 Percent In Decimal Form
Sep 17, 2025
-
17 3 As A Mixed Number
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 7 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.