Gcf Of 8 And 32
saludintensiva
Sep 12, 2025 · 6 min read
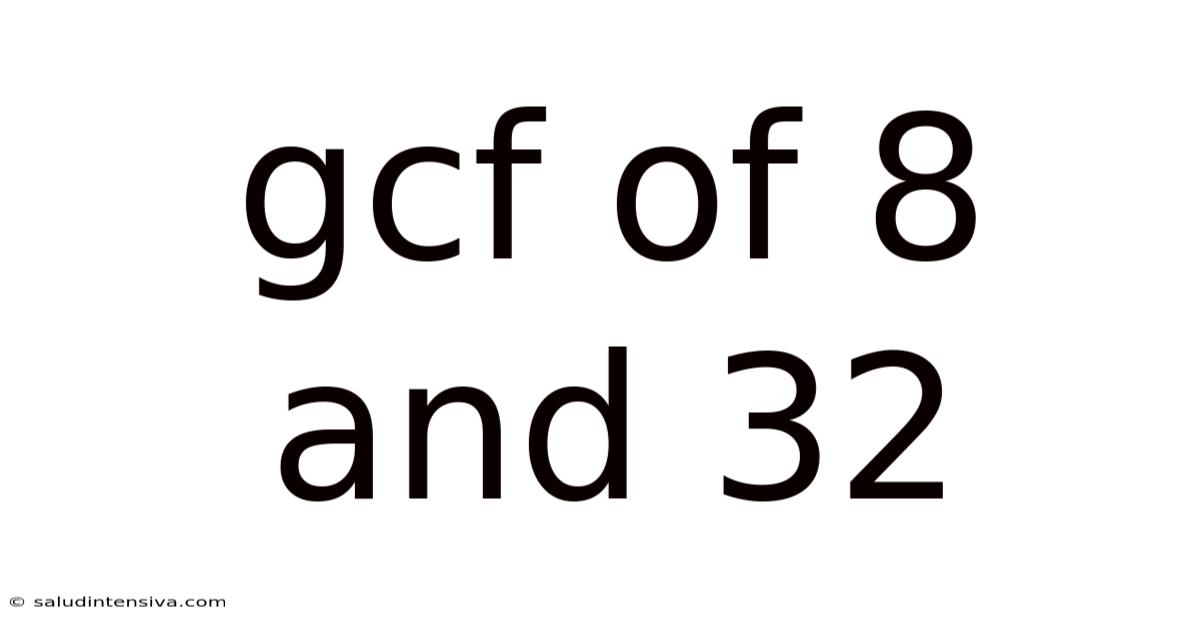
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 8 and 32: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for calculating the GCF unlocks a deeper appreciation of number theory and its applications in various fields like cryptography and computer science. This article will thoroughly explore how to find the GCF of 8 and 32, employing several methods and delving into the mathematical concepts behind them. We will also explore the broader implications of GCF and its relevance beyond simple calculations.
Understanding the Greatest Common Factor (GCF)
Before we jump into the specifics of finding the GCF of 8 and 32, let's solidify our understanding of what a GCF actually is. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
This concept is fundamental in simplifying fractions, solving algebraic equations, and even in more advanced mathematical applications. Understanding the GCF allows us to reduce fractions to their simplest form and to solve problems involving ratios and proportions efficiently.
Method 1: Listing Factors
The most straightforward method for finding the GCF of small numbers like 8 and 32 is by listing all the factors of each number and then identifying the largest common factor.
Factors of 8: 1, 2, 4, 8
Factors of 32: 1, 2, 4, 8, 16, 32
By comparing the two lists, we can see that the common factors are 1, 2, 4, and 8. The largest of these common factors is 8. Therefore, the GCF of 8 and 32 is 8.
Method 2: Prime Factorization
Prime factorization is a more systematic and powerful method for finding the GCF, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 8:
8 = 2 x 2 x 2 = 2³
Prime Factorization of 32:
32 = 2 x 2 x 2 x 2 x 2 = 2⁵
Now, we identify the common prime factors and their lowest powers. Both 8 and 32 have only one prime factor: 2. The lowest power of 2 present in both factorizations is 2³. Therefore, the GCF of 8 and 32 is 2³ = 8. This method is particularly useful for finding the GCF of larger numbers where listing all factors becomes cumbersome.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 8 and 32:
- Start with the larger number (32) and the smaller number (8).
- Divide the larger number by the smaller number and find the remainder: 32 ÷ 8 = 4 with a remainder of 0.
- Since the remainder is 0, the GCF is the smaller number, which is 8.
Therefore, the GCF of 8 and 32 is 8. The Euclidean algorithm is remarkably efficient because it avoids the need for complete prime factorization, making it suitable for very large numbers where prime factorization becomes computationally expensive.
The Significance of the GCF beyond Simple Calculations
The GCF isn't just a theoretical concept; it has practical applications in various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 32/8 can be simplified to 4/1 (or simply 4) by dividing both the numerator and denominator by their GCF, which is 8.
-
Solving Problems Involving Ratios and Proportions: Understanding the GCF helps in simplifying ratios and proportions, making them easier to work with. For instance, if a recipe calls for a ratio of 8 cups of flour to 32 cups of water, we can simplify this ratio to 1:4 by dividing both quantities by their GCF (8).
-
Cryptography: The GCF plays a vital role in certain cryptographic algorithms, such as the RSA algorithm, which is widely used for secure communication and data encryption. The algorithm's security relies heavily on the difficulty of finding the GCF of two very large numbers.
-
Computer Science: The GCF is used in various computer science algorithms and data structures. It’s employed in finding the least common multiple (LCM), which is essential in tasks such as scheduling and resource allocation.
-
Geometry: The GCF can be applied in geometric problems related to finding the greatest common measure of lengths or areas.
Exploring the LCM (Least Common Multiple)
While this article focuses on the GCF, it’s important to briefly touch upon the closely related concept of the Least Common Multiple (LCM). The LCM of two integers is the smallest positive integer that is divisible by both integers.
For our example numbers, 8 and 32:
- Multiples of 8: 8, 16, 24, 32, 40, 48...
- Multiples of 32: 32, 64, 96...
The smallest common multiple of 8 and 32 is 32. Therefore, the LCM of 8 and 32 is 32.
The GCF and LCM are related by the following formula:
GCF(a, b) x LCM(a, b) = a x b
Let’s verify this for our example:
GCF(8, 32) x LCM(8, 32) = 8 x 32 = 256
8 x 32 = 256
The formula holds true. This relationship provides a useful method for calculating the LCM if the GCF is already known, or vice versa.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, the numbers are called relatively prime or coprime. This means they have no common factors other than 1.
Q2: Can the GCF of two numbers be larger than the smaller number?
A2: No. The GCF can never be larger than the smaller of the two numbers.
Q3: Are there other methods to find the GCF besides the ones mentioned?
A3: Yes, there are more advanced algorithms for calculating the GCF, particularly for very large numbers, often utilized in computational number theory. These algorithms are often based on more sophisticated mathematical principles.
Q4: How is the GCF useful in real-world applications?
A4: The GCF finds application in various fields as highlighted earlier, including simplifying fractions, solving problems involving ratios and proportions, cryptography, computer science, and geometry.
Conclusion
Finding the greatest common factor of 8 and 32, while seemingly a simple arithmetic problem, opens a gateway to understanding fundamental concepts in number theory. We explored three methods—listing factors, prime factorization, and the Euclidean algorithm—each offering a different approach to solving this problem. We also emphasized the broader significance of the GCF and its relationship with the LCM, highlighting its practical applications across diverse fields. Understanding these concepts is not only crucial for mathematical proficiency but also extends to solving real-world problems and appreciating the elegance of number theory. This exploration illustrates the depth and breadth of even seemingly simple mathematical concepts, encouraging a deeper dive into the fascinating world of numbers and their relationships.
Latest Posts
Latest Posts
-
What Is Equivalent To 612
Sep 12, 2025
-
Delta C To Delta F
Sep 12, 2025
-
What Is 30 Off 60
Sep 12, 2025
-
Gcf Of 16 And 72
Sep 12, 2025
-
1 25 As A Percent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 8 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.