Half Of 2 3/4 Cups
saludintensiva
Sep 22, 2025 · 5 min read
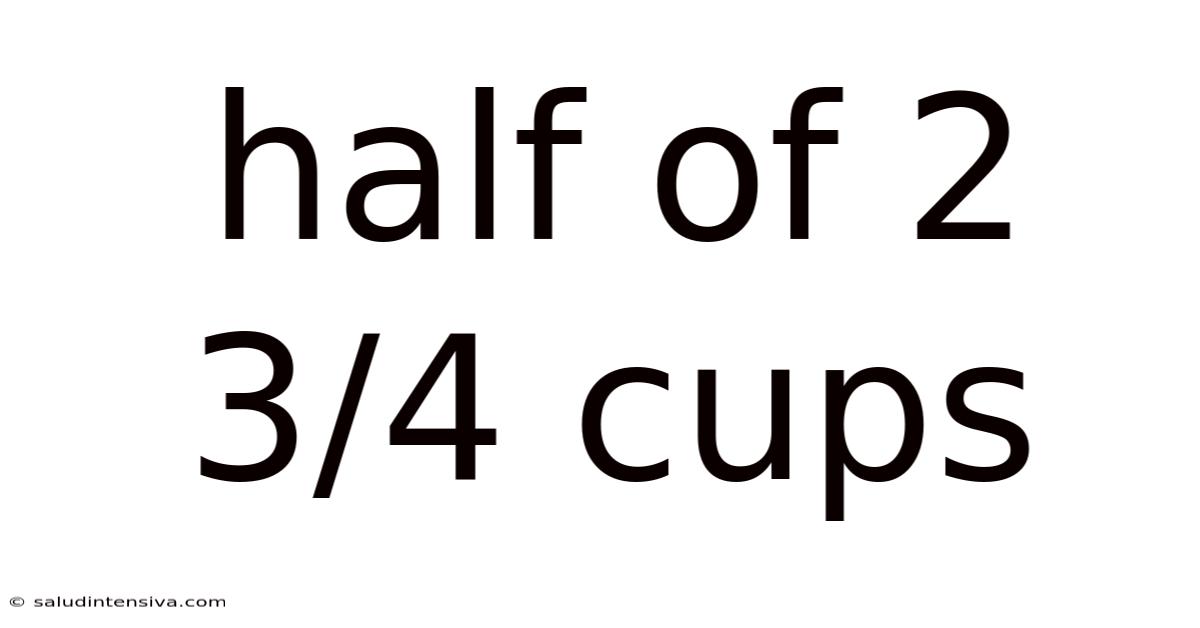
Table of Contents
Half of 2 3/4 Cups: A Deep Dive into Fractions and Measurement
Finding half of 2 3/4 cups might seem like a simple task, but it opens a door to understanding fundamental concepts in fractions, decimals, and practical measurement conversions. This seemingly straightforward calculation is a gateway to mastering more complex mathematical problems and everyday tasks in cooking, baking, and various other fields. This article provides a comprehensive guide, explaining the process in detail, addressing potential confusion, and extending the learning to related concepts.
Understanding the Problem: Half of 2 ¾ Cups
The core problem is calculating half the quantity of 2 ¾ cups. This requires a clear understanding of fractions and how to manipulate them. We're essentially looking for ½ * 2 ¾. While this might seem daunting at first, breaking it down into manageable steps makes it easily solvable.
Step-by-Step Solution: Finding the Answer
1. Convert the Mixed Fraction to an Improper Fraction:
The first step is to convert the mixed fraction 2 ¾ into an improper fraction. A mixed fraction combines a whole number and a fraction (e.g., 2 ¾). An improper fraction has a numerator larger than its denominator (e.g., 11/4).
To convert 2 ¾ to an improper fraction:
- Multiply the whole number (2) by the denominator (4): 2 * 4 = 8
- Add the numerator (3) to the result: 8 + 3 = 11
- Keep the same denominator (4): The improper fraction is 11/4.
Now our problem becomes: ½ * 11/4
2. Multiply the Fractions:
Multiplying fractions is straightforward. Multiply the numerators together and the denominators together:
- (1 * 11) / (2 * 4) = 11/8
3. Convert the Improper Fraction Back to a Mixed Fraction (Optional):
The result 11/8 is an improper fraction. While this is a perfectly valid answer, it's often more practical to convert it back into a mixed fraction for easier understanding in real-world applications.
To convert 11/8 to a mixed fraction:
- Divide the numerator (11) by the denominator (8): 11 ÷ 8 = 1 with a remainder of 3
- The whole number is the quotient (1).
- The remainder (3) becomes the new numerator.
- The denominator stays the same (8).
Therefore, 11/8 is equal to 1 ¾.
Conclusion of the Calculation: Half of 2 ¾ cups is 1 ¾ cups.
Visualizing the Solution: A Pictorial Representation
Imagine a measuring cup divided into quarters. Two and three-quarters cups would represent two full cups plus three quarters of a third cup. To find half, visually divide each of those quarters in half, creating eighths. Counting up the eighths reveals eleven in total. Dividing this by two would visually confirm 1 ¾ cups.
Extending the Understanding: Decimals and Measurement Conversions
This problem can also be solved using decimals. Converting the fractions to decimals provides another perspective and reinforces the connection between fractions and decimals.
1. Convert Fractions to Decimals:
- ¾ = 0.75 (3 divided by 4)
- 2 ¾ = 2.75
2. Calculate Half:
- 2.75 / 2 = 1.375
3. Convert the Decimal Back to a Fraction (Optional):
- 1.375 can be converted to a fraction:
- 0.375 is 375/1000. Simplifying this fraction by dividing both numerator and denominator by 125 gives us 3/8.
- Therefore, 1.375 = 1 3/8. Note that this is slightly different from the 1 ¾ we got earlier due to rounding errors.
This method highlights that while decimals offer a different approach, slight variations can occur due to rounding. In practical measurement, minor discrepancies are often acceptable.
Practical Applications: Cooking, Baking, and Beyond
Understanding how to halve recipes is crucial in cooking and baking. If a recipe calls for 2 ¾ cups of flour, knowing that half is 1 ¾ cups ensures accurate measurements and consistent results. This principle extends beyond culinary arts. It's relevant in any situation involving precise measurements, from construction and engineering to medicine and scientific experiments.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, a calculator can simplify the process, particularly when dealing with more complex fractions or decimals. However, understanding the underlying principles of fraction manipulation is crucial for broader mathematical comprehension.
Q: What if I need a third or a quarter of 2 ¾ cups?
A: The same principles apply. Convert the mixed fraction to an improper fraction, perform the multiplication, and then convert back to a mixed fraction if necessary.
Q: Are there any shortcuts for halving fractions?
A: While there aren't specific shortcuts, understanding the process of converting to improper fractions streamlines the calculation. Practice makes perfect, so the more you work with fractions, the faster and more intuitive the process becomes.
Q: Why are both 1 ¾ and 1 3/8 mentioned as answers, though slightly different?
A: The discrepancy arises from the rounding inherent in decimal conversions. The fraction method provides a more precise answer in this specific case.
Conclusion: Mastering Fractions and Measurements
Finding half of 2 ¾ cups is more than just a simple calculation. It's an exercise in understanding fundamental mathematical concepts, their practical application, and the importance of accuracy in various fields. By mastering these principles, you'll not only be able to solve similar problems but also build a stronger foundation in mathematics and its real-world relevance. The ability to confidently work with fractions is a valuable skill that transcends specific problems and empowers you to tackle more complex challenges with ease and precision. The journey from understanding the basic concepts to applying them in practical scenarios is a rewarding one, leading to increased confidence and a deeper appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
29 35 As A Percentage
Sep 22, 2025
-
Days Since June 4 2024
Sep 22, 2025
-
13 10 As A Decimal
Sep 22, 2025
-
Inch Lb To Ft Lbs
Sep 22, 2025
-
6 2 Percent As A Decimal
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 3/4 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.