Half Of 3/8 In Fraction
saludintensiva
Sep 20, 2025 · 6 min read
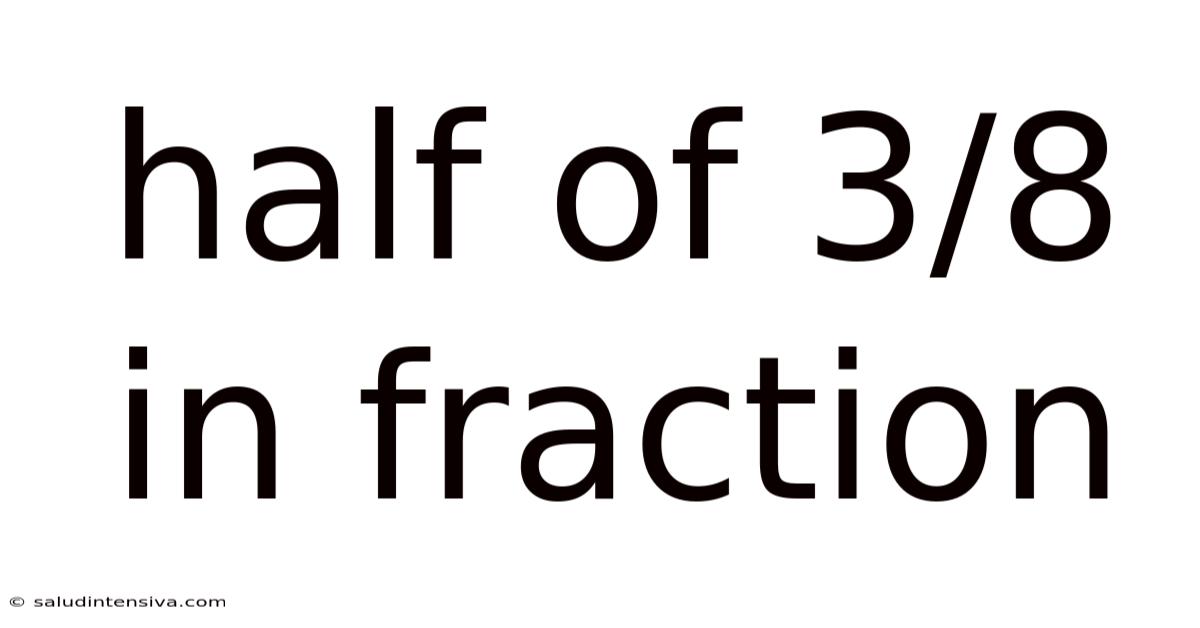
Table of Contents
Half of 3/8: A Deep Dive into Fraction Arithmetic
Finding half of 3/8 might seem like a simple task, especially for those comfortable with fractions. However, understanding this seemingly basic calculation opens the door to a broader comprehension of fraction arithmetic, including multiplication, division, and simplification. This article will not only show you how to solve "half of 3/8" but also delve into the underlying principles, providing you with a solid foundation in fraction manipulation. We'll explore various methods, tackle common misconceptions, and even address some frequently asked questions.
Introduction: Understanding Fractions
Before jumping into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 out of 8 equal parts of a whole.
Method 1: Direct Multiplication
The most straightforward way to find half of 3/8 is through multiplication. "Half" can be represented as the fraction 1/2. To find half of 3/8, we simply multiply the two fractions together:
(1/2) * (3/8) = (1 * 3) / (2 * 8) = 3/16
Therefore, half of 3/8 is 3/16.
This method highlights the fundamental rule of multiplying fractions: multiply the numerators together and then multiply the denominators together. This is a core concept in fraction arithmetic that applies to all fraction multiplications.
Method 2: Dividing by 2
Another approach involves dividing 3/8 by 2. Dividing by 2 is the same as multiplying by 1/2. This is because dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 2 is 1/2.
So, we can rewrite the problem as:
(3/8) / 2 = (3/8) * (1/2) = 3/16
Again, we arrive at the answer: 3/16. This method reinforces the relationship between division and multiplication with fractions, a crucial understanding for mastering fraction manipulation.
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for beginners. Imagine a circle divided into 8 equal slices (representing the denominator 8). Now, shade 3 of those slices (representing the numerator 3). To find half of 3/8, we need to find half of the shaded area. Dividing the shaded area in half means dividing each of the 3 shaded slices into two smaller slices. This results in 6 smaller slices out of a total of 16 smaller slices (8 original slices x 2). This visual representation leads to the fraction 6/16, which simplifies to 3/16.
This visual method connects the abstract concept of fractions to a concrete representation, making it easier to grasp the concept for visual learners.
Simplifying Fractions: A Crucial Step
While 3/16 is the correct answer, it's always good practice to simplify fractions to their lowest terms. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. In this case, 3 and 16 share no common factors other than 1, so 3/16 is already in its simplest form. However, let's consider an example where simplification is necessary.
Let's say we were finding half of 4/8. Following the same steps:
(1/2) * (4/8) = 4/16
Notice that both 4 and 16 are divisible by 4. We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4:
4/16 = (4 ÷ 4) / (16 ÷ 4) = 1/4
Therefore, half of 4/8 is 1/4. This illustrates the importance of simplifying fractions for clear and concise representation.
Common Misconceptions
One common mistake is to incorrectly find half of a fraction by halving only the numerator or the denominator. For example, some might incorrectly calculate half of 3/8 as 3/4 (halving the denominator) or 1.5/8 (halving the numerator). These are incorrect because they don't maintain the proportional relationship between the numerator and denominator. Remember, to find half of a fraction, you must either multiply by 1/2 or divide by 2, affecting both the numerator and the denominator proportionally.
Another misconception revolves around improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). The principles of finding half remain the same, even with improper fractions. For example, half of 5/4 would be (1/2) * (5/4) = 5/8.
Explanation of the Mathematical Principles
Finding half of a fraction fundamentally involves the multiplication of fractions. The operation relies on the commutative property of multiplication, which states that the order of factors does not change the product (a x b = b x a). This property allows us to multiply the fractions in any order. Furthermore, the procedure utilizes the concept of the multiplicative identity, where multiplying a number by 1 does not change its value. Since 1/2 is the equivalent of 0.5, we are effectively multiplying 3/8 by 0.5, which results in 3/16.
The simplification process, as previously shown, uses the concept of the greatest common divisor (GCD). Finding the GCD and dividing both the numerator and the denominator by it reduces the fraction to its simplest form without changing its value. This process is based on the principle of equivalence in fractions.
Frequently Asked Questions (FAQ)
-
Q: Can I find half of a fraction by dividing the numerator by 2? A: No, you cannot simply divide the numerator by 2. You must multiply the entire fraction by 1/2, which affects both the numerator and the denominator proportionally.
-
Q: What if the numerator is an odd number? A: Even if the numerator is an odd number, the process remains the same. You will still multiply by 1/2 and simplify the resulting fraction if possible.
-
Q: How do I handle mixed numbers? A: A mixed number is a whole number combined with a fraction (e.g., 1 1/2). To find half of a mixed number, first convert it into an improper fraction, then multiply by 1/2. For example, to find half of 1 1/2 (which is 3/2), you would calculate (1/2) * (3/2) = 3/4.
-
Q: Why is simplification important? A: Simplifying fractions makes them easier to understand and compare. It presents the fraction in its most concise form, facilitating calculations and making the result clearer.
Conclusion: Mastering Fraction Arithmetic
Finding half of 3/8, as demonstrated, is a fundamental operation that showcases essential principles in fraction arithmetic. Understanding the methods, addressing common misconceptions, and grasping the underlying mathematical principles empower you to confidently tackle more complex fraction problems. Remember the importance of simplifying fractions for clarity and efficiency. With practice, manipulating fractions becomes second nature, opening up a wider world of mathematical possibilities. This article served not only as a solution to a specific problem but also as a comprehensive guide to understanding and applying fundamental concepts in fraction arithmetic. Through understanding these core principles, you can confidently tackle a range of fraction-based problems and build a strong foundation in mathematics.
Latest Posts
Latest Posts
-
Where Is The Thousandths Place
Sep 20, 2025
-
Value Of 50 Cent Coins
Sep 20, 2025
-
1 21 As A Percentage
Sep 20, 2025
-
60 Days After March 1
Sep 20, 2025
-
0 45 Acres To Square Feet
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Half Of 3/8 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.