Hcf Of 15 And 18
saludintensiva
Sep 14, 2025 · 6 min read
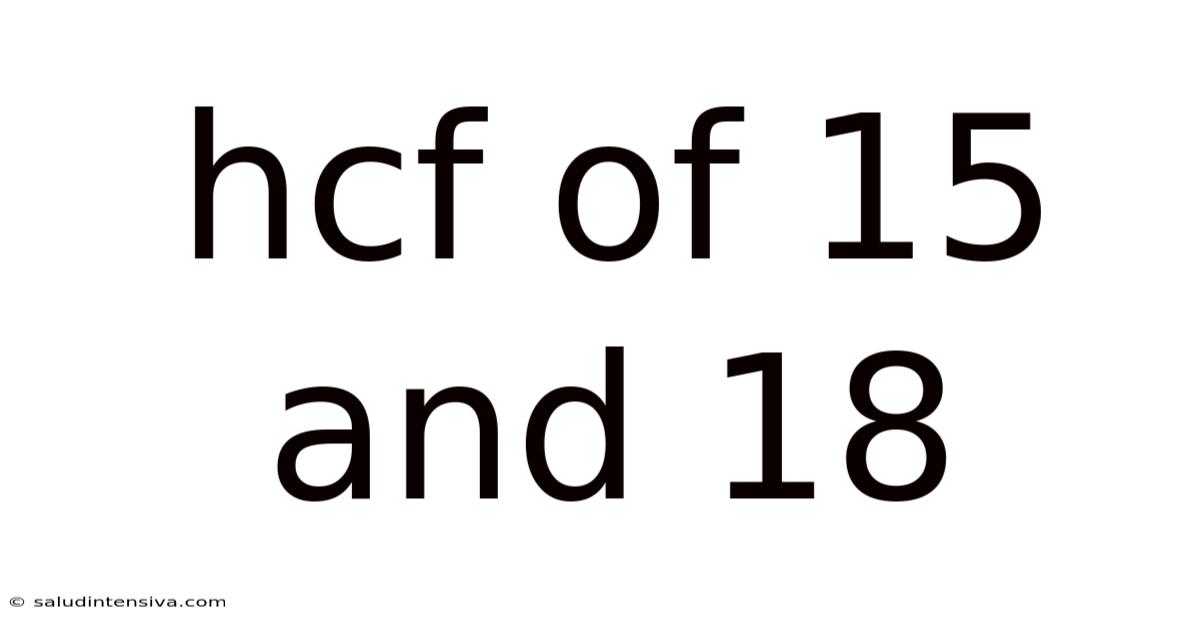
Table of Contents
Unveiling the Mysteries of HCF: A Deep Dive into Finding the Highest Common Factor of 15 and 18
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating HCF opens doors to more complex mathematical ideas and problem-solving skills. This article will delve into the process of finding the HCF of 15 and 18, exploring various methods, explaining the underlying principles, and highlighting the significance of HCF in various mathematical applications.
Understanding Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It's the biggest number that's a common factor to all the numbers in question. Think of it as the largest possible chunk you can divide your numbers into without having anything left over. For instance, if you have 15 apples and 18 oranges, and you want to divide them into equally sized groups, the largest group size you could have would be determined by the HCF of 15 and 18.
This concept is crucial in various mathematical fields, from simplifying fractions to solving algebraic equations and even understanding more advanced concepts like modular arithmetic.
Method 1: Prime Factorization Method
This is a fundamental method for finding the HCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 15 and 18:
- Prime Factorization of 15: 15 = 3 x 5
- Prime Factorization of 18: 18 = 2 x 3 x 3 = 2 x 3²
Now, we identify the common prime factors. Both 15 and 18 share one 3. The HCF is the product of these common prime factors.
Therefore, the HCF of 15 and 18 is 3.
Method 2: Listing Factors Method
This method is more straightforward, especially for smaller numbers. We list all the factors (numbers that divide evenly) of each number and then identify the largest common factor.
- Factors of 15: 1, 3, 5, 15
- Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the lists, we see that the common factors are 1 and 3. The largest common factor is 3.
Therefore, the HCF of 15 and 18 is 3. This method is simple for smaller numbers but becomes less efficient as numbers get larger.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, particularly useful for larger numbers where prime factorization becomes cumbersome. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until we reach a point where the remainder is zero. The last non-zero remainder is the HCF.
Let's apply the Euclidean algorithm to 15 and 18:
- Divide the larger number (18) by the smaller number (15): 18 = 15 x 1 + 3
- Replace the larger number (18) with the remainder (3): Now we find the HCF of 15 and 3.
- Divide 15 by 3: 15 = 3 x 5 + 0
- Since the remainder is 0, the HCF is the last non-zero remainder, which is 3.
Therefore, the HCF of 15 and 18 is 3 using the Euclidean algorithm. This method is computationally efficient and works flawlessly regardless of the size of the numbers.
Visualizing HCF with Venn Diagrams
We can visualize the HCF using Venn diagrams. Represent the factors of each number as circles. The overlapping section represents the common factors.
[Imagine a Venn diagram here: Circle 1 labelled "Factors of 15" containing 1, 3, 5, 15. Circle 2 labelled "Factors of 18" containing 1, 2, 3, 6, 9, 18. The overlapping section contains 1 and 3. The largest number in the overlapping section is the HCF, which is 3.]
The Significance of HCF
The HCF has far-reaching implications in various areas of mathematics and beyond:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we divide both the numerator and the denominator by their HCF. For example, the fraction 18/15 can be simplified to 6/5 by dividing both by their HCF, which is 3.
-
Solving Word Problems: Many word problems involving division and grouping rely on the concept of HCF. For example, problems related to distributing items equally among groups or finding the largest possible size of identical groups often require calculating the HCF.
-
Algebra and Number Theory: HCF plays a fundamental role in more advanced mathematical concepts like modular arithmetic, Diophantine equations, and the study of prime numbers.
-
Real-World Applications: HCF is applied in various real-world scenarios, including cutting materials into equal pieces, scheduling events with common intervals, and even in cryptography.
Frequently Asked Questions (FAQs)
Q1: What if the HCF of two numbers is 1?
A1: If the HCF of two numbers is 1, it means they are relatively prime or coprime. This signifies that they share no common factors other than 1.
Q2: Can the HCF of two numbers be larger than either of the numbers?
A2: No. The HCF is always less than or equal to the smaller of the two numbers.
Q3: Is there a formula to calculate HCF?
A3: There isn't a single, universally applicable formula for calculating HCF. The methods discussed earlier (prime factorization, listing factors, Euclidean algorithm) provide systematic approaches. However, formulas exist for specific cases, such as when the numbers are consecutive integers.
Q4: How can I find the HCF of more than two numbers?
A4: To find the HCF of more than two numbers, you can extend any of the methods discussed. For example, using the prime factorization method, you would find the prime factors of all the numbers and then identify the common prime factors with the lowest exponent. The Euclidean algorithm can be applied iteratively.
Conclusion: Mastering the HCF
Finding the Highest Common Factor is a fundamental skill in mathematics with far-reaching applications. Understanding the different methods – prime factorization, listing factors, and the Euclidean algorithm – allows for flexibility in tackling various problems. This knowledge isn't merely about arithmetic; it's a stepping stone to understanding more advanced mathematical concepts and applying logical reasoning to solve real-world problems. By mastering the concept of HCF, you're building a solid foundation for further exploration in the fascinating world of numbers. Remember, the beauty of mathematics lies in its interconnectedness, and the HCF serves as a perfect example of how a seemingly simple concept can unlock doors to a much broader understanding. So, keep exploring, keep questioning, and keep learning!
Latest Posts
Related Post
Thank you for visiting our website which covers about Hcf Of 15 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.