Hcf Of 2 And 3
saludintensiva
Sep 16, 2025 · 7 min read
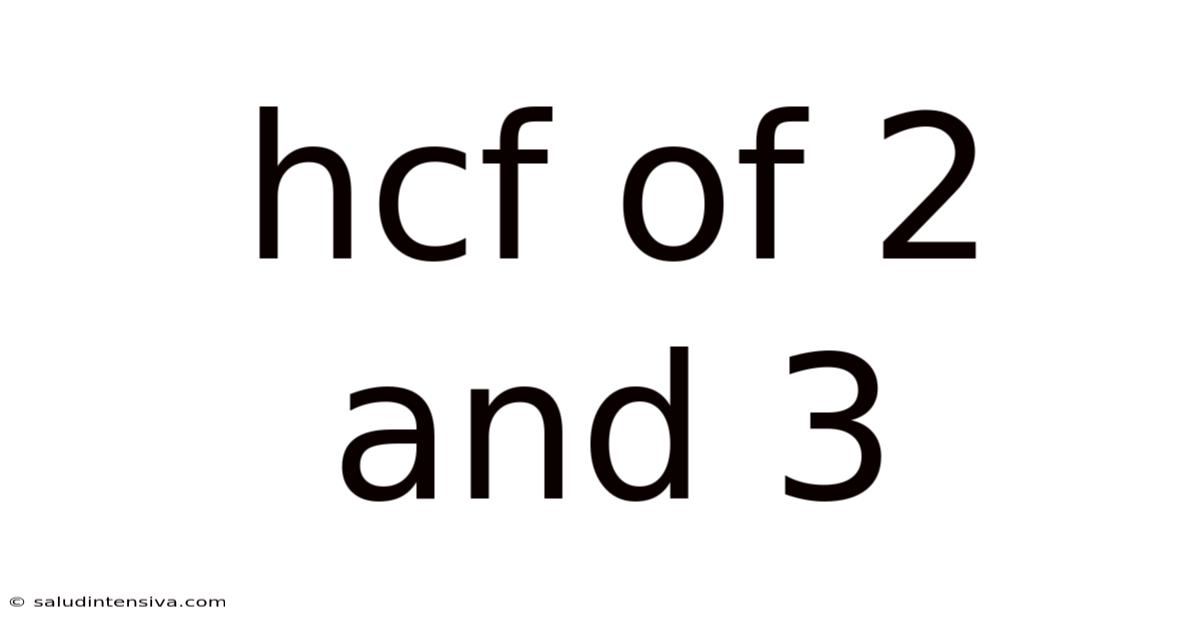
Table of Contents
Unveiling the Mysteries of the HCF: A Deep Dive into the Highest Common Factor of 2 and 3
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), might seem like a simple task, especially when dealing with small numbers like 2 and 3. However, understanding the underlying principles behind calculating the HCF is crucial for grasping more complex mathematical concepts. This article will not only determine the HCF of 2 and 3 but will also delve into the various methods for calculating HCFs, exploring their applications and significance in mathematics and beyond. We'll uncover the beauty of prime factorization, the efficiency of the Euclidean algorithm, and the intuitive understanding of the concept itself.
Introduction: What is the Highest Common Factor (HCF)?
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It represents the greatest common divisor shared amongst the numbers. Understanding the HCF is fundamental to simplifying fractions, solving algebraic equations, and working with various mathematical problems. For instance, in geometry, the HCF might be used to determine the largest square tile that can perfectly cover a rectangular floor.
Finding the HCF of 2 and 3: A Step-by-Step Approach
The numbers 2 and 3 are relatively small, allowing us to find their HCF using a simple, intuitive method. Let's examine the factors of each number:
- Factors of 2: 1, 2
- Factors of 3: 1, 3
The common factors of 2 and 3 are only 1. Therefore, the highest common factor (HCF) of 2 and 3 is 1.
This indicates that 2 and 3 are coprime or relatively prime, meaning they share no common factors other than 1.
Method 1: Prime Factorization Method
The prime factorization method is a powerful technique for finding the HCF of larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's apply this method to our numbers:
- Prime factorization of 2: 2 (2 is itself a prime number)
- Prime factorization of 3: 3 (3 is itself a prime number)
Since there are no common prime factors between 2 and 3, their HCF is 1. This reinforces our earlier finding.
This method becomes particularly useful when dealing with larger numbers. For example, let's find the HCF of 12 and 18:
- Prime factorization of 12: 2 x 2 x 3
- Prime factorization of 18: 2 x 3 x 3
The common prime factors are 2 and 3. Therefore, the HCF of 12 and 18 is 2 x 3 = 6.
Method 2: The Euclidean Algorithm
The Euclidean algorithm provides a more efficient method for finding the HCF, especially when dealing with larger numbers. It's based on the principle of repeated division. The algorithm proceeds as follows:
- Divide the larger number by the smaller number and find the remainder.
- Replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat steps 1 and 2 until the remainder is 0.
- The last non-zero remainder is the HCF.
Let's apply this to find the HCF of 12 and 18:
- 18 ÷ 12 = 1 with a remainder of 6.
- Now, we consider 12 and 6.
- 12 ÷ 6 = 2 with a remainder of 0.
The last non-zero remainder is 6, so the HCF of 12 and 18 is 6. This confirms our result from the prime factorization method.
Applying the Euclidean algorithm to 2 and 3:
- 3 ÷ 2 = 1 with a remainder of 1.
- Now, we consider 2 and 1.
- 2 ÷ 1 = 2 with a remainder of 0.
The last non-zero remainder is 1, so the HCF of 2 and 3 is 1.
The Significance of the HCF: Real-World Applications
The HCF isn't just a theoretical concept; it has practical applications in various fields:
-
Fraction Simplification: The HCF is essential for simplifying fractions to their lowest terms. For example, the fraction 12/18 can be simplified by dividing both the numerator and denominator by their HCF, which is 6, resulting in the simplified fraction 2/3.
-
Geometry: As mentioned earlier, the HCF can determine the size of the largest square tile that can perfectly cover a rectangular floor. If the dimensions of the floor are 12 units by 18 units, the largest square tile would have sides of length 6 units (the HCF of 12 and 18).
-
Number Theory: The HCF plays a vital role in various number theory concepts, including modular arithmetic, cryptography, and the study of prime numbers.
-
Computer Science: Algorithms for finding the HCF are used in computer science for tasks such as simplifying rational numbers, optimizing calculations, and solving certain types of equations.
Understanding Coprime Numbers
As we've seen with the example of 2 and 3, numbers that have an HCF of 1 are called coprime or relatively prime. This means they share no common factors other than 1. Understanding coprime numbers is important in various mathematical contexts, particularly in number theory and cryptography.
Beyond Two Numbers: Finding the HCF of Multiple Numbers
The methods described above can be extended to find the HCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and identify the common prime factors with the lowest power. For the Euclidean algorithm, you would repeatedly apply the algorithm to pairs of numbers until you find the HCF of all numbers.
For example, let's find the HCF of 12, 18, and 24:
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
- Prime factorization of 24: 2³ x 3
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the HCF of 12, 18, and 24 is 2 x 3 = 6.
Frequently Asked Questions (FAQ)
-
Q: What if the HCF of two numbers is one of the numbers?
- A: This simply means that the smaller number divides the larger number evenly. For example, the HCF of 6 and 12 is 6.
-
Q: Can the HCF of two numbers be zero?
- A: No, the HCF of two numbers can never be zero. The HCF is always a positive integer.
-
Q: Is there a limit to how large the HCF of two numbers can be?
- A: No, there's no upper limit. The HCF can be arbitrarily large, depending on the numbers chosen.
-
Q: Why is the Euclidean algorithm more efficient for larger numbers?
- A: The prime factorization method can become computationally expensive for very large numbers because finding prime factors can be a time-consuming process. The Euclidean algorithm is more efficient because it doesn't require finding prime factors.
-
Q: Can I use a calculator to find the HCF?
- A: Many calculators have built-in functions to compute the HCF (or GCD). However, understanding the underlying methods remains crucial for grasping the mathematical concept.
Conclusion: Mastering the HCF
Understanding the Highest Common Factor is a cornerstone of number theory and has practical applications in various fields. This article has explored different methods for calculating the HCF, emphasizing the intuitive approach for smaller numbers and the more efficient Euclidean algorithm for larger ones. By grasping these methods and their underlying principles, you will not only be able to calculate HCFs effectively but also gain a deeper appreciation for the interconnectedness of mathematical concepts. Remember that practice is key to mastering this fundamental concept. Work through various examples, and don't hesitate to explore further resources to deepen your understanding. The journey of mathematical discovery is a continuous one, and the HCF is a valuable stepping stone along the way.
Latest Posts
Latest Posts
-
Convertidor Temperatura F A C
Sep 16, 2025
-
Gcf Of 8 And 9
Sep 16, 2025
-
Gcf Of 30 And 5
Sep 16, 2025
-
71 M2 To Square Feet
Sep 16, 2025
-
9 10 Is What Percent
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 2 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.