Is 1/2 Bigger Than 3/5
saludintensiva
Sep 15, 2025 · 5 min read
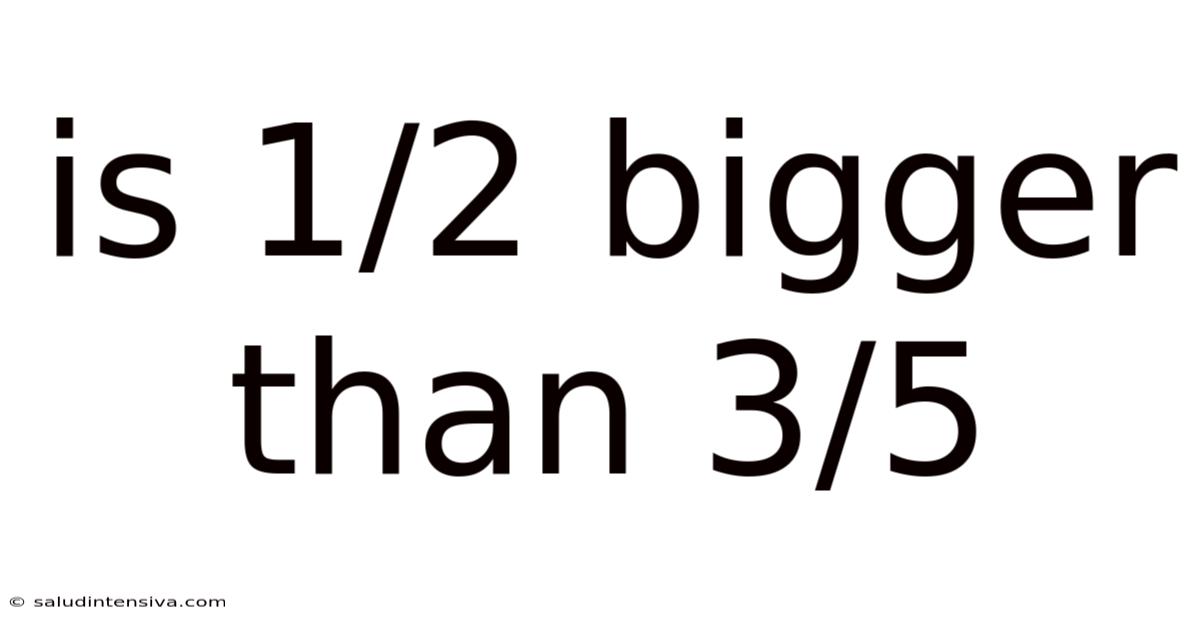
Table of Contents
Is 1/2 Bigger Than 3/5? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will explore the question, "Is 1/2 bigger than 3/5?", providing a comprehensive explanation that goes beyond a simple yes or no answer. We will delve into various methods for comparing fractions, explore the underlying concepts, and address common misconceptions. By the end, you'll not only know the answer but also possess a robust understanding of fraction comparison techniques.
Introduction: Understanding Fractions
Before tackling the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, representing one out of two equal parts.
Comparing fractions requires understanding their relative sizes. This can be challenging because, unlike whole numbers, the size of a fraction isn't immediately obvious. Several methods exist to determine which fraction is larger.
Method 1: Finding a Common Denominator
This is perhaps the most common and reliable method for comparing fractions. The principle is to convert both fractions to equivalent fractions with the same denominator. This allows for a direct comparison of the numerators.
Let's apply this to our problem: Is 1/2 bigger than 3/5?
-
Find the least common multiple (LCM) of the denominators: The denominators are 2 and 5. The LCM of 2 and 5 is 10.
-
Convert each fraction to an equivalent fraction with a denominator of 10:
- For 1/2, we multiply both the numerator and the denominator by 5: (1 x 5) / (2 x 5) = 5/10
- For 3/5, we multiply both the numerator and the denominator by 2: (3 x 2) / (5 x 2) = 6/10
-
Compare the numerators: Now we have 5/10 and 6/10. Since 6 > 5, we conclude that 6/10 is larger than 5/10.
-
Conclusion: Therefore, 3/5 (which is equivalent to 6/10) is bigger than 1/2 (which is equivalent to 5/10).
Method 2: Converting to Decimals
Another effective method is to convert both fractions to decimals. This involves dividing the numerator by the denominator.
-
Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
-
Convert 3/5 to a decimal: 3 ÷ 5 = 0.6
-
Compare the decimals: Since 0.6 > 0.5, we conclude that 3/5 is larger than 1/2.
Method 3: Visual Representation
While not always practical for complex fractions, visualizing fractions can be helpful, especially for beginners. Imagine a pizza cut into equal slices.
- 1/2: Represents one slice of a pizza cut into two equal slices.
- 3/5: Represents three slices of a pizza cut into five equal slices.
Visually comparing these scenarios, it becomes apparent that three out of five slices (3/5) represent a larger portion than one out of two slices (1/2).
Method 4: Cross-Multiplication
This method provides a quick way to compare fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other, and vice versa.
-
Cross-multiply:
- Multiply the numerator of 1/2 (which is 1) by the denominator of 3/5 (which is 5): 1 x 5 = 5
- Multiply the numerator of 3/5 (which is 3) by the denominator of 1/2 (which is 2): 3 x 2 = 6
-
Compare the results: Since 6 > 5, the fraction with the larger product (3/5) is the larger fraction.
Addressing Common Misconceptions
A common misconception is that a larger numerator always indicates a larger fraction. This is only true if the denominators are the same. Comparing 1/2 and 3/5 highlights this; although 3 > 1, 3/5 is larger because the denominator also influences the overall size.
Another misconception revolves around the difficulty of comparing fractions with different denominators. While it may seem more complex, the methods outlined above provide clear and reliable strategies to overcome this challenge.
Further Exploration: Working with Improper Fractions and Mixed Numbers
The methods discussed above apply equally to improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction).
For example, let's compare 7/4 and 1 2/5.
-
Convert to improper fractions: 1 2/5 = (5 x 1 + 2) / 5 = 7/5
-
Use any of the methods above (common denominator, decimals, cross-multiplication) to compare 7/4 and 7/5. Using the common denominator method, we get 35/20 and 28/20. Therefore, 7/4 is bigger.
Conclusion: Mastering Fraction Comparison
Determining whether 1/2 is bigger than 3/5 requires a systematic approach. Through the application of various methods—finding a common denominator, converting to decimals, visualizing, or cross-multiplying—we can confidently conclude that 3/5 is bigger than 1/2. This understanding extends beyond a simple comparison; it demonstrates a fundamental understanding of fraction manipulation and lays the foundation for more complex mathematical concepts. The key is to choose the method you find most comfortable and apply it consistently to achieve accurate comparisons. By mastering these techniques, you will build a solid foundation in fractions and confidently tackle more advanced mathematical problems.
Frequently Asked Questions (FAQ)
-
Q: Why is finding a common denominator the most reliable method? A: Because it allows for a direct comparison of numerators once both fractions are expressed in the same units (denominators).
-
Q: Can I always use cross-multiplication? A: Yes, cross-multiplication is a reliable method for comparing two fractions directly.
-
Q: What if the fractions are very large? A: Converting to decimals can be a more efficient method for larger fractions.
-
Q: Are there any other ways to compare fractions? A: While less common, methods like using fraction circles or number lines can aid visual understanding, especially for beginners.
-
Q: Is there a single "best" method? A: The best method depends on personal preference and the specific fractions being compared. Familiarity with multiple methods provides flexibility and problem-solving efficiency.
Latest Posts
Latest Posts
-
15 20 As A Percent
Sep 15, 2025
-
All The Factors Of 24
Sep 15, 2025
-
Is 1 3 Bigger Than 1 4
Sep 15, 2025
-
Is 1 8 Bigger Than 1 2
Sep 15, 2025
-
35 Percent Into A Fraction
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Bigger Than 3/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.