Is 1/2 Equivalent To 2/4
saludintensiva
Sep 13, 2025 · 6 min read
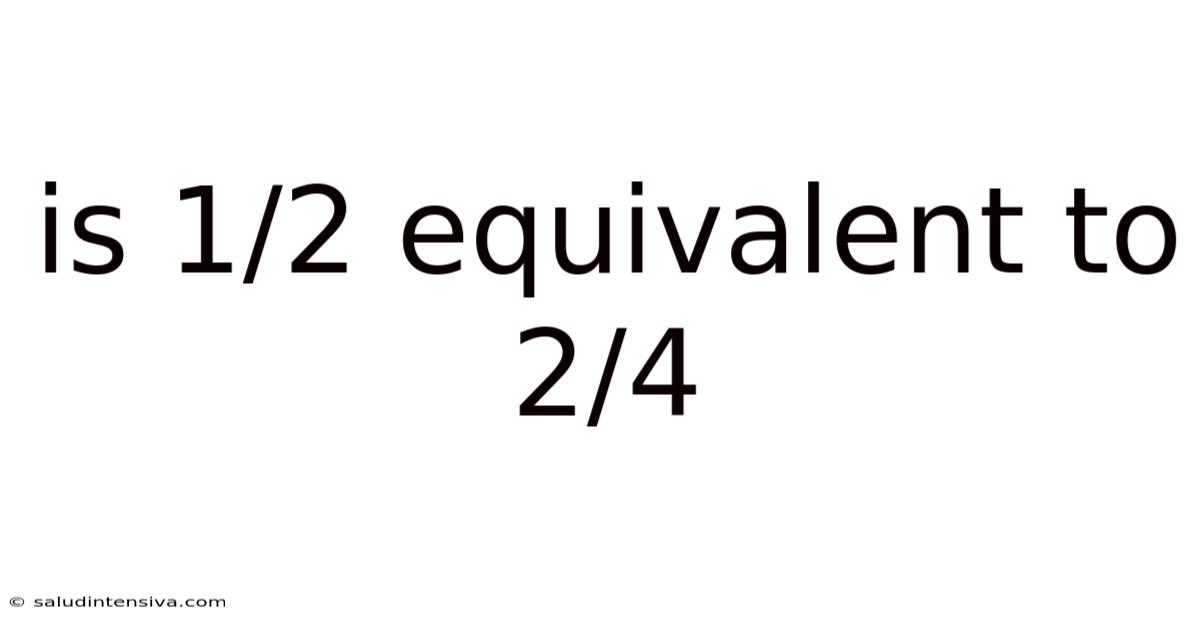
Table of Contents
Is 1/2 Equivalent to 2/4? A Deep Dive into Fractions
Are you struggling with fractions? Understanding the equivalence of fractions is a fundamental concept in mathematics. This article will thoroughly explore the question: Is 1/2 equivalent to 2/4? We'll delve into the concept of equivalent fractions, explore different methods to verify equivalence, and examine the underlying mathematical principles. By the end, you'll not only know the answer but also possess a solid understanding of fraction equivalence, empowering you to tackle more complex fraction problems with confidence. This comprehensive guide will also address frequently asked questions and provide practical examples to solidify your understanding.
Understanding Fractions: A Quick Recap
Before we dive into the equivalence of 1/2 and 2/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is written in the form a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 1/2, 1 represents the numerator and 2 represents the denominator. This signifies that we have one out of two equal parts.
Equivalent Fractions: The Core Concept
Equivalent fractions represent the same proportion or value, even though they look different. Think of it like this: slicing a pizza into four equal slices and taking two slices is exactly the same as slicing the same pizza into two equal slices and taking one. You've consumed the same amount of pizza in both scenarios. This is the essence of equivalent fractions. They represent the same amount, just expressed differently.
Is 1/2 Equivalent to 2/4? The Proof
Yes, 1/2 is equivalent to 2/4. We can demonstrate this equivalence through several methods:
1. Visual Representation:
Imagine a rectangular bar divided into two equal parts. Shading one part represents 1/2. Now, imagine the same rectangular bar divided into four equal parts. Shading two of those parts represents 2/4. Visually, the shaded area in both scenarios is identical, proving that 1/2 and 2/4 represent the same proportion of the whole.
2. Simplifying Fractions:
Simplifying a fraction involves finding an equivalent fraction by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD of 2 and 4 is 2. Dividing both the numerator and denominator of 2/4 by 2 gives us:
(2 ÷ 2) / (4 ÷ 2) = 1/2
This shows that 2/4 simplifies to 1/2, directly confirming their equivalence.
3. Multiplying Fractions:
We can also demonstrate equivalence by multiplying both the numerator and denominator of a fraction by the same non-zero number. This process doesn't change the value of the fraction, only its representation.
Multiplying both the numerator and denominator of 1/2 by 2 gives us:
(1 × 2) / (2 × 2) = 2/4
This confirms that 1/2 and 2/4 are equivalent fractions.
Beyond 1/2 and 2/4: Exploring Other Equivalent Fractions
The principles demonstrated with 1/2 and 2/4 apply to all fractions. Many fractions can be equivalent to each other. For instance:
- 1/3 = 2/6 = 3/9 = 4/12... and so on. Each of these fractions represents one-third of a whole.
- 2/5 = 4/10 = 6/15 = 8/20... These all represent two-fifths of a whole.
Finding equivalent fractions is crucial for various mathematical operations, such as adding and subtracting fractions with different denominators. To add fractions, they must have a common denominator. Finding equivalent fractions allows us to rewrite fractions with different denominators into fractions with a common denominator, making addition and subtraction possible.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions isn't just an academic exercise. It has numerous practical applications in everyday life, including:
-
Cooking and Baking: Recipes often require adjustments based on the number of servings. Understanding equivalent fractions allows you to accurately scale recipes up or down. If a recipe calls for 1/2 cup of sugar and you want to double the recipe, you know you need 2/4 cups (which is equivalent to 1 cup).
-
Measurement and Construction: In construction or any field involving precise measurements, understanding fractions and equivalent fractions is essential for accuracy and consistency. Converting between different units of measurement often involves working with equivalent fractions.
-
Data Analysis and Interpretation: Understanding fractions is vital for interpreting data represented in graphs and charts. Often data is presented as percentages or proportions, which are essentially fractions.
-
Financial Calculations: Many financial calculations, such as calculating interest rates or discounts, involve working with fractions and percentages.
The Importance of Simplifying Fractions
While equivalent fractions are useful, simplifying fractions to their lowest terms is often preferred. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. This makes it easier to understand and work with the fraction. Simplifying fractions is essentially finding the equivalent fraction with the smallest possible numerator and denominator. For example, 2/4 simplifies to 1/2, and 6/9 simplifies to 2/3.
Frequently Asked Questions (FAQ)
Q1: How can I find equivalent fractions easily?
A1: To find equivalent fractions, multiply or divide both the numerator and denominator by the same non-zero number. For example, to find an equivalent fraction of 1/2, you could multiply both by 2 (resulting in 2/4), by 3 (resulting in 3/6), and so on. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
Q2: Are there infinite equivalent fractions for any given fraction?
A2: Yes, except for fractions where the numerator is zero. You can always find another equivalent fraction by multiplying the numerator and denominator by any non-zero number.
Q3: Why is simplifying fractions important?
A3: Simplifying fractions makes them easier to understand and work with. It gives a clearer representation of the proportion and simplifies further calculations.
Q4: Can I add fractions without finding equivalent fractions with common denominators?
A4: No, adding or subtracting fractions requires a common denominator. You must find equivalent fractions that share the same denominator before performing the addition or subtraction.
Conclusion: Mastering Fraction Equivalence
Understanding the equivalence of fractions, such as the equivalence between 1/2 and 2/4, is a fundamental skill in mathematics with wide-ranging practical applications. Through visual representation, simplification, and multiplication, we have definitively shown that 1/2 and 2/4 are indeed equivalent. Mastering this concept provides a solid foundation for tackling more complex fraction problems, fostering confidence and proficiency in mathematical reasoning. Remember, practice makes perfect! The more you work with fractions, the more comfortable and confident you'll become in understanding and applying this crucial mathematical concept. By understanding the principles discussed in this article, you'll be well-equipped to handle fractions with ease and accuracy in all aspects of your life.
Latest Posts
Latest Posts
-
What Is Equal To 1 6
Sep 13, 2025
-
506 709 In Word Form
Sep 13, 2025
-
3 000 In Roman Numerals
Sep 13, 2025
-
12 8 As A Mixed Number
Sep 13, 2025
-
1 4 Of 3 4
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Equivalent To 2/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.