Is 1/2 Greater Than 1
saludintensiva
Sep 16, 2025 · 6 min read
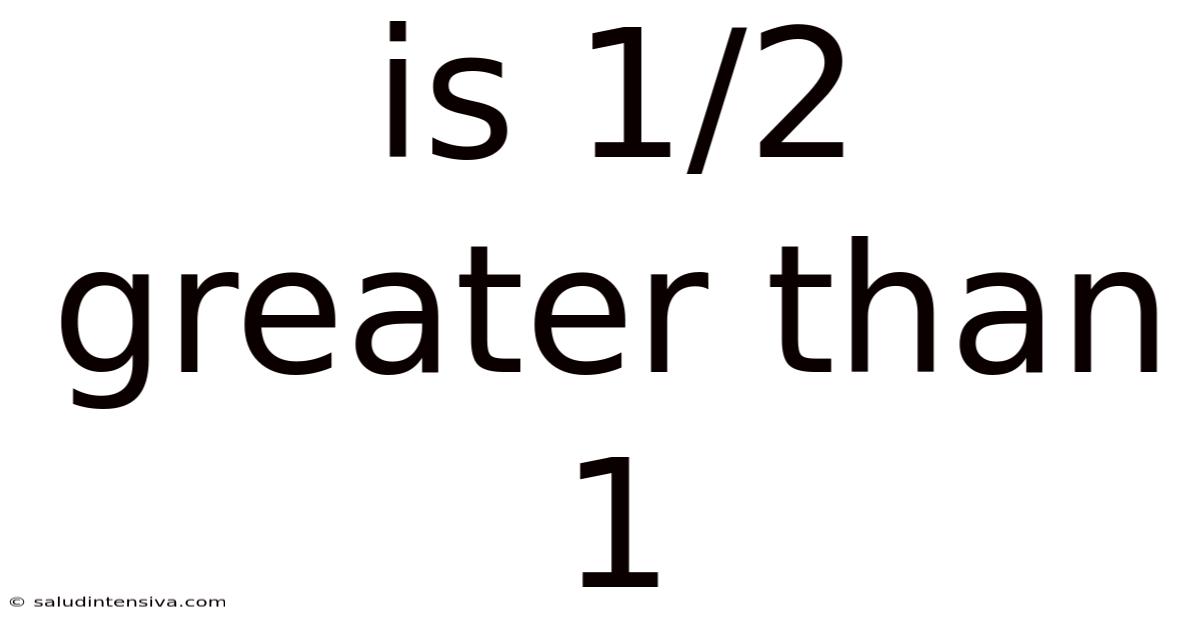
Table of Contents
Is 1/2 Greater Than 1? Understanding Fractions and Comparisons
Is 1/2 greater than 1? The simple answer is no. This seemingly straightforward question actually opens the door to understanding fundamental concepts in mathematics, particularly the nature of fractions and how to compare their values. This article will delve into the intricacies of fractions, explaining why 1/2 is less than 1, and providing a comprehensive guide to comparing fractions and other numbers. We'll cover various methods, exploring both intuitive approaches and more formal mathematical reasoning.
Understanding Fractions: Parts of a Whole
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/2, the denominator (2) means the whole is divided into two equal parts. The numerator (1) indicates that we are considering one of those parts. Therefore, 1/2 represents one-half of a whole.
To visualize this, imagine a pizza cut into two equal slices. 1/2 represents one slice of that pizza. The whole pizza is represented by the number 1. Clearly, one slice (1/2) is smaller than the entire pizza (1).
Comparing Fractions to Whole Numbers
Whole numbers represent complete units. Numbers like 1, 2, 3, and so on, represent one whole, two wholes, three wholes, and so forth. Fractions, on the other hand, represent parts of a whole.
When comparing a fraction to a whole number, it's crucial to understand that the fraction will always be less than the whole number unless the numerator is equal to or greater than the denominator. In such a case, the fraction represents one or more whole units.
For instance:
- 1/2 < 1: One-half is less than one whole.
- 3/4 < 1: Three-quarters is less than one whole.
- 5/4 > 1: Five-quarters is greater than one whole (it's equivalent to 1 and 1/4).
- 7/7 = 1: Seven-sevenths is equal to one whole.
Visualizing the Comparison: Using Diagrams
Diagrams can be incredibly helpful in understanding fraction comparisons. Let's visualize 1/2 and 1 using simple shapes:
Imagine a circle representing the whole (1). To represent 1/2, divide the circle into two equal parts and shade one part. It's immediately obvious that the shaded portion (1/2) is smaller than the entire circle (1).
Mathematical Methods for Comparing Fractions
While visualization is helpful, especially for introductory understanding, more formal mathematical methods are necessary for comparing more complex fractions. Here are a few key approaches:
-
Finding a Common Denominator: This is a fundamental technique for comparing fractions with different denominators. The goal is to rewrite the fractions so they have the same denominator. This allows for a direct comparison of the numerators.
For example, to compare 1/2 and 3/5, we find the least common multiple (LCM) of the denominators 2 and 5, which is 10. We then rewrite the fractions:
1/2 = 5/10 (multiply numerator and denominator by 5) 3/5 = 6/10 (multiply numerator and denominator by 2)
Now, we can easily see that 6/10 > 5/10, meaning 3/5 > 1/2.
-
Converting to Decimals: Another approach involves converting the fractions to decimals. To convert a fraction to a decimal, divide the numerator by the denominator.
For example:
1/2 = 1 ÷ 2 = 0.5 1 = 1.0
Comparing 0.5 and 1.0, it's clear that 0.5 < 1.0, confirming that 1/2 < 1.
-
Cross-Multiplication: This method is particularly useful for comparing two fractions directly without finding a common denominator. Cross-multiply the numerator of one fraction by the denominator of the other, and vice-versa. The larger product corresponds to the larger fraction.
Comparing 1/2 and 2/3:
1 x 3 = 3 2 x 2 = 4
Since 4 > 3, we conclude that 2/3 > 1/2.
Addressing Potential Misconceptions
One common misconception arises from thinking about the numbers individually. Students might focus on the fact that the numerator in 1/2 (which is 1) is smaller than the whole number 1, and incorrectly conclude that the fraction is larger. However, it's crucial to remember that the denominator plays a crucial role in determining the value of the fraction. The denominator defines the size of the parts, affecting the overall value.
Another misconception might involve comparing fractions with different denominators without finding a common denominator. Simply comparing numerators without considering the denominators can lead to inaccurate conclusions.
Extending the Concept: Comparing Fractions, Decimals, and Percentages
The principles discussed above can be extended to compare fractions with decimals and percentages. Remember that decimals and percentages are simply different ways of representing parts of a whole. To compare them, it's often helpful to convert them all to the same format (e.g., all to decimals or all to fractions).
Real-World Applications
Understanding fraction comparison is crucial in numerous real-world situations:
- Cooking and Baking: Recipes often require precise measurements, involving fractions of cups, tablespoons, or teaspoons.
- Construction and Engineering: Accurate measurements are paramount in construction and engineering, where fractions are used extensively.
- Finance: Calculating interest rates, discounts, and shares often involve fractions and decimals.
- Data Analysis: Fractions and percentages are frequently used to represent data and analyze trends.
Frequently Asked Questions (FAQ)
-
Q: Is any fraction with a numerator of 1 always less than 1? A: Yes, as long as the denominator is greater than 1. A fraction with a numerator of 1 and a denominator greater than 1 will always represent a part of a whole, and therefore be less than 1.
-
Q: How do I compare fractions with different numerators and denominators? A: The best approach is usually to find a common denominator or convert the fractions to decimals for comparison. Cross-multiplication also provides a direct method.
-
Q: Can a fraction be greater than 1? A: Yes, if the numerator is greater than the denominator. Such fractions represent more than one whole.
-
Q: What if the numerator and denominator are the same? A: If the numerator and denominator are equal, the fraction is equal to 1.
Conclusion
The question "Is 1/2 greater than 1?" serves as a springboard for understanding the fundamental concepts of fractions and their comparison. While the answer is a simple "no," the process of arriving at this answer involves grasping the meaning of fractions, visualizing their representation, and employing various mathematical techniques for comparison. Mastering these skills is essential for success in mathematics and its various applications in the real world. By understanding the relationship between fractions, decimals, and whole numbers, we can confidently navigate numerical comparisons and solve a wide array of mathematical problems. Remember to always consider the role of both the numerator and the denominator when evaluating the value of a fraction.
Latest Posts
Latest Posts
-
85 Degrees F In C
Sep 16, 2025
-
Lcm Of 42 And 14
Sep 16, 2025
-
Convert 105 F To Celsius
Sep 16, 2025
-
Cash 4 Life Numbers Generator
Sep 16, 2025
-
Gcf Of 6 And 2
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.