Is 1/3 Bigger Than 2/5
saludintensiva
Sep 18, 2025 · 5 min read
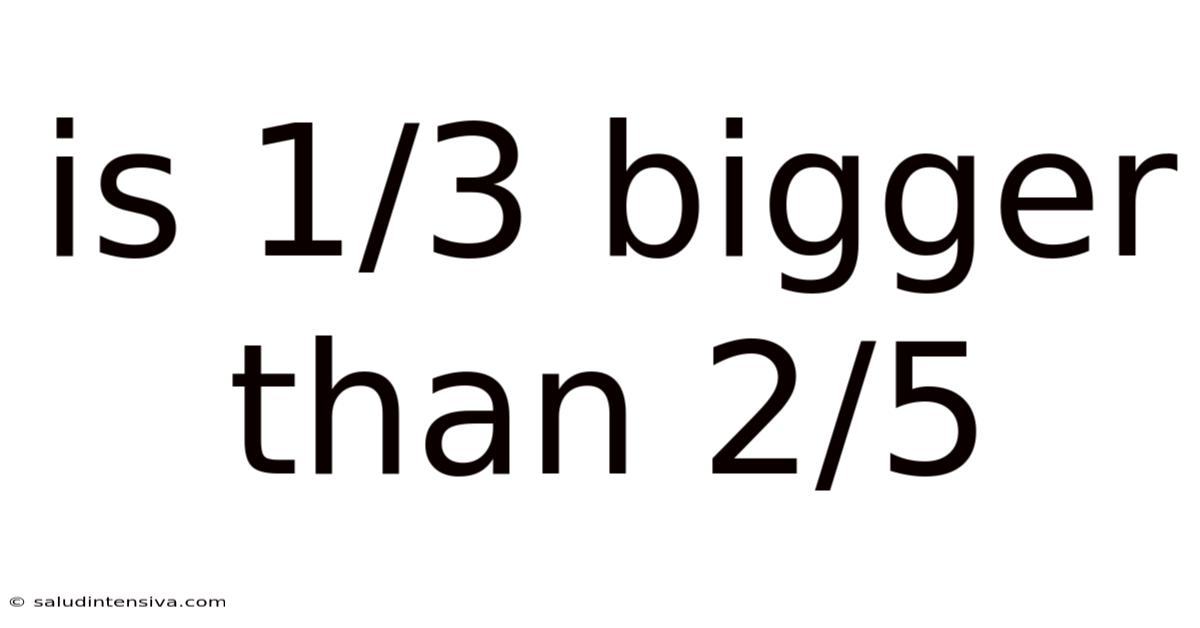
Table of Contents
Is 1/3 Bigger Than 2/5? A Deep Dive into Fraction Comparison
Determining whether 1/3 is bigger than 2/5 might seem like a simple question, but it's a gateway to understanding fundamental concepts in mathematics, particularly fractions. This comprehensive guide will not only answer this question definitively but also equip you with the tools and understanding to compare any two fractions with confidence. We'll explore various methods, delve into the underlying mathematical principles, and address common misconceptions. This is more than just a simple answer; it's a journey into the world of fractions.
Understanding Fractions: A Quick Refresher
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) tells us we have one part, and the denominator (3) tells us the whole is divided into three equal parts.
Method 1: Finding a Common Denominator
This is perhaps the most common and straightforward method for comparing fractions. The goal is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 1/3 and 2/5, we need to find the least common multiple (LCM) of 3 and 5. The LCM is the smallest number that is a multiple of both 3 and 5. In this case, the LCM of 3 and 5 is 15.
Now, we rewrite both fractions with a denominator of 15:
- 1/3: To change the denominator from 3 to 15, we multiply both the numerator and the denominator by 5: (1 x 5) / (3 x 5) = 5/15
- 2/5: To change the denominator from 5 to 15, we multiply both the numerator and the denominator by 3: (2 x 3) / (5 x 3) = 6/15
Now that both fractions have the same denominator, we can compare their numerators directly. Since 5 < 6, we conclude that 5/15 < 6/15, which means 1/3 < 2/5. Therefore, 1/3 is not bigger than 2/5; it is smaller.
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimals. This involves dividing the numerator by the denominator for each fraction.
- 1/3: 1 ÷ 3 ≈ 0.333... (a repeating decimal)
- 2/5: 2 ÷ 5 = 0.4
By comparing the decimal representations, we see that 0.333... < 0.4. This confirms that 1/3 < 2/5.
Method 3: Visual Representation
A visual approach can be particularly helpful for understanding fraction comparisons, especially for those who are visual learners. Imagine two identical pies.
- Pie 1: Cut the pie into 3 equal slices. 1/3 represents one of these slices.
- Pie 2: Cut the pie into 5 equal slices. 2/5 represents two of these slices.
Visually comparing the size of one slice from Pie 1 to two slices from Pie 2 will make it clear that two slices from a pie cut into five are larger than one slice from a pie cut into three. Again, this illustrates that 1/3 < 2/5.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is a crucial skill in various aspects of life and numerous academic subjects. From baking (following recipes accurately) to understanding financial data (analyzing percentages and proportions), fraction comparison is an essential tool. It also forms the foundation for more advanced mathematical concepts like algebra and calculus.
Addressing Common Misconceptions
Many people make the mistake of comparing fractions solely based on their numerators or denominators without considering the relationship between them. For instance, some might incorrectly assume that because 2 (the numerator of 2/5) is larger than 1 (the numerator of 1/3), 2/5 must be larger. This is incorrect; the denominator plays an equally crucial role.
Beyond 1/3 and 2/5: Comparing Any Two Fractions
The methods described above—finding a common denominator, converting to decimals, and visual representation—can be applied to compare any two fractions. Regardless of the complexity of the fractions, these methods provide a reliable and systematic approach.
Frequently Asked Questions (FAQs)
Q: Is there a shortcut for comparing fractions?
A: While there isn't a universally applicable shortcut, understanding the relationship between the numerator and denominator helps. If two fractions have the same denominator, the fraction with the larger numerator is larger. If two fractions have the same numerator, the fraction with the smaller denominator is larger. However, for fractions with different numerators and denominators, using the methods described above is most reliable.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various examples, use different comparison methods, and try to visualize the fractions. Online resources, educational apps, and practice worksheets can also greatly enhance your understanding.
Q: Are there other methods for comparing fractions?
A: Yes, there are other methods, including using cross-multiplication. Cross-multiplication involves multiplying the numerator of one fraction by the denominator of the other and comparing the results. However, this method can be more prone to errors, and the common denominator method is generally preferred for its clarity and simplicity.
Conclusion: Mastering Fractions
Comparing fractions is a fundamental skill in mathematics that extends far beyond simple exercises. Understanding the different methods—finding common denominators, converting to decimals, and visual representations—provides you with a powerful toolkit to tackle various fractional comparisons confidently. By mastering this skill, you're not just improving your mathematical abilities; you're building a stronger foundation for future mathematical endeavors and enhancing your problem-solving skills across many disciplines. Remember, the key is to practice regularly and to choose the method that you find most intuitive and reliable. Don't hesitate to revisit this guide as needed – the world of fractions awaits your exploration!
Latest Posts
Latest Posts
-
5 Minutes In An Hour
Sep 18, 2025
-
How To Simplify 3 4
Sep 18, 2025
-
Mean Of Grouped Data Calculator
Sep 18, 2025
-
28 Degrees Fahrenheit To Celsius
Sep 18, 2025
-
Kilometers To Miles Per Gallon
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 1/3 Bigger Than 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.