Is 1/4 Bigger Than 5/8
saludintensiva
Sep 13, 2025 · 5 min read
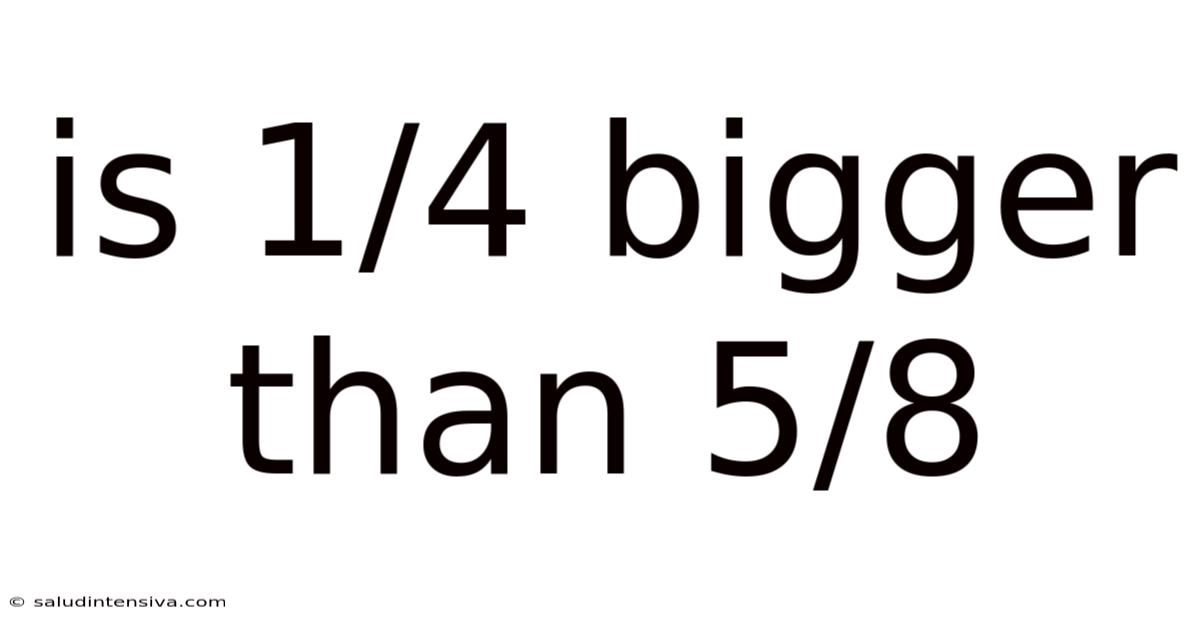
Table of Contents
Is 1/4 Bigger Than 5/8? Understanding Fractions and Comparisons
This article will delve into the seemingly simple question: Is 1/4 bigger than 5/8? While the answer might seem immediately obvious to some, understanding the underlying principles of fraction comparison is crucial for developing strong mathematical foundations. We'll explore various methods for comparing fractions, providing a clear and comprehensive explanation suitable for learners of all levels. This exploration will go beyond simply providing the answer, equipping you with the tools to confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 1/4, the numerator is 1, and the denominator is 4, meaning we have 1 out of 4 equal parts.
Method 1: Finding a Common Denominator
This is perhaps the most common and straightforward method for comparing fractions. The core idea is to rewrite both fractions so they share the same denominator. This allows for a direct comparison of their numerators.
To find a common denominator for 1/4 and 5/8, we look for the least common multiple (LCM) of 4 and 8. The multiples of 4 are 4, 8, 12, 16... and the multiples of 8 are 8, 16, 24... The LCM is 8.
Now, we rewrite 1/4 with a denominator of 8. To do this, we multiply both the numerator and the denominator by 2:
(1 x 2) / (4 x 2) = 2/8
Now we can compare 2/8 and 5/8. Since 2 is smaller than 5, we can conclude that:
2/8 < 5/8, therefore 1/4 < 5/8
1/4 is NOT bigger than 5/8.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into decimals. This is particularly useful when dealing with more complex fractions or when you're more comfortable working with decimal numbers.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
1/4 = 1 ÷ 4 = 0.25
5/8 = 5 ÷ 8 = 0.625
Comparing 0.25 and 0.625, it's clear that:
0.25 < 0.625, therefore 1/4 < 5/8
Again, we confirm that 1/4 is NOT bigger than 5/8.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially when working with fractions. Imagine a circle divided into four equal parts. Shading one part represents 1/4. Now, imagine another circle of the same size divided into eight equal parts. Shading five parts represents 5/8. A visual comparison clearly shows that the shaded area representing 5/8 is significantly larger than the shaded area representing 1/4.
This method is especially beneficial for younger learners or those who benefit from visual cues to understand mathematical concepts.
Method 4: Using Fraction Models
Fraction models like fraction bars, circles, or number lines can effectively visualize the size of each fraction. Representing 1/4 and 5/8 on a number line will demonstrate that 5/8 is to the right of 1/4, indicating a greater value.
These models provide a concrete representation, making abstract concepts more accessible and intuitive. They can help build a deeper understanding of fraction magnitudes and their relative sizes.
Why Understanding Fraction Comparison is Important
Mastering fraction comparison is a fundamental skill in mathematics. It's not just about solving isolated problems; it’s a building block for more advanced concepts. Here are some reasons why it's crucial:
- Foundation for Algebra: Understanding fractions is essential for solving algebraic equations and inequalities involving fractions.
- Real-World Applications: Fractions are prevalent in everyday life – from cooking and baking (measuring ingredients) to understanding proportions and percentages.
- Data Analysis: Interpreting data presented in fractional form is vital in various fields, including statistics and finance.
- Problem-Solving Skills: Comparing fractions enhances logical reasoning and problem-solving abilities, skills transferable to various aspects of life.
Extending the Understanding: Comparing More Complex Fractions
The methods discussed above can be applied to compare any two fractions, regardless of their complexity. For example, let's compare 7/12 and 2/3:
Method 1: Finding a Common Denominator
The LCM of 12 and 3 is 12. We rewrite 2/3 with a denominator of 12:
(2 x 4) / (3 x 4) = 8/12
Now, comparing 7/12 and 8/12, we see that 7/12 < 8/12. Therefore, 7/12 < 2/3.
Method 2: Converting to Decimals
7/12 = 7 ÷ 12 ≈ 0.583
2/3 = 2 ÷ 3 ≈ 0.667
Comparing the decimal values, we confirm that 0.583 < 0.667, therefore 7/12 < 2/3.
Frequently Asked Questions (FAQ)
Q: What if the fractions have different denominators and finding the LCM is difficult?
A: While finding the LCM is the most efficient method, you can always find a common denominator by multiplying the denominators together. This might result in a larger denominator than necessary, but it will still allow for accurate comparison.
Q: Are there other ways to compare fractions besides the ones mentioned?
A: Yes, there are other methods, but they often rely on a deeper understanding of fractions, such as cross-multiplication or comparing fractions to benchmark fractions like 1/2.
Q: How can I help my child understand fraction comparison?
A: Use visual aids, real-world examples, and hands-on activities. Start with simple fractions and gradually increase complexity. Focus on understanding the concepts rather than memorization.
Conclusion
Determining whether 1/4 is bigger than 5/8 is a simple yet illustrative example of comparing fractions. The answer is unequivocally no; 5/8 is significantly larger than 1/4. However, the value of this exercise extends far beyond the immediate answer. By mastering the methods of comparing fractions – finding a common denominator, converting to decimals, or using visual representations – you build a strong foundation in mathematics, fostering problem-solving skills applicable across various disciplines and real-world scenarios. Remember, understanding the underlying principles is far more valuable than just knowing the answer to a single problem. Continue to practice and explore different methods to solidify your grasp of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
1 4 Of 3 4
Sep 13, 2025
-
Is 5 6 Greater Than 2 3
Sep 13, 2025
-
What Is 30 Off 49 99
Sep 13, 2025
-
Is 4 5 Less Than 1 2
Sep 13, 2025
-
What Is 30 Off 30
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Bigger Than 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.