Is 1/4 Greater Than 1/5
saludintensiva
Sep 14, 2025 · 5 min read
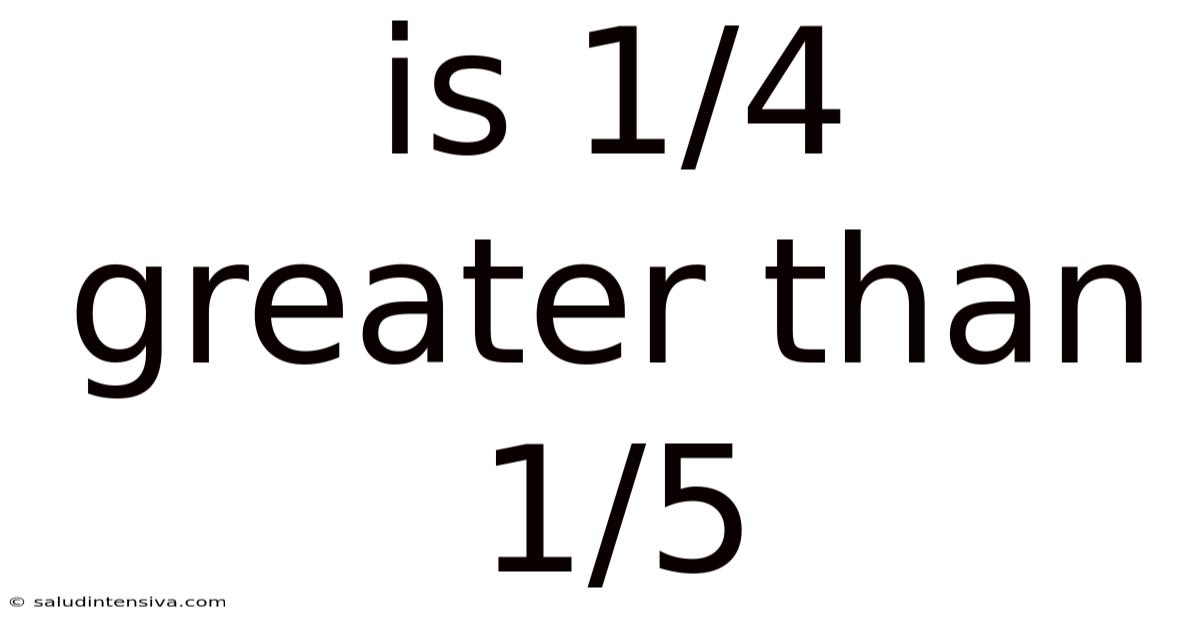
Table of Contents
Is 1/4 Greater Than 1/5? A Deep Dive into Fraction Comparison
Understanding fractions is a cornerstone of mathematical literacy. This article will explore the seemingly simple question, "Is 1/4 greater than 1/5?", providing a comprehensive explanation accessible to all, from elementary school students to those brushing up on their math skills. We will delve into various methods for comparing fractions, examining their underlying principles and providing practical examples to solidify your understanding. This will involve visual representations, numerical comparisons, and a discussion of the concepts of numerators and denominators. By the end, you'll not only know the answer to the initial question but also possess the tools to confidently compare any two fractions.
Introduction: Understanding Fractions
Before diving into the comparison, let's establish a solid foundation in understanding fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) signifies that the whole is divided into four equal parts. Similarly, 1/5 represents one part out of five equal parts.
Visual Comparison: The Pizza Analogy
One of the easiest ways to compare fractions is through visualization. Imagine two pizzas, both of the same size.
- Pizza 1: Cut into four equal slices (representing 1/4).
- Pizza 2: Cut into five equal slices (representing 1/5).
If you take one slice from each pizza, which slice is larger? The slice from Pizza 1 (1/4) is visibly larger than the slice from Pizza 2 (1/5). This simple visual representation demonstrates that 1/4 is greater than 1/5.
Numerical Comparison: Finding a Common Denominator
While visual comparisons are helpful, a more robust method involves finding a common denominator. This means finding a number that is a multiple of both denominators (4 and 5). The least common multiple (LCM) of 4 and 5 is 20.
To express both fractions with a denominator of 20, we perform the following calculations:
- 1/4: Multiply both the numerator and the denominator by 5: (1 x 5) / (4 x 5) = 5/20
- 1/5: Multiply both the numerator and the denominator by 4: (1 x 4) / (5 x 4) = 4/20
Now, comparing 5/20 and 4/20 is straightforward. Since 5 is greater than 4, we conclude that 5/20 (or 1/4) is greater than 4/20 (or 1/5).
Decimal Conversion: Expressing Fractions as Decimals
Another effective method is converting the fractions into decimals. This involves dividing the numerator by the denominator:
- 1/4: 1 ÷ 4 = 0.25
- 1/5: 1 ÷ 5 = 0.20
Comparing the decimal values, 0.25 is clearly greater than 0.20, confirming that 1/4 is greater than 1/5. This method is particularly useful when dealing with more complex fractions or when you need to perform calculations involving fractions and decimals.
The Importance of the Denominator: A Deeper Look
The denominator plays a crucial role in determining the size of a fraction. A smaller denominator indicates that the whole is divided into fewer parts, making each part larger. Conversely, a larger denominator signifies more parts, resulting in smaller individual parts.
Consider the following examples:
- 1/2: One out of two equal parts – a relatively large portion.
- 1/10: One out of ten equal parts – a much smaller portion.
This inverse relationship between the denominator and the size of the fraction is fundamental to understanding fraction comparisons.
Comparing Fractions with Different Numerators and Denominators
The methods discussed above can be extended to compare fractions with different numerators and denominators. Let's compare 3/8 and 5/12:
Method 1: Finding a Common Denominator
The least common multiple of 8 and 12 is 24.
- 3/8: (3 x 3) / (8 x 3) = 9/24
- 5/12: (5 x 2) / (12 x 2) = 10/24
Since 10/24 > 9/24, we conclude that 5/12 > 3/8.
Method 2: Decimal Conversion
- 3/8: 3 ÷ 8 = 0.375
- 5/12: 5 ÷ 12 = 0.41666...
Again, 0.41666... > 0.375, confirming that 5/12 > 3/8.
Cross-Multiplication: A Shortcut for Comparison
For comparing two fractions, cross-multiplication offers a convenient shortcut. To compare a/b and c/d, we cross-multiply:
- If (a x d) > (b x c), then a/b > c/d
- If (a x d) < (b x c), then a/b < c/d
- If (a x d) = (b x c), then a/b = c/d
Let's apply this to our original problem:
- 1/4 and 1/5
- (1 x 5) = 5
- (4 x 1) = 4
- Since 5 > 4, 1/4 > 1/5
This method provides a quick and efficient way to compare fractions without the need to find a common denominator.
Frequently Asked Questions (FAQs)
Q: Are there any other ways to compare fractions besides the ones mentioned?
A: Yes, there are other methods, but they often build upon the principles explained above. For instance, you can convert fractions to percentages before comparing them. However, the methods discussed provide a comprehensive and accessible approach.
Q: What if the fractions are negative?
A: When comparing negative fractions, the rules are reversed. The fraction with the smaller absolute value (the distance from zero) will be greater. For example, -1/4 > -1/5 because -1/4 is closer to zero.
Q: How can I teach these concepts to young children?
A: Using visual aids like fraction circles, pizza slices, or even blocks is highly effective. Relate the fractions to real-life situations they understand. Start with simple fractions and gradually increase the complexity.
Conclusion: Mastering Fraction Comparison
Understanding how to compare fractions is a crucial skill in mathematics. This article has explored various methods – visual representations, common denominators, decimal conversions, and cross-multiplication – providing a comprehensive approach to tackle fraction comparisons. Remember, a smaller denominator implies larger portions, and using a common denominator or converting to decimals allows for a direct numerical comparison. Mastering these techniques will significantly enhance your mathematical abilities and confidence when dealing with fractions in any context. By understanding the underlying principles and practicing different methods, you’ll be able to confidently tackle any fraction comparison problem. Remember to choose the method that works best for you and the specific problem you're trying to solve. Practice makes perfect, so keep practicing until you feel comfortable with these essential skills.
Latest Posts
Latest Posts
-
Grams Cm3 To Lbs Ft3
Sep 14, 2025
-
10 15 Is Equivalent To
Sep 14, 2025
-
3 50 As A Decimal
Sep 14, 2025
-
What Is 7 Degrees C
Sep 14, 2025
-
Surface Area Formula Calc 2
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 Greater Than 1/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.