Is 1/6 Equal To 1/3
saludintensiva
Sep 12, 2025 · 6 min read
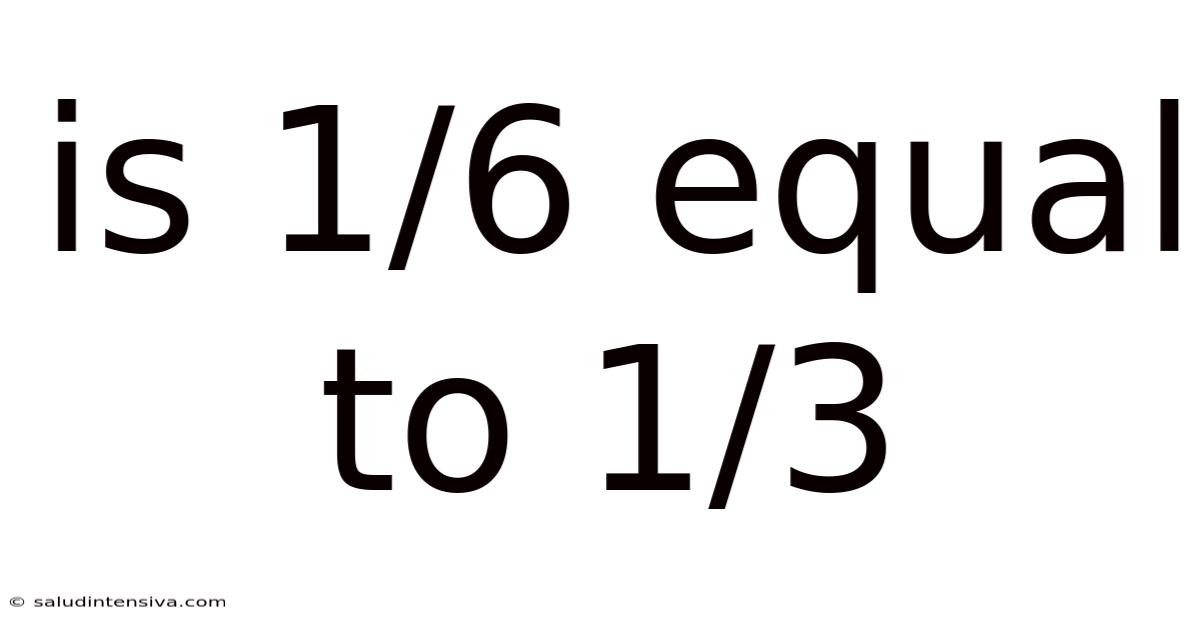
Table of Contents
Is 1/6 Equal to 1/3? Understanding Fractions and Equivalence
Are you struggling with fractions? Many people find fractions confusing, and a common question that arises is: Is 1/6 equal to 1/3? The short answer is no, but understanding why requires a deeper look at the fundamental concepts of fractions and their equivalence. This article will explore the world of fractions, explain why 1/6 and 1/3 are not equal, and provide you with the tools to confidently compare and manipulate fractions.
Understanding Fractions: Parts of a Whole
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells you how many equal parts the whole is divided into, while the numerator tells you how many of those parts you have. For example, in the fraction 1/6, the denominator (6) means the whole is divided into six equal parts, and the numerator (1) means you have one of those parts. Similarly, 1/3 means the whole is divided into three equal parts, and you have one of them.
Visualizing Fractions: The Power of Representation
Let's visualize these fractions using simple diagrams. Imagine a pizza cut into six equal slices. 1/6 represents one of those six slices. Now, imagine a different pizza cut into only three equal slices. 1/3 represents one of those three slices. Can you see the difference? One slice from a six-slice pizza is clearly smaller than one slice from a three-slice pizza. This visual representation immediately shows that 1/6 is not the same size as 1/3.
Comparing Fractions: Finding Common Ground
To compare fractions directly, we need to find a common denominator. This means finding a number that is a multiple of both denominators. In our case, the denominators are 6 and 3. The least common multiple (LCM) of 6 and 3 is 6. We can convert 1/3 to an equivalent fraction with a denominator of 6.
To do this, we ask ourselves: "What do we multiply 3 by to get 6?" The answer is 2. Whatever we do to the denominator, we must do to the numerator to keep the fraction equivalent. So, we multiply both the numerator and the denominator of 1/3 by 2:
(1 * 2) / (3 * 2) = 2/6
Now we can compare 1/6 and 2/6. Clearly, 2/6 is larger than 1/6. Therefore, 1/3 (which is equivalent to 2/6) is not equal to 1/6.
The Importance of Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they look different. They are essentially different ways of expressing the same part of a whole. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. They all represent half of a whole. Understanding equivalent fractions is crucial for comparing and performing operations (addition, subtraction, multiplication, and division) with fractions.
To find equivalent fractions, you simply multiply or divide both the numerator and the denominator by the same non-zero number. This maintains the ratio and thus the value of the fraction.
Simplifying Fractions: Finding the Lowest Terms
Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and compare. For example, the fraction 6/12 can be simplified by dividing both the numerator and denominator by their greatest common factor (GCF), which is 6:
6/12 = (6 ÷ 6) / (12 ÷ 6) = 1/2
Adding and Subtracting Fractions: A Common Denominator is Key
When adding or subtracting fractions, you must have a common denominator. If the fractions don't have a common denominator, you must first convert them to equivalent fractions with the same denominator. Let's illustrate with an example:
1/3 + 1/6
First, find a common denominator (6). Convert 1/3 to an equivalent fraction with a denominator of 6 (2/6). Now, we can add:
2/6 + 1/6 = 3/6
This fraction can be simplified to 1/2.
Multiplying Fractions: A Simpler Approach
Multiplying fractions is simpler than adding or subtracting them. You simply multiply the numerators together and the denominators together:
(1/3) * (1/6) = (1 * 1) / (3 * 6) = 1/18
Dividing Fractions: Inverting and Multiplying
Dividing fractions involves inverting (flipping) the second fraction and then multiplying:
(1/3) ÷ (1/6) = (1/3) * (6/1) = 6/3 = 2
Practical Applications of Fractions
Fractions are essential in many areas of life, including:
- Cooking and Baking: Recipes often use fractions to specify ingredient amounts.
- Construction and Engineering: Precise measurements and calculations frequently involve fractions.
- Finance: Calculating percentages, interest rates, and proportions often rely on fractions.
- Science: Many scientific measurements and ratios are expressed as fractions.
Frequently Asked Questions (FAQ)
Q: How can I easily determine if two fractions are equal?
A: Simplify both fractions to their lowest terms. If they are identical after simplification, then they are equal. Alternatively, find a common denominator and compare the numerators.
Q: What is the difference between a proper fraction and an improper fraction?
A: A proper fraction has a numerator smaller than its denominator (e.g., 1/3, 2/5). An improper fraction has a numerator equal to or larger than its denominator (e.g., 5/3, 8/8). Improper fractions can be expressed as mixed numbers (a whole number and a proper fraction).
Q: How do I convert an improper fraction to a mixed number?
A: Divide the numerator by the denominator. The quotient is the whole number part of the mixed number, and the remainder is the numerator of the proper fraction part, with the original denominator remaining the same. For example, 7/3 = 2 1/3.
Q: Why is understanding fractions important?
A: Fractions are fundamental to mathematics and have widespread applications in everyday life, from cooking to finance to scientific research. A strong understanding of fractions builds a solid foundation for more advanced mathematical concepts.
Conclusion: Mastering Fractions for a Brighter Future
In summary, 1/6 is definitively not equal to 1/3. Understanding the concepts of fractions, equivalent fractions, and common denominators is essential for correctly comparing and manipulating fractions. By mastering these fundamentals, you will build confidence in your mathematical abilities and unlock a deeper understanding of the world around you. Fractions might seem daunting at first, but with practice and a clear understanding of the underlying principles, you can conquer them and appreciate their power and importance. Remember the visual representations, practice regularly, and don't hesitate to explore different methods and approaches until you find the one that resonates best with your learning style. The journey to mastering fractions is rewarding, leading to a stronger foundation in mathematics and a greater ability to tackle complex problems.
Latest Posts
Latest Posts
-
How To Multiply 100 Percent
Sep 12, 2025
-
What Is 1 2 8
Sep 12, 2025
-
7 10 As A Percent
Sep 12, 2025
-
Gcf Of 72 And 36
Sep 12, 2025
-
17 50 As A Decimal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 1/6 Equal To 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.