Is 2/3 Greater Than 2/8
saludintensiva
Sep 18, 2025 · 5 min read
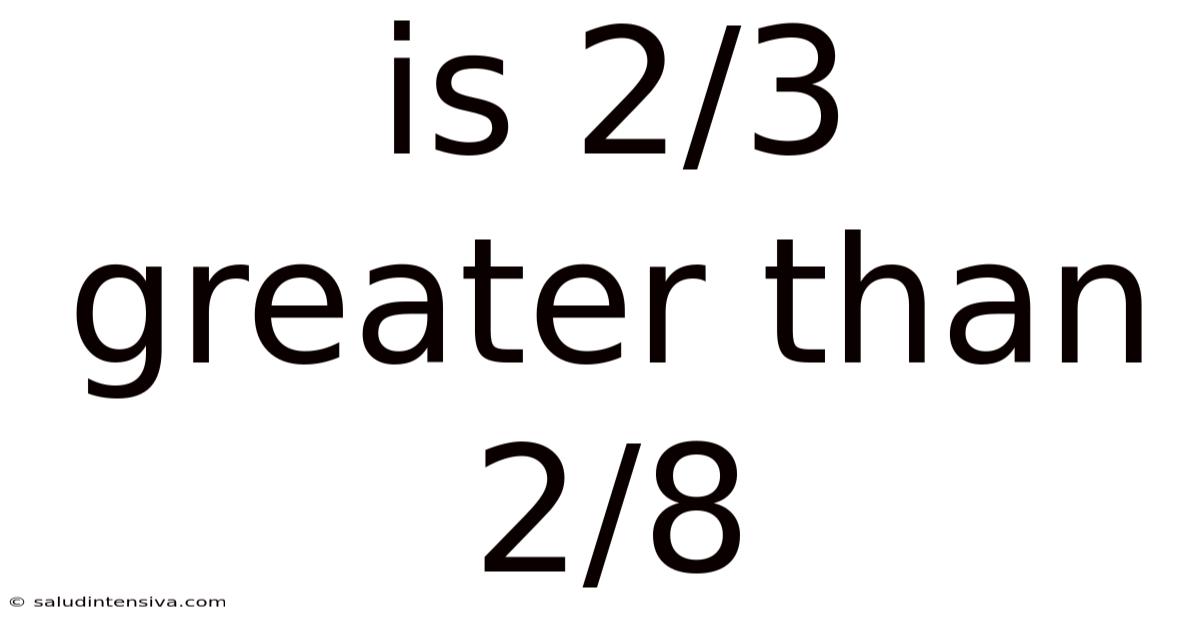
Table of Contents
Is 2/3 Greater Than 2/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will not only answer the question, "Is 2/3 greater than 2/8?" but also provide a comprehensive exploration of fraction comparison techniques, ensuring you gain a solid grasp of this concept. We'll delve into various methods, from visual representations to numerical calculations, equipping you with the tools to confidently compare any two fractions.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 2/3, the denominator (3) means the whole is divided into three equal parts, and the numerator (2) indicates we're looking at two of those parts.
Comparing 2/3 and 2/8: A Visual Approach
Let's start with a simple visual comparison. Imagine two identical pizzas. We'll divide the first pizza into three equal slices and take two slices (representing 2/3). We'll divide the second pizza into eight equal slices and take two slices (representing 2/8). Looking at the two pizzas, it's immediately apparent that two slices out of three represent a larger portion than two slices out of eight. Therefore, 2/3 is greater than 2/8.
Comparing 2/3 and 2/8: Numerical Methods
While visual representations are helpful for understanding, numerical methods are necessary for more complex fraction comparisons. Several techniques can be employed:
-
Comparing Numerators with Equal Denominators: This method works best when the numerators are the same. In such cases, the fraction with the smaller denominator represents the larger value. For example, 1/2 > 1/4 because halving something gives you a larger piece than quartering it. However, this method isn't directly applicable to comparing 2/3 and 2/8 because their numerators are the same but their denominators are different.
-
Finding a Common Denominator: This is the most versatile and reliable method for comparing fractions with different denominators. The key is to find a common multiple of both denominators (a number that both denominators divide into evenly). The least common multiple (LCM) is the smallest such number, making calculations simpler.
To compare 2/3 and 2/8, we need to find the LCM of 3 and 8. The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24... The multiples of 8 are 8, 16, 24... The LCM of 3 and 8 is 24.
Now we convert both fractions to have a denominator of 24:
-
2/3: To get a denominator of 24, we multiply both the numerator and the denominator by 8 (24/3 = 8): (2 * 8) / (3 * 8) = 16/24
-
2/8: To get a denominator of 24, we multiply both the numerator and the denominator by 3 (24/8 = 3): (2 * 3) / (8 * 3) = 6/24
Now we can easily compare 16/24 and 6/24. Since 16 > 6, we conclude that 16/24 (or 2/3) is greater than 6/24 (or 2/8).
-
Converting to Decimals: Another approach involves converting fractions to decimals. To do this, simply divide the numerator by the denominator:
-
2/3 ≈ 0.667
-
2/8 = 0.25
Since 0.667 > 0.25, we confirm that 2/3 is greater than 2/8.
Understanding the Relationship Between Numerator and Denominator
The size of a fraction is determined by the relationship between its numerator and denominator. When the numerator is significantly smaller than the denominator, the fraction represents a small part of the whole (e.g., 1/10). Conversely, when the numerator is close to the denominator, the fraction represents a large part of the whole (e.g., 9/10). This intuitive understanding is crucial for quickly estimating the relative sizes of fractions.
In the case of 2/3 and 2/8, although both have the same numerator (2), the denominator significantly affects the value. The smaller denominator (3) results in a larger fraction because the whole is divided into fewer parts, making each part larger.
Extending the Concept: Comparing Fractions with Different Numerators and Denominators
The methods described above—finding a common denominator and converting to decimals—are equally effective for comparing fractions with different numerators and denominators. Let's take an example: compare 3/4 and 5/6.
-
Finding a Common Denominator: The LCM of 4 and 6 is 12.
-
3/4 = (3 * 3) / (4 * 3) = 9/12
-
5/6 = (5 * 2) / (6 * 2) = 10/12
Since 10/12 > 9/12, we conclude that 5/6 > 3/4.
-
Converting to Decimals:
-
3/4 = 0.75
-
5/6 ≈ 0.833
Again, we confirm that 5/6 > 3/4.
Frequently Asked Questions (FAQ)
-
Q: Is there a quick way to compare fractions without using calculations?
- A: While not always foolproof, a quick estimate can sometimes be made by observing the relative sizes of the numerators and denominators. If the numerator is a large portion of the denominator (e.g., close to half or more), the fraction is likely to be larger. However, this method is less reliable than finding a common denominator or converting to decimals.
-
Q: What if the fractions are improper fractions (where the numerator is greater than the denominator)?
- A: The same methods (finding a common denominator or converting to decimals) apply to improper fractions. Remember that improper fractions are greater than 1.
-
Q: How can I improve my understanding of fractions?
- A: Practice is key! Solve numerous fraction comparison problems, using various methods to solidify your understanding. Visual aids, like diagrams and manipulatives, can also be helpful, especially for beginners.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a vital skill that forms the foundation for many mathematical concepts. This article has provided a thorough examination of several methods for comparing fractions, from the intuitive visual approach to the more precise numerical methods of finding a common denominator and converting to decimals. By mastering these techniques, you'll gain confidence in tackling fraction-related problems and will be well-equipped to handle more advanced mathematical concepts. Remember, consistent practice is the key to achieving proficiency in fraction comparison and mastering this fundamental aspect of mathematics. Understanding the relationship between the numerator and denominator, and choosing the most appropriate method for the problem at hand, are essential steps towards achieving mathematical fluency.
Latest Posts
Latest Posts
-
Write 1 4 As A Percent
Sep 18, 2025
-
20 4 In Decimal Form
Sep 18, 2025
-
19 4 As A Decimal
Sep 18, 2025
-
4 To The 3rd Power
Sep 18, 2025
-
Convert 175 C To Fahrenheit
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Greater Than 2/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.