Is 2/3 More Than 3/4
saludintensiva
Sep 18, 2025 · 5 min read
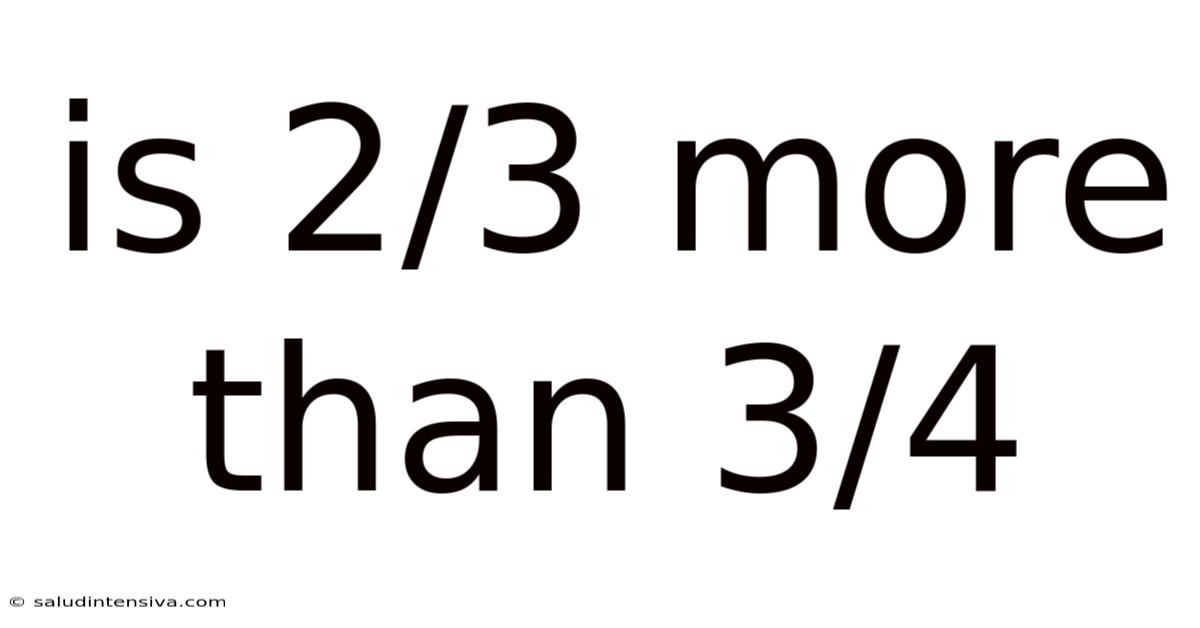
Table of Contents
Is 2/3 More Than 3/4? Deconstructing Fractions and Mastering Comparisons
Are you struggling with comparing fractions? Many find comparing fractions like 2/3 and 3/4 challenging, but mastering this skill is crucial for success in mathematics and beyond. This comprehensive guide will not only answer the question "Is 2/3 more than 3/4?" but will also equip you with the tools and understanding to confidently compare any two fractions. We'll explore various methods, from visual representations to numerical calculations, ensuring a deep understanding of the underlying concepts.
Understanding Fractions: A Foundation for Comparison
Before diving into the comparison of 2/3 and 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator (2) indicates we have two parts, and the denominator (3) indicates the whole is divided into three equal parts.
Method 1: Visual Representation – The Power of Pictures
One of the most intuitive ways to compare fractions is through visual representations. Let's use a simple diagram to compare 2/3 and 3/4.
Imagine two identical rectangles. Divide the first rectangle into three equal parts and shade two of them to represent 2/3. Divide the second rectangle into four equal parts and shade three of them to represent 3/4.
By visually comparing the shaded areas, it becomes clear that the shaded area representing 3/4 is larger than the shaded area representing 2/3. Therefore, 3/4 is greater than 2/3.
Method 2: Finding a Common Denominator – The Numerical Approach
Visual representations are helpful, but for more complex fractions, a numerical approach is necessary. This involves finding a common denominator, a number that is a multiple of both denominators.
-
Identify the denominators: In our case, the denominators are 3 and 4.
-
Find the least common multiple (LCM): The LCM of 3 and 4 is 12 (because 3 x 4 = 12 and 12 is the smallest number divisible by both 3 and 4).
-
Convert the fractions to equivalent fractions with the common denominator:
-
To convert 2/3 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
To convert 3/4 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
-
-
Compare the numerators: Now that both fractions have the same denominator, we can compare their numerators. Since 9 > 8, we conclude that 9/12 (or 3/4) is greater than 8/12 (or 2/3).
Therefore, 3/4 is greater than 2/3.
Method 3: Converting to Decimals – A Familiar Format
Another approach involves converting the fractions to decimals. This method leverages our familiarity with decimal numbers and simplifies the comparison process.
-
Divide the numerator by the denominator for each fraction:
- 2/3 = 0.666... (a repeating decimal)
- 3/4 = 0.75
-
Compare the decimal values: Since 0.75 > 0.666..., we conclude that 3/4 is greater than 2/3.
Method 4: Cross-Multiplication – A Quick Comparison Technique
Cross-multiplication offers a swift method for comparing fractions, especially when finding a common denominator seems cumbersome.
-
Cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction (2) by the denominator of the second fraction (4): 2 x 4 = 8
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (3): 3 x 3 = 9
-
Compare the products: Since 9 > 8, we conclude that 3/4 is greater than 2/3.
Beyond the Comparison: Understanding the Magnitude of the Difference
While we've established that 3/4 is greater than 2/3, it's also insightful to understand the magnitude of this difference. We can calculate the difference between the two fractions:
3/4 - 2/3 = (9/12) - (8/12) = 1/12
This means 3/4 is 1/12 larger than 2/3. This seemingly small difference highlights the precision offered by fractional comparisons.
Addressing Common Misconceptions
Many students fall into the trap of comparing numerators or denominators individually without considering the relationship between them. It's crucial to remember that comparing fractions requires considering both the numerator and the denominator. Simply saying "3 is bigger than 2, therefore 3/4 is bigger than 2/3" is incorrect.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to compare fractions?
A: Yes, calculators can be helpful, especially for converting fractions to decimals. However, understanding the underlying principles of fraction comparison is vital for developing a solid mathematical foundation.
Q: Are there other methods for comparing fractions besides these four?
A: Yes, there are other techniques, some more advanced, including using fraction bars and number lines. The methods presented here provide a strong starting point.
Q: What if I have more than two fractions to compare?
A: You can extend any of the methods discussed to compare multiple fractions. For instance, you can convert all fractions to equivalent fractions with a common denominator and then compare their numerators.
Q: Why is understanding fraction comparison important?
A: Fraction comparison is fundamental to numerous mathematical concepts, including ratios, proportions, and percentages. A strong grasp of this concept forms the foundation for advanced mathematical problem-solving.
Conclusion: Mastering Fractions for a Brighter Future
Comparing fractions, such as determining whether 2/3 is more than 3/4, might initially seem daunting. However, by utilizing the methods discussed – visual representation, common denominators, decimal conversion, and cross-multiplication – you can confidently navigate the world of fractions. Understanding the underlying principles allows you not only to solve specific problems but also to develop a deeper mathematical intuition that will serve you well in future studies and applications. Remember, practice is key. The more you work with fractions, the more comfortable and proficient you will become. So, grab a pencil and paper, and start practicing! You've got this!
Latest Posts
Latest Posts
-
3 8 Minus 1 4
Sep 18, 2025
-
2 3 4 To Improper Fraction
Sep 18, 2025
-
18 Percent In Decimal Form
Sep 18, 2025
-
Gcf Of 5 And 8
Sep 18, 2025
-
What Is 43 In Celsius
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 More Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.