Is 2/5 Equal To 4/10
saludintensiva
Sep 16, 2025 · 6 min read
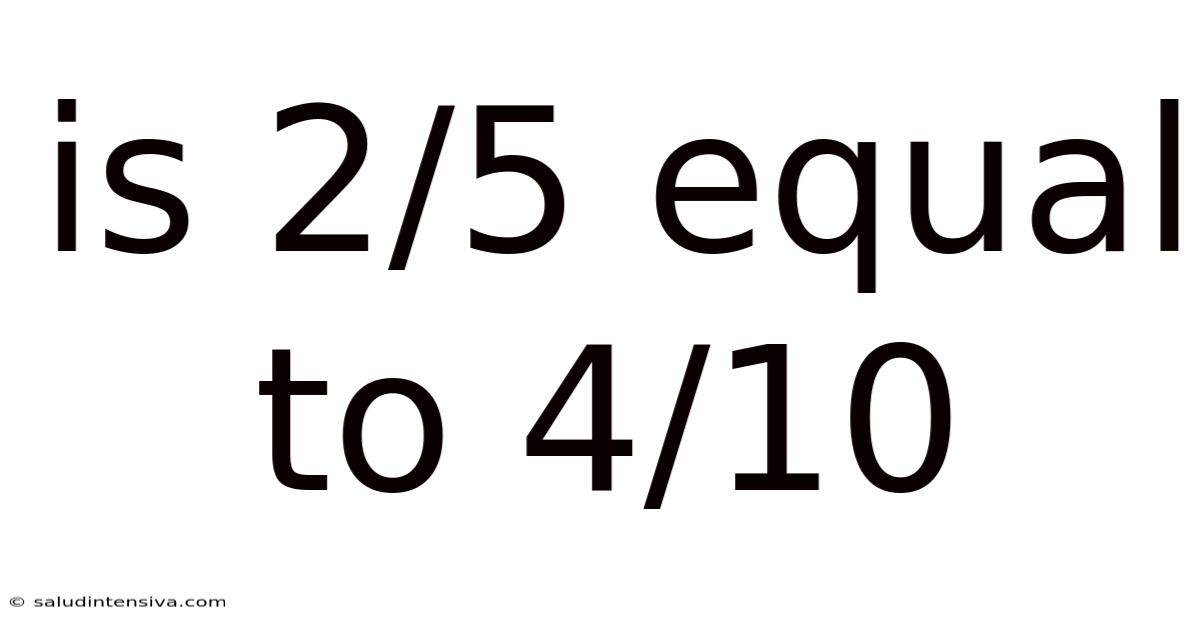
Table of Contents
Is 2/5 Equal to 4/10? A Deep Dive into Equivalent Fractions
Are you grappling with fractions? Understanding equivalent fractions is a fundamental concept in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This article will explore the question: Is 2/5 equal to 4/10? We'll delve into the mathematical principles behind equivalent fractions, provide practical examples, and even explore the broader implications of this concept in various fields. By the end, you'll not only know the answer but also understand why it's true and how to identify other equivalent fractions with confidence.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's briefly review what a fraction represents. A fraction, such as 2/5, is a way of expressing a part of a whole. The number on top, the numerator, represents the number of parts we have. The number on the bottom, the denominator, represents the total number of equal parts the whole is divided into.
So, 2/5 means we have 2 parts out of a total of 5 equal parts. Visualize a pizza cut into 5 slices; 2/5 represents having 2 of those slices.
Exploring the Equality: Is 2/5 Equal to 4/10?
Yes, 2/5 is equal to 4/10. These are equivalent fractions. But what does that mean exactly? Equivalent fractions represent the same proportion or value, even though they look different.
Think back to our pizza example. Imagine now we cut the same pizza into 10 slices instead of 5. If you have 4 out of those 10 slices (4/10), you still have the same amount of pizza as if you had 2 out of 5 slices (2/5). The proportion remains unchanged.
The Mathematical Proof: Multiplying and Dividing Fractions
The key to understanding equivalent fractions lies in the concept of multiplying or dividing both the numerator and the denominator by the same number. This operation doesn't change the value of the fraction, only its representation.
Let's demonstrate with our example:
-
To show that 2/5 is equal to 4/10: We can multiply both the numerator and denominator of 2/5 by 2:
(2 x 2) / (5 x 2) = 4/10
-
To show that 4/10 is equal to 2/5: We can divide both the numerator and denominator of 4/10 by 2:
(4 ÷ 2) / (10 ÷ 2) = 2/5
This process works for any equivalent fraction. You can multiply or divide by any non-zero number. Multiplying increases the size of the numerator and denominator proportionally, while dividing reduces them proportionally. The crucial point is that the ratio between the numerator and the denominator remains constant.
Visual Representation: Understanding Equivalence Through Diagrams
Visual aids can significantly enhance understanding. Let's use diagrams to illustrate the equivalence of 2/5 and 4/10:
Imagine two identical rectangles.
-
Rectangle 1: Divide it into 5 equal parts and shade 2 of them. This represents 2/5.
-
Rectangle 2: Divide it into 10 equal parts and shade 4 of them. This represents 4/10.
Observe that the shaded area in both rectangles is visually identical, even though the number of parts and shaded parts differ. This visual confirmation reinforces the mathematical proof that 2/5 and 4/10 are equivalent fractions.
Simplifying Fractions: Finding the Lowest Terms
The process of dividing both the numerator and the denominator by their greatest common divisor (GCD) is called simplifying or reducing a fraction to its lowest terms. This gives us the simplest form of a fraction while maintaining its value.
In our example, the GCD of 4 and 10 is 2. Dividing both by 2 gives us 2/5, the simplified form of 4/10. A fraction in its lowest terms is considered the most efficient representation.
Applications of Equivalent Fractions in Real Life
Equivalent fractions are not just an abstract mathematical concept; they have practical applications across numerous fields:
-
Cooking and Baking: Recipes often use fractions. Understanding equivalent fractions allows you to adjust recipes based on the ingredients you have available. For example, if a recipe calls for 1/2 cup of sugar, and you only have a 1/4 cup measuring cup, you know you need two 1/4 cups.
-
Construction and Engineering: Accurate measurements are crucial. Equivalent fractions help in converting measurements from one unit to another (e.g., inches to feet) or ensuring proportions are maintained in blueprints and designs.
-
Finance and Economics: Dealing with percentages and proportions is fundamental in finance. Understanding equivalent fractions aids in comparing different financial instruments or interpreting financial data.
-
Data Analysis and Statistics: Representing and interpreting data often involves fractions and proportions. Equivalent fractions assist in simplifying and comparing data sets.
-
Science and Measurement: In scientific experiments and measurements, equivalent fractions can help in scaling data or converting units.
Beyond 2/5 and 4/10: Identifying Other Equivalent Fractions
The principles we've discussed apply to any fraction. To find equivalent fractions for any given fraction:
-
Identify the given fraction. For example, let's use 3/4.
-
Multiply or divide both the numerator and the denominator by the same non-zero number.
- Multiplying by 2: (3 x 2) / (4 x 2) = 6/8
- Multiplying by 3: (3 x 3) / (4 x 3) = 9/12
- Multiplying by 4: (3 x 4) / (4 x 4) = 12/16
- And so on...
You can also divide if the numerator and denominator are divisible by a common factor.
Frequently Asked Questions (FAQ)
Q1: Can I multiply the numerator and denominator by different numbers to find an equivalent fraction?
A1: No. Multiplying the numerator and denominator by different numbers will change the value of the fraction. The ratio must remain constant for the fractions to be equivalent.
Q2: Is there a limit to the number of equivalent fractions a given fraction can have?
A2: No. There are infinitely many equivalent fractions for any given fraction. You can continue multiplying the numerator and denominator by any number infinitely.
Q3: How do I know if two fractions are equivalent without performing calculations?
A3: You can cross-multiply. If the product of the numerator of one fraction and the denominator of the other is equal to the product of the numerator of the second fraction and the denominator of the first, the fractions are equivalent. For example: Is 2/5 = 4/10? (2 x 10) = 20 and (5 x 4) = 20. Since they are equal, the fractions are equivalent.
Q4: Why is simplifying fractions important?
A4: Simplifying fractions makes them easier to work with and understand. It provides a clear and concise representation of the value. It’s also essential for comparing fractions effectively.
Conclusion: Mastering the Fundamentals of Equivalent Fractions
Understanding equivalent fractions is a cornerstone of mathematical literacy. We've established definitively that 2/5 is indeed equal to 4/10. We've explored the underlying mathematical principles, illustrated the concept visually, and examined its practical applications in various aspects of life. By grasping the concept of multiplying or dividing both the numerator and denominator by the same number, you can confidently identify and work with equivalent fractions, opening doors to a deeper understanding of mathematical concepts and their real-world implications. Remember, the journey to mastering mathematics is a process of building a solid foundation, one concept at a time. This understanding of equivalent fractions is an important step in that journey.
Latest Posts
Latest Posts
-
Gcf Of 27 And 30
Sep 17, 2025
-
Capacity Of A Gas Tank
Sep 17, 2025
-
Gcf Of 17 And 34
Sep 17, 2025
-
16 3 As A Fraction
Sep 17, 2025
-
Whats 15 Kg In Pounds
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Equal To 4/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.