Is 2/5 Greater Than 3/5
saludintensiva
Sep 14, 2025 · 5 min read
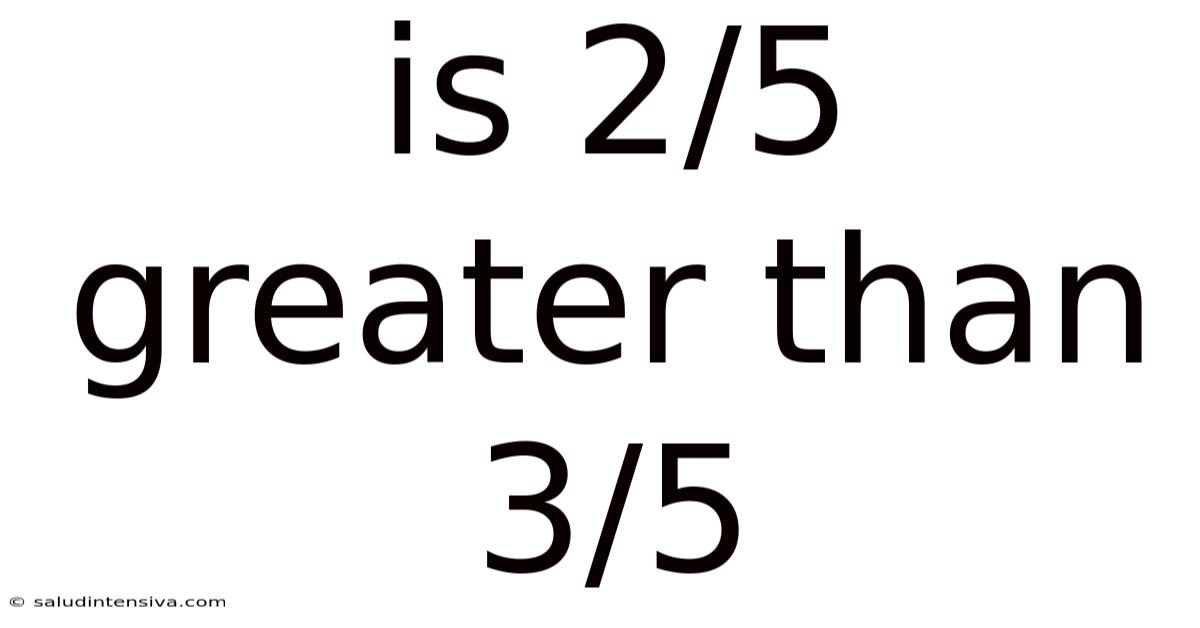
Table of Contents
Is 2/5 Greater Than 3/5? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental concept in mathematics, crucial for everyday life and advanced studies alike. This article will thoroughly explore the question, "Is 2/5 greater than 3/5?", providing not just the answer but a comprehensive understanding of fraction comparison, including various methods and their applications. We'll delve into the underlying principles, offering practical examples and addressing frequently asked questions to solidify your grasp of this essential mathematical skill.
Introduction: Understanding Fractions
Before tackling the core question, let's establish a solid understanding of fractions. A fraction represents a part of a whole. It's composed of two key components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For instance, in the fraction 2/5, the numerator is 2, and the denominator is 5. This means we have 2 out of 5 equal parts of a whole.
Comparing Fractions: The Core Concept
Comparing fractions involves determining which fraction represents a larger or smaller portion of a whole. Several methods can be used, each with its advantages and disadvantages. Let's explore the most common approaches:
1. Common Denominator Method
This is the most straightforward and widely used method for comparing fractions. The principle is to convert the fractions into equivalent fractions with the same denominator. Once the denominators are identical, we can directly compare the numerators. The fraction with the larger numerator represents the greater value.
Let's apply this method to our question: Is 2/5 greater than 3/5?
Both fractions already have the same denominator (5). Therefore, we can directly compare the numerators: 2 and 3. Since 3 > 2, we conclude that 3/5 is greater than 2/5.
2. Visual Representation: Using Fraction Bars or Circles
Visual aids can significantly enhance understanding, especially for beginners. Imagine a rectangle or circle divided into five equal parts. Shade two parts to represent 2/5 and three parts to represent 3/5. Visually, it becomes immediately apparent that 3/5 covers a larger area, confirming that 3/5 > 2/5.
This method is particularly helpful for developing an intuitive understanding of fraction magnitudes.
3. Converting to Decimals
Another effective method is to convert the fractions into their decimal equivalents. This involves dividing the numerator by the denominator.
- 2/5 = 2 ÷ 5 = 0.4
- 3/5 = 3 ÷ 5 = 0.6
Comparing the decimal equivalents, 0.6 > 0.4, thus confirming that 3/5 is greater than 2/5. This method offers a clear numerical comparison, particularly useful when dealing with more complex fractions.
4. Cross-Multiplication
Cross-multiplication is a powerful technique for comparing two fractions. It involves multiplying the numerator of one fraction by the denominator of the other and vice-versa. The fraction with the larger product is the greater fraction.
Let's compare 2/5 and 3/5 using this method:
- 2 * 5 = 10
- 3 * 5 = 15
Since 15 > 10, 3/5 is greater than 2/5. This method is particularly efficient when dealing with fractions that don't share a common denominator.
Illustrative Examples: Extending the Concept
Let's expand our understanding with more complex examples:
Example 1: Compare 2/3 and 4/5.
Using the common denominator method:
- The least common multiple (LCM) of 3 and 5 is 15.
- 2/3 = (2 * 5) / (3 * 5) = 10/15
- 4/5 = (4 * 3) / (5 * 3) = 12/15
- Since 12 > 10, 4/5 > 2/3.
Example 2: Compare 7/8 and 5/6.
Using cross-multiplication:
- 7 * 6 = 42
- 5 * 8 = 40
- Since 42 > 40, 7/8 > 5/6.
The Importance of Understanding Fraction Comparison
Mastering fraction comparison is essential for several reasons:
- Everyday Applications: From cooking and baking (measuring ingredients) to calculating discounts and understanding proportions, fractions are ubiquitous in our daily lives.
- Academic Success: A strong understanding of fractions is fundamental for progressing in mathematics, science, and other related fields. It forms the basis for more advanced concepts like algebra, geometry, and calculus.
- Problem-Solving Skills: Comparing fractions helps develop critical thinking and problem-solving skills, which are valuable assets in various aspects of life.
Frequently Asked Questions (FAQ)
Q1: Why is the common denominator method so important?
A1: The common denominator method allows for a direct comparison of numerators. Having the same denominator ensures that we are comparing like quantities – parts of the same whole.
Q2: Can I always find a common denominator?
A2: Yes, you can always find a common denominator for any two (or more) fractions. The least common multiple (LCM) of the denominators serves as the common denominator.
Q3: Which method is the best for comparing fractions?
A3: There's no single "best" method. The most suitable approach depends on the specific fractions involved and your comfort level with different techniques. Visual representation is great for understanding, while cross-multiplication can be efficient for more complex fractions. The common denominator method provides a foundational approach and works well for most comparisons.
Q4: What if the fractions have different denominators and numerators?
A4: If the fractions have different denominators and numerators, you'll need to employ one of the methods mentioned above (common denominator, decimals, or cross-multiplication) to compare them effectively.
Conclusion: Reinforcing the Understanding
We've definitively answered the initial question: 2/5 is not greater than 3/5; 3/5 is greater than 2/5. However, the value of this article extends far beyond a simple answer. We've explored various methods for comparing fractions, highlighting their strengths and applications. By mastering these techniques and understanding the underlying principles, you'll develop a robust foundation for tackling more complex mathematical concepts and confidently navigate the world of fractions in all aspects of your life. Remember to practice regularly, using different methods and examples to reinforce your understanding. With consistent effort, comparing fractions will become second nature!
Latest Posts
Latest Posts
-
Convert 625 Into A Fraction
Sep 14, 2025
-
Adding And Subtracting With Money
Sep 14, 2025
-
10 000 Psi To Bar
Sep 14, 2025
-
Is 1 8 Bigger Than 5 32
Sep 14, 2025
-
What Was 30 Weeks Ago
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Greater Than 3/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.