Is 2/5 Greater Than 3/8
saludintensiva
Sep 19, 2025 · 5 min read
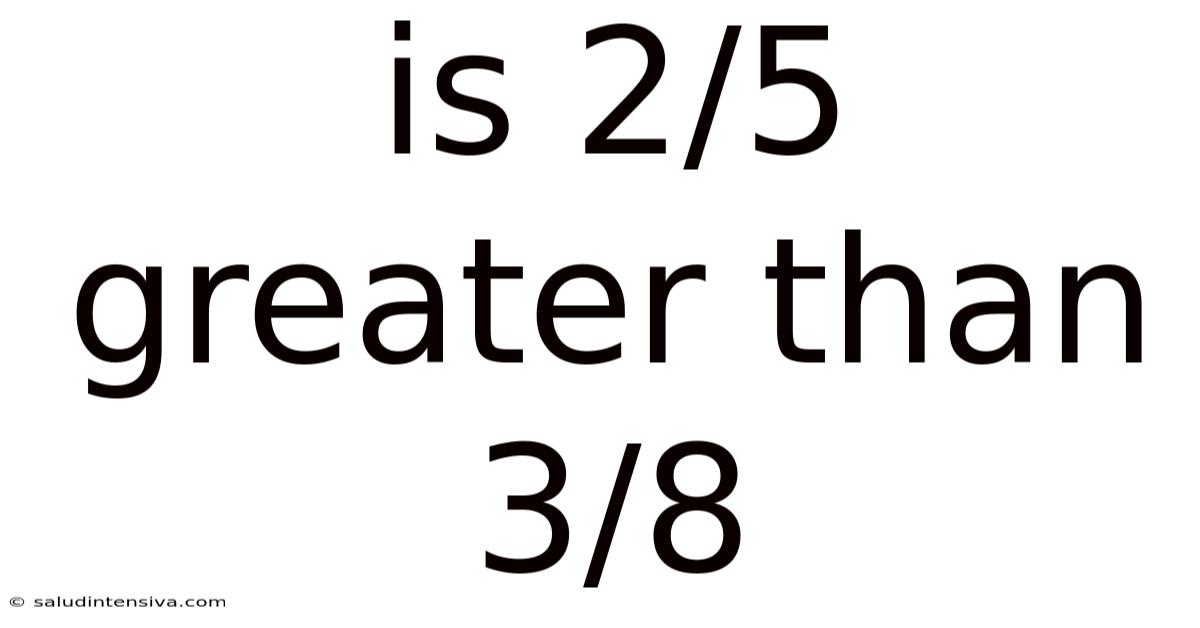
Table of Contents
Is 2/5 Greater Than 3/8? A Comprehensive Exploration of Fraction Comparison
This article explores the question: "Is 2/5 greater than 3/8?". While the answer might seem simple at first glance, delving into the comparison provides a valuable opportunity to understand fundamental concepts in fractions, including equivalent fractions, decimal conversion, and visual representation. This knowledge is crucial for various mathematical applications and everyday problem-solving. We'll explore multiple methods to definitively answer this question and solidify your understanding of fraction comparison.
Introduction to Fractions
Before comparing 2/5 and 3/8, let's quickly review the basics of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
For example, in the fraction 2/5, the numerator is 2 and the denominator is 5. This means we have 2 parts out of a total of 5 equal parts. Similarly, 3/8 represents 3 parts out of a total of 8 equal parts.
Method 1: Finding a Common Denominator
One of the most common methods for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators (5 and 8 in this case). The least common multiple (LCM) is the smallest such number. The LCM of 5 and 8 is 40.
Now, we convert both fractions to equivalent fractions with a denominator of 40:
-
2/5: To get a denominator of 40, we multiply both the numerator and the denominator by 8 (40/5 = 8): (2 x 8) / (5 x 8) = 16/40
-
3/8: To get a denominator of 40, we multiply both the numerator and the denominator by 5 (40/8 = 5): (3 x 5) / (8 x 5) = 15/40
Now that both fractions have the same denominator, we can easily compare them. Since 16/40 > 15/40, we conclude that 2/5 is greater than 3/8.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This involves dividing the numerator by the denominator:
-
2/5: 2 ÷ 5 = 0.4
-
3/8: 3 ÷ 8 = 0.375
Comparing the decimal values, 0.4 > 0.375, confirming that 2/5 is greater than 3/8. This method is particularly useful when dealing with more complex fractions or when using a calculator.
Method 3: Visual Representation
Visualizing fractions can be helpful, especially for beginners. We can represent 2/5 and 3/8 using diagrams:
Imagine a rectangle divided into 5 equal parts. Shading 2 of these parts represents 2/5. Now, imagine another rectangle of the same size divided into 8 equal parts. Shading 3 of these parts represents 3/8. By visually comparing the shaded areas, it becomes apparent that the shaded area representing 2/5 is larger than the shaded area representing 3/8. This confirms that 2/5 is greater than 3/8.
While this method is intuitive for smaller fractions, it becomes less practical for larger or more complex fractions.
Method 4: Cross-Multiplication
Cross-multiplication offers a more concise way to compare two fractions. We multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa. Then, we compare the products:
-
2/5 and 3/8
-
(2 x 8) = 16
-
(3 x 5) = 15
Since 16 > 15, we conclude that 2/5 is greater than 3/8. This method is efficient and avoids the need to find a common denominator.
A Deeper Dive: Understanding Fraction Magnitude
The comparison between 2/5 and 3/8 highlights the importance of understanding the relationship between the numerator and the denominator in determining the magnitude of a fraction. A larger numerator, relative to the denominator, indicates a larger fraction. However, simply comparing numerators or denominators individually is insufficient when comparing fractions with different denominators. The methods described above provide structured approaches to accurately compare fractions with different denominators.
Frequently Asked Questions (FAQ)
Q: Can I always use the common denominator method to compare fractions?
A: Yes, the common denominator method is a universally applicable approach to comparing fractions. While other methods might be quicker in certain scenarios, the common denominator method provides a reliable and easily understandable process for any fraction comparison.
Q: Is converting to decimals always the best method?
A: While converting to decimals is efficient and often yields a clear comparison, it can sometimes lead to recurring decimals (decimals that go on forever without repeating), making precise comparisons challenging. The common denominator method or cross-multiplication avoids this issue.
Q: What if I have more than two fractions to compare?
A: For multiple fractions, you can still use the common denominator method. Find the least common multiple of all the denominators and convert all fractions to equivalent fractions with that common denominator. Then, compare the numerators to determine the order of the fractions from smallest to largest.
Q: Are there any online tools to help compare fractions?
A: Yes, many online calculators and educational websites provide tools to compare fractions, convert fractions to decimals, and find common denominators. These tools can be beneficial for checking your work or assisting with more complex fraction comparisons.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental skill in mathematics with broad applications. The question, "Is 2/5 greater than 3/8?" serves as a simple yet insightful example of how to approach fraction comparison. Through the common denominator method, decimal conversion, visual representation, and cross-multiplication, we've established definitively that 2/5 is indeed greater than 3/8. Understanding these methods and applying them confidently allows you to tackle more complex fraction problems and develop a deeper understanding of this essential mathematical concept. Remember that the key is to choose the method that you find easiest and most reliable, and to always double-check your work. Practicing these methods will enhance your mathematical abilities and build a solid foundation for future learning.
Latest Posts
Latest Posts
-
0 73 Acres To Square Feet
Sep 19, 2025
-
Compound Interest With Withdrawals Formula
Sep 19, 2025
-
5 1 3 As Decimal
Sep 19, 2025
-
Hcf Of 8 And 20
Sep 19, 2025
-
13 Degrees F To Celsius
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Greater Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.