Is 29 A Rational Number
saludintensiva
Sep 20, 2025 · 6 min read
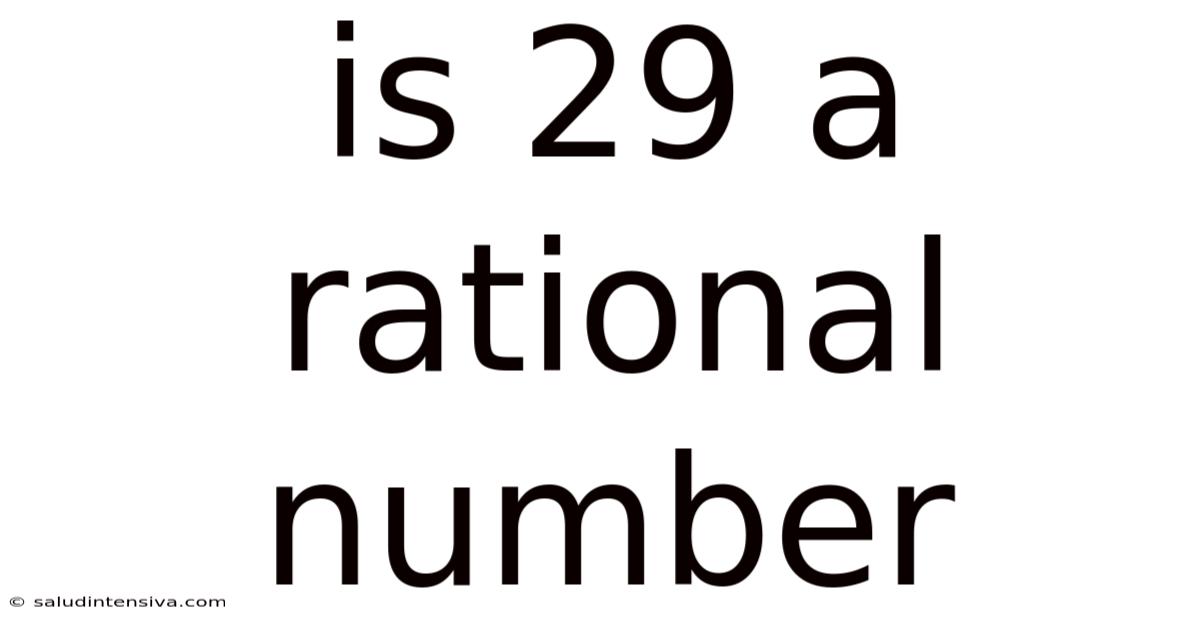
Table of Contents
Is 29 a Rational Number? A Deep Dive into Rational and Irrational Numbers
Is 29 a rational number? The seemingly simple question opens the door to a fascinating exploration of number theory, delving into the fundamental distinctions between rational and irrational numbers. This comprehensive guide will not only answer the question definitively but will also provide a solid understanding of the concepts involved, equipping you with the tools to classify any number you encounter.
Understanding Rational Numbers
A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. The key here is the ability to represent the number as a ratio of two whole numbers. This seemingly simple definition encompasses a vast range of numbers. Think about it:
-
Integers: All whole numbers, both positive and negative (…-3, -2, -1, 0, 1, 2, 3…), are rational numbers. For example, 5 can be expressed as 5/1, -2 as -2/1, and 0 as 0/1.
-
Fractions: Any fraction, whether proper (numerator smaller than denominator) or improper (numerator larger than or equal to the denominator), is a rational number. Examples include 1/2, 3/4, 7/3, and -5/8.
-
Terminating Decimals: Decimals that end after a finite number of digits are rational. For example, 0.75 (which is 3/4), 0.25 (which is 1/4), and 2.375 (which is 19/8) are all rational.
-
Repeating Decimals: Decimals that have a pattern of digits that repeats infinitely are also rational. For example, 0.333… (which is 1/3), 0.142857142857… (which is 1/7), and 0.1666… (which is 1/6) are all rational numbers, even though their decimal representation goes on forever. The repeating pattern allows them to be expressed as a fraction.
Understanding Irrational Numbers
In contrast to rational numbers, irrational numbers cannot be expressed as a fraction p/q, where p and q are integers, and q is not zero. Their decimal representation is non-terminating and non-repeating. This means that the digits after the decimal point continue infinitely without any discernible pattern.
Famous examples of irrational numbers include:
-
π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159... The digits continue infinitely without repeating.
-
e (Euler's number): The base of the natural logarithm, approximately 2.71828... Like π, its decimal representation is infinite and non-repeating.
-
√2 (the square root of 2): This is the number that, when multiplied by itself, equals 2. Its decimal representation is approximately 1.41421... It's impossible to express √2 as a fraction of two integers.
Is 29 a Rational Number? The Definitive Answer
Now, let's return to our initial question: Is 29 a rational number? The answer is a resounding yes.
29 is an integer, and all integers are rational numbers. We can easily express 29 as a fraction: 29/1. This satisfies the definition of a rational number perfectly: it's a ratio of two integers (29 and 1), with the denominator not equal to zero.
Therefore, there's no ambiguity; 29 is unequivocally a rational number.
Proof by Contradiction: Demonstrating the Irrationality of Other Numbers
While proving that a number is rational is often straightforward (simply express it as a fraction), demonstrating that a number is irrational can be more challenging. One common technique is proof by contradiction. Let's illustrate this with a classic example: proving the irrationality of √2.
1. Assume √2 is rational: This is our starting assumption, which we will attempt to contradict. If √2 is rational, it can be expressed as a fraction a/b, where a and b are integers, b ≠ 0, and a and b have no common factors (the fraction is in its simplest form).
2. Square both sides: Squaring both sides of the equation √2 = a/b, we get 2 = a²/b².
3. Rearrange the equation: Rearranging, we have 2*b² = a². This means that a² is an even number (because it's equal to 2 times another integer).
4. Deduce that a is even: If a² is even, then a must also be even. This is because the square of an odd number is always odd. So, we can express a as 2k, where k is another integer.
5. Substitute and simplify: Substituting a = 2k into the equation 2b² = a², we get 2b² = (2k)² = 4k².
6. Simplify further: Dividing both sides by 2, we get b² = 2*k². This shows that b² is also an even number.
7. Deduce that b is even: Following the same logic as before, if b² is even, then b must also be even.
8. Contradiction: We've now shown that both a and b are even numbers. This contradicts our initial assumption that a and b have no common factors (because they both share a common factor of 2).
9. Conclusion: Since our initial assumption leads to a contradiction, the assumption must be false. Therefore, √2 cannot be expressed as a fraction of two integers, and it is irrational.
The Significance of Rational and Irrational Numbers
The distinction between rational and irrational numbers is fundamental in mathematics. It impacts various areas, including:
-
Geometry: Irrational numbers like π and √2 frequently appear in geometric calculations, illustrating the inherent limitations of representing certain measurements using only fractions.
-
Calculus: The concepts of limits and continuity rely heavily on the understanding of both rational and irrational numbers.
-
Algebra: Solving equations and working with different number systems requires a strong grasp of the properties of rational and irrational numbers.
-
Computer Science: Representing and manipulating numbers within computer systems involves dealing with the finite precision limitations, requiring careful consideration of rational and irrational number representations.
Frequently Asked Questions (FAQ)
Q: Can a rational number be expressed in more than one way as a fraction?
A: Yes, absolutely. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. However, all these fractions represent the same rational number. We often simplify fractions to their lowest terms to avoid redundancy.
Q: How can I tell if a decimal is rational or irrational just by looking at it?
A: If the decimal terminates (ends) or has a repeating pattern of digits, it's rational. If it continues infinitely without a repeating pattern, it's irrational. However, determining whether a decimal is truly irrational often requires advanced mathematical techniques.
Q: Are all real numbers either rational or irrational?
A: Yes, the set of real numbers comprises all rational and irrational numbers. This means there are no numbers that are neither rational nor irrational. The set of real numbers encompasses all numbers on the number line.
Conclusion
In conclusion, 29 is definitively a rational number because it can be expressed as the fraction 29/1. Understanding the distinction between rational and irrational numbers is crucial for a deep appreciation of mathematics. This article not only answered the specific question but also provided a broader context, equipping you with the knowledge and tools to classify numbers and understand their properties in various mathematical domains. The exploration of irrational numbers, illustrated through the proof by contradiction for √2, highlights the elegance and rigor of mathematical reasoning. The concepts discussed here are fundamental building blocks for further exploration in more advanced mathematical studies.
Latest Posts
Latest Posts
-
The Square Root Of 30
Sep 20, 2025
-
Best 5 Card Plo Calculator
Sep 20, 2025
-
Meter Chart Smallest To Largest
Sep 20, 2025
-
52 60 As A Percentage
Sep 20, 2025
-
How To Find Diagonal Length
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 29 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.