Is 3/4 Greater Than 2/3
saludintensiva
Sep 15, 2025 · 6 min read
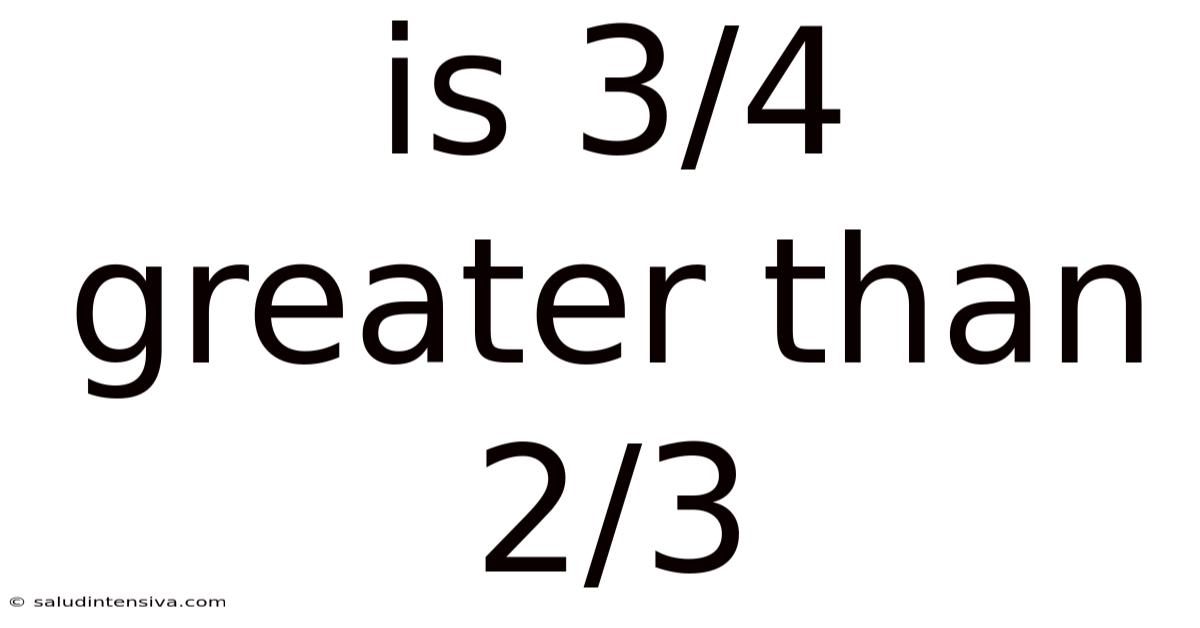
Table of Contents
Is 3/4 Greater Than 2/3? A Deep Dive into Fraction Comparison
Are you struggling to compare fractions? Determining whether 3/4 is greater than 2/3 might seem simple at first glance, but understanding the underlying principles is crucial for mastering fractions. This comprehensive guide will not only answer the question definitively but also equip you with the tools to confidently compare any two fractions. We'll explore various methods, delve into the underlying mathematical concepts, and address common misconceptions. By the end, you'll have a solid grasp of fraction comparison and be able to tackle similar problems with ease.
Understanding Fractions: A Quick Recap
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) tells us we have 3 parts, and the denominator (4) tells us the whole is divided into 4 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most straightforward method for comparing fractions. The goal is to rewrite both fractions so they have the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 3/4 and 2/3, we need to find the least common multiple (LCM) of 4 and 3. The LCM is the smallest number that both 4 and 3 divide into evenly. In this case, the LCM of 4 and 3 is 12.
Now, we rewrite each fraction with a denominator of 12:
- 3/4: To get a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
- 2/3: To get a denominator of 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
Now the comparison is simple: 9/12 > 8/12. Therefore, 3/4 > 2/3.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This allows for a direct numerical comparison.
To convert a fraction to a decimal, we divide the numerator by the denominator:
- 3/4: 3 ÷ 4 = 0.75
- 2/3: 2 ÷ 3 ≈ 0.6667 (This is a repeating decimal)
Comparing the decimal values, we see that 0.75 > 0.6667. Therefore, 3/4 > 2/3.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially for beginners. Imagine two identical pizzas.
- For 3/4, divide the pizza into 4 equal slices and shade 3 of them.
- For 2/3, divide the pizza into 3 equal slices and shade 2 of them.
By visually comparing the shaded areas, it's clear that 3/4 of the pizza is larger than 2/3 of the pizza. This provides a concrete, intuitive understanding of the comparison.
Method 4: Cross-Multiplication
This method is less intuitive but efficient for comparing fractions. We cross-multiply the numerators and denominators:
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (3): 3 x 3 = 9
- Multiply the numerator of the second fraction (2) by the denominator of the first fraction (4): 2 x 4 = 8
Compare the results: 9 > 8. Since the result of the first multiplication is greater, the first fraction (3/4) is greater. Therefore, 3/4 > 2/3.
The Importance of Understanding the Methods
While the answer, 3/4 > 2/3, is straightforward, the different methods highlight crucial concepts in mathematics. Understanding each method provides a deeper understanding of fractions and allows you to adapt your approach depending on the complexity of the fractions being compared. The common denominator method reinforces the concept of equivalent fractions, while decimal conversion highlights the relationship between fractions and decimals. Visual representation provides an intuitive understanding, and cross-multiplication offers a quick algebraic approach.
Addressing Common Misconceptions
Several misconceptions can arise when comparing fractions. Let's address a few common ones:
- Focusing solely on numerators: Simply comparing numerators (3 vs. 2) is incorrect when the denominators are different. The size of the parts (represented by the denominator) matters significantly.
- Incorrectly applying cross-multiplication: Remember to compare the products after cross-multiplication; the larger product corresponds to the larger fraction.
- Rounding errors: When converting to decimals, be mindful of rounding errors, especially with repeating decimals. Carry out the division to enough decimal places to ensure accuracy.
Beyond the Basics: Extending Your Knowledge
The ability to compare fractions is a fundamental building block for more advanced mathematical concepts. Here's how this skill extends:
- Solving inequalities: Comparing fractions is crucial for solving inequalities involving fractions.
- Working with mixed numbers: The same principles apply when comparing mixed numbers (a whole number and a fraction). Convert mixed numbers to improper fractions before applying any of the comparison methods.
- Algebraic manipulation: Many algebraic equations involve fractions, and comparing fractions helps in solving and simplifying them.
- Data analysis: In statistics and data analysis, understanding and comparing fractions is essential for interpreting data and making informed decisions.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to compare fractions?
A: Yes, you can use a calculator to convert fractions to decimals and then compare the decimal values. However, understanding the underlying methods is crucial for developing a strong mathematical foundation.
Q: What if the denominators are very large numbers?
A: Finding the LCM of large numbers can be time-consuming. In such cases, converting to decimals is often a more efficient approach. You can also use prime factorization to find the LCM more easily.
Q: Why is finding a common denominator so important?
A: Finding a common denominator allows you to express both fractions with the same unit of measurement. This makes direct comparison of the numerators possible and straightforward.
Q: Are there other methods to compare fractions besides the ones mentioned?
A: While the methods described are the most common and widely used, there are other less frequently used methods, such as using fraction bars for visual comparison or using the concept of reciprocal for comparison when one fraction is clearly larger or smaller than the other.
Conclusion
Comparing fractions, such as determining whether 3/4 is greater than 2/3, is a fundamental skill in mathematics. Understanding the different methods—finding a common denominator, converting to decimals, visual representation, and cross-multiplication—provides a robust understanding of the underlying concepts. Mastering these methods will not only allow you to accurately compare fractions but also build a solid foundation for more advanced mathematical concepts. Remember to practice regularly, address any misconceptions you might have, and explore the different methods to find the approach that best suits your learning style. With consistent effort, you'll confidently conquer any fraction comparison challenge.
Latest Posts
Latest Posts
-
Square Root Of 1 2
Sep 15, 2025
-
Is 9 Prime Or Composite
Sep 15, 2025
-
15 20 As A Percent
Sep 15, 2025
-
All The Factors Of 24
Sep 15, 2025
-
Is 1 3 Bigger Than 1 4
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.