Is 3/6 Equal To 1/2
saludintensiva
Sep 22, 2025 · 6 min read
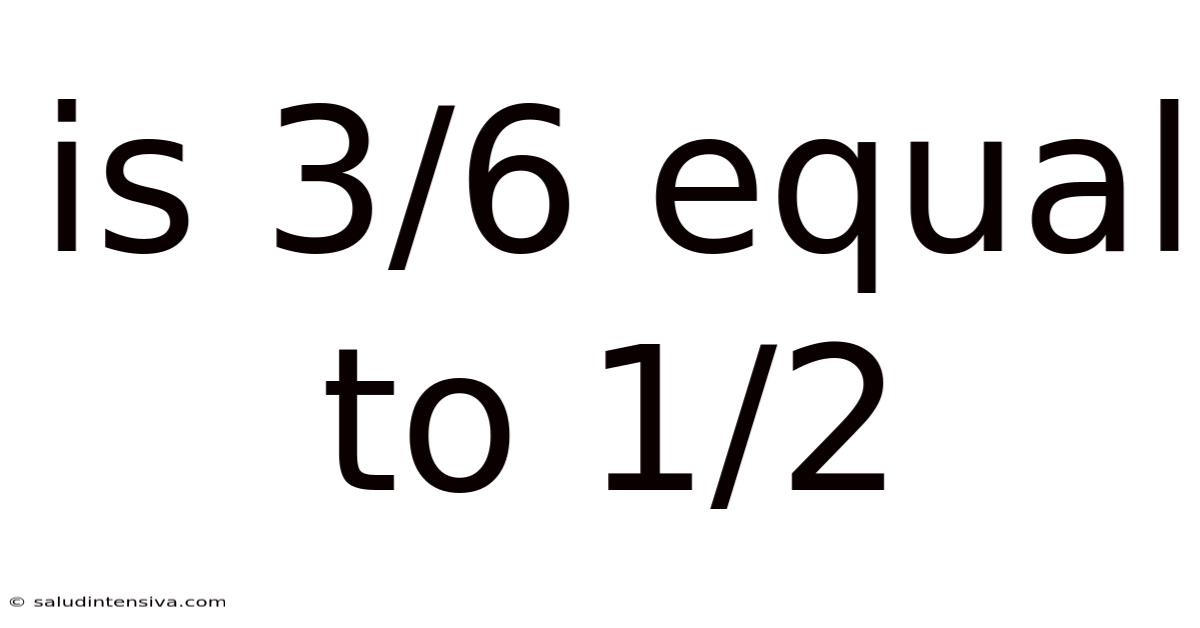
Table of Contents
Is 3/6 Equal to 1/2? A Deep Dive into Fraction Equivalence
Are you struggling with fractions? Many find them confusing, but understanding them is crucial for various aspects of life, from baking to advanced mathematics. One common question that arises is: Is 3/6 equal to 1/2? The short answer is yes, and this article will delve into why, exploring the concept of fraction equivalence, simplifying fractions, and providing practical examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions.
Understanding Fractions: The Building Blocks
Before diving into the equivalence of 3/6 and 1/2, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key numbers:
- Numerator: The top number, indicating how many parts you have.
- Denominator: The bottom number, showing the total number of equal parts the whole is divided into.
For example, in the fraction 3/6, 3 is the numerator and 6 is the denominator. This means we have 3 parts out of a total of 6 equal parts.
Exploring Fraction Equivalence: Why 3/6 = 1/2
The fundamental principle behind fraction equivalence is that you can multiply or divide both the numerator and the denominator by the same number (excluding zero) without changing the value of the fraction. This is because you're essentially scaling the fraction up or down proportionally.
Let's apply this principle to our question: Is 3/6 equal to 1/2?
To determine if two fractions are equivalent, we can simplify one or both to their simplest form. Simplifying a fraction means reducing it to its smallest equivalent fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 3 and 6 is 3. Therefore, we can simplify 3/6 by dividing both the numerator and denominator by 3:
3 ÷ 3 / 6 ÷ 3 = 1/2
This shows that 3/6 simplifies to 1/2. They represent the same proportion or part of a whole. Imagine a pizza cut into six slices. Eating three slices (3/6) is the same as eating half the pizza (1/2).
Visualizing Fraction Equivalence: A Practical Approach
Visual representations can make understanding fraction equivalence much easier. Consider these examples:
-
Using shapes: Draw a circle and divide it into six equal parts. Shade three of those parts. Now draw another circle and divide it into two equal parts. Shade one part. Visually, you'll see that the shaded areas are the same size, demonstrating that 3/6 and 1/2 represent the same portion of the whole.
-
Using objects: Imagine you have six candies. Taking three candies (3/6) is the same as taking half (1/2) of the total candies.
-
Using a number line: A number line can also be used. Mark 0 and 1 on the number line. Divide the space between 0 and 1 into six equal parts. The third mark represents 3/6. Now divide the space between 0 and 1 into two equal parts. The first mark represents 1/2. Both marks will fall on the same point on the number line, confirming their equivalence.
Simplifying Fractions: A Step-by-Step Guide
Simplifying fractions is a crucial skill in mathematics. Here's a step-by-step guide:
-
Find the Greatest Common Divisor (GCD): The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. You can find the GCD using various methods, including listing factors or using the Euclidean algorithm (for larger numbers).
-
Divide the Numerator and Denominator by the GCD: Once you've found the GCD, divide both the numerator and the denominator by this number. The resulting fraction will be the simplified form.
Example: Simplify the fraction 12/18
-
Find the GCD: The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The GCD is 6.
-
Divide: 12 ÷ 6 / 18 ÷ 6 = 2/3
Therefore, the simplified form of 12/18 is 2/3.
Beyond 3/6 and 1/2: More Examples of Equivalent Fractions
The concept of equivalent fractions extends far beyond the simple example of 3/6 and 1/2. Here are a few more examples:
- 2/4 = 1/2 (GCD is 2)
- 4/8 = 1/2 (GCD is 4)
- 5/10 = 1/2 (GCD is 5)
- 6/12 = 1/2 (GCD is 6)
- 10/20 = 1/2 (GCD is 10)
Notice a pattern? All these fractions simplify to 1/2. This demonstrates that there are infinitely many fractions equivalent to 1/2.
Addressing Common Misconceptions
A common misconception is that simplifying a fraction changes its value. This is incorrect. Simplifying a fraction merely represents the same value in a more concise form. It's like expressing the same idea in fewer words – the meaning remains unchanged.
Another misconception is assuming that only fractions with a denominator of 2 can be equal to 1/2. As demonstrated above, numerous fractions with different denominators can be equivalent to 1/2.
The Importance of Fraction Equivalence in Real-World Applications
Understanding fraction equivalence is essential in various real-world applications, including:
-
Cooking and Baking: Recipes often require adjustments based on the number of servings. Knowing how to work with equivalent fractions allows for accurate scaling of ingredients.
-
Construction and Engineering: Precise measurements are crucial in these fields. Fractions are used extensively, and understanding their equivalence ensures accuracy.
-
Finance and Budgeting: Calculating percentages, interest rates, and proportions often involves working with fractions.
-
Data Analysis: Representing and interpreting data frequently involves the use of fractions and their equivalent forms.
Frequently Asked Questions (FAQ)
Q: How can I tell if two fractions are equivalent without simplifying?
A: You can cross-multiply. If the product of the numerator of one fraction and the denominator of the other equals the product of the numerator of the second fraction and the denominator of the first, then the fractions are equivalent. For example, for 3/6 and 1/2: (3 x 2) = (6 x 1) = 6. Therefore, they are equivalent.
Q: Is there a limit to the number of equivalent fractions for a given fraction?
A: No, there are infinitely many equivalent fractions for any given fraction.
Q: What if I have fractions with different denominators that don't simplify to the same fraction? How do I compare them?
A: You need to find a common denominator (a number that is a multiple of both denominators) and then convert both fractions to equivalent fractions with that common denominator. Once they have the same denominator, you can easily compare their numerators.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. It provides a clearer representation of the value and helps in performing calculations more efficiently. It also ensures consistency and avoids unnecessary complexity.
Conclusion: Mastering Fraction Equivalence
In conclusion, 3/6 is indeed equal to 1/2. This fundamental concept of fraction equivalence is built upon the principle of proportionally scaling the numerator and denominator. Understanding this concept, along with the ability to simplify fractions, is crucial for success in mathematics and numerous real-world applications. By mastering fraction equivalence, you'll build a strong foundation for more advanced mathematical concepts and improve your problem-solving skills in various contexts. Remember the visual methods, practice simplifying fractions regularly, and don't hesitate to explore different examples to further solidify your understanding.
Latest Posts
Latest Posts
-
30 Days From April 16
Sep 22, 2025
-
24 Tenths As A Decimal
Sep 22, 2025
-
100 Dollars 20 Percent Off
Sep 22, 2025
-
Six Hundred And Eight Thousandths
Sep 22, 2025
-
3 X 4 2 27
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 3/6 Equal To 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.