Is 3/9 Equivalent To 1/3
saludintensiva
Sep 13, 2025 · 6 min read
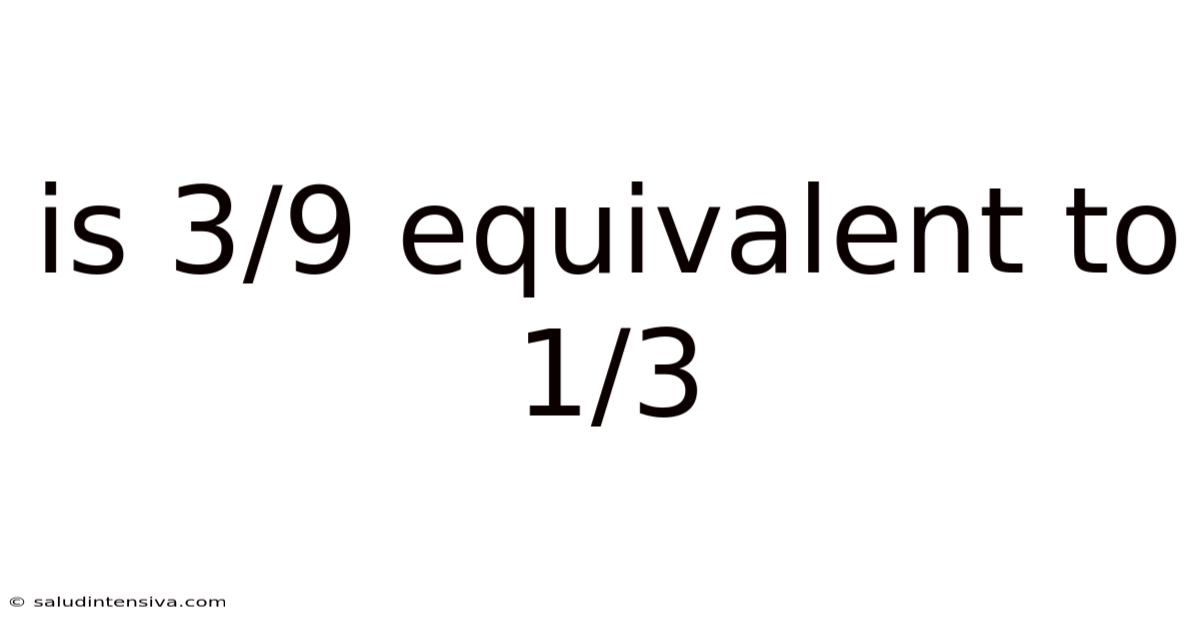
Table of Contents
Is 3/9 Equivalent to 1/3? A Deep Dive into Fraction Equivalence
Are you struggling with fractions? Understanding fraction equivalence is a fundamental concept in mathematics, crucial for success in higher-level math and everyday problem-solving. This article will thoroughly explore the question: Is 3/9 equivalent to 1/3? We'll not only answer this question definitively but also delve into the underlying principles of fraction equivalence, providing you with the tools to confidently tackle similar problems. We’ll cover various methods for determining equivalence, explore the mathematical reasoning behind it, and address common misconceptions.
Understanding Fractions: A Quick Refresher
Before we dive into the equivalence of 3/9 and 1/3, let's revisit the basic components of a fraction. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 3/9, 3 is the numerator and 9 is the denominator. This means we have 3 parts out of a total of 9 equal parts.
Methods for Determining Fraction Equivalence
Several methods can be used to determine if two fractions are equivalent. Let's explore the most common ones:
1. Simplifying Fractions:
This involves reducing a fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's simplify 3/9:
- Find the GCD of 3 and 9. The GCD of 3 and 9 is 3.
- Divide both the numerator and the denominator by the GCD: 3 ÷ 3 = 1 and 9 ÷ 3 = 3.
Therefore, the simplified form of 3/9 is 1/3. Since simplifying 3/9 gives us 1/3, we can definitively say that 3/9 is equivalent to 1/3.
2. Cross-Multiplication:
This method involves multiplying the numerator of one fraction by the denominator of the other fraction, and vice versa. If the products are equal, the fractions are equivalent.
Let's apply this method to 3/9 and 1/3:
- Multiply the numerator of 3/9 (which is 3) by the denominator of 1/3 (which is 3): 3 x 3 = 9
- Multiply the denominator of 3/9 (which is 9) by the numerator of 1/3 (which is 1): 9 x 1 = 9
Since both products are equal (9 = 9), the fractions 3/9 and 1/3 are equivalent.
3. Visual Representation:
Visual aids can help solidify the understanding of fraction equivalence. Imagine a pizza cut into 9 slices. If you take 3 slices, you have 3/9 of the pizza. Now, imagine the same pizza cut into 3 larger slices. Taking one of these larger slices represents 1/3 of the pizza. Visually, you can see that 3/9 and 1/3 represent the same amount of pizza.
The Mathematical Reasoning Behind Fraction Equivalence
The concept of fraction equivalence stems from the fundamental property of division. When we simplify a fraction, we are essentially dividing both the numerator and the denominator by the same number. This operation does not change the value of the fraction; it only changes its representation. Think of it like this: if you divide a cake into 9 equal pieces and take 3, it’s the same as dividing the cake into 3 equal pieces and taking 1.
Addressing Common Misconceptions
Several common misconceptions surround fraction equivalence. Let’s clarify them:
- Misconception 1: Only fractions with the same denominator are equivalent. This is incorrect. Fractions with different denominators can be equivalent, as demonstrated by the example of 3/9 and 1/3.
- Misconception 2: Adding the same number to the numerator and denominator makes equivalent fractions. This is also incorrect. For example, adding 1 to both the numerator and denominator of 1/3 (resulting in 2/4) gives a different value. Only multiplying or dividing both the numerator and denominator by the same number preserves the fraction's value.
- Misconception 3: Larger numbers mean a larger fraction. The size of a fraction is determined by the ratio of the numerator to the denominator, not the absolute size of the numbers. For example, 1/2 is greater than 1/4, even though the numerator and denominator in 1/4 are smaller.
Practical Applications of Fraction Equivalence
Understanding fraction equivalence is not just a theoretical exercise. It has numerous practical applications in various fields:
- Cooking and Baking: Recipes often require adjusting ingredient quantities. Fraction equivalence helps in accurately scaling up or down recipes.
- Construction and Engineering: Accurate measurements are crucial in these fields. Fraction equivalence ensures precise calculations.
- Finance and Accounting: Dealing with percentages and proportions often involves working with fractions.
- Data Analysis: Representing and interpreting data frequently involves working with fractions and percentages.
Expanding the Concept: Equivalent Fractions and Ratios
The concept of equivalent fractions is closely related to the concept of equivalent ratios. A ratio is a comparison of two quantities. For example, the ratio 3:9 is equivalent to the ratio 1:3. The equivalence of fractions and ratios highlights the interconnectedness of these mathematical concepts.
Further Exploration: Working with Mixed Numbers and Improper Fractions
The principles of fraction equivalence also extend to mixed numbers (a whole number and a fraction) and improper fractions (where the numerator is greater than or equal to the denominator). For example, the mixed number 1 2/6 is equivalent to the improper fraction 8/6, which simplifies to 4/3. Mastering these conversions strengthens your overall understanding of fractions.
Frequently Asked Questions (FAQ)
- Q: Can any fraction be simplified? A: Not all fractions can be simplified. Fractions where the numerator and denominator have a GCD of 1 are already in their simplest form (e.g., 2/5).
- Q: Is there a limit to the number of equivalent fractions a given fraction can have? A: No, there is an infinite number of equivalent fractions for any given fraction, except for 0/n (where n is any integer).
- Q: How can I practice my skills in determining fraction equivalence? A: Practice is key! Work through various exercises that involve simplifying fractions, cross-multiplication, and visual representations. Online resources and textbooks offer numerous practice problems.
Conclusion: Mastering the Fundamentals of Fractions
In conclusion, 3/9 is indeed equivalent to 1/3. Understanding this equivalence is a cornerstone of mathematical proficiency. Through simplification, cross-multiplication, or visual representation, we can confidently determine the equivalence of fractions. This fundamental skill is not only essential for academic success but also for navigating numerous real-world scenarios. By mastering the principles discussed in this article, you'll be well-equipped to tackle more complex fractional problems with greater confidence and understanding. Remember that consistent practice and a clear understanding of the underlying mathematical principles are key to mastering fractions and achieving mathematical fluency.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 13
Sep 14, 2025
-
7000 Sq Ft To Acres
Sep 14, 2025
-
Pressure Force And Area Formula
Sep 14, 2025
-
Gcf Of 32 And 45
Sep 14, 2025
-
What Time Is 15 54
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Is 3/9 Equivalent To 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.